本试卷共三道大题,28道小题。满分100分。考试时间120分钟。
一、选择题 (本题共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个。
1. 2020年初,新型冠状病毒引发肺炎疫情。一方有难,八方支援,全国多家医院纷纷选派医护人员驰援武汉。下面是四家医院标志的图案部分,其中是轴对称图形的是

齐鲁医院 华西医院 湘雅医院 协和医院
A B C D
2. 据报道,位于丰台区的北京排水集团槐房再生水厂,是亚洲规模最大的一座全地下再生水厂,日处理污水能力600 000立方米,服务面积137平方公里。将600 000用科学记数法表示为
A. 0.6×105 B. 0.6×106 C. 6×105 D. 6×106
3. 正六边形的每个内角度数为
A. 60° B. 120° C. 135° D.150°
4. 下列几何体的主视图和俯视图完全相同的是
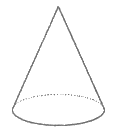
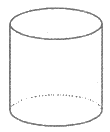
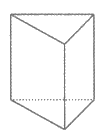
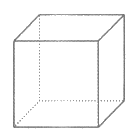
圆锥 圆柱 三棱柱 正方体
A B C D
5. 在数轴上,点A,B分别表示数a,3,点A关于原点O的对称点为点C。如果点C为线段AB的中点,那么a的值为
A. -3 B. -1 C. 1 D. 3
6. 在⊙O中按如下步骤作图:
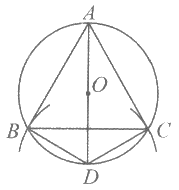
(1)作⊙O的直径AD;
(2)以点D为圆心,DO长为半径画弧,交⊙O于B,C两点;
(3)连接DB,DC,AB,AC,BC。
根据以上作图过程及所作图形,下列四个结论中错误的是
A. ∠ABD=90° B. ∠BAD=∠CBD
C. AD⊥BC D. AC=2CD
7. 某区响应国家提出的垃圾分类的号召,设置了”厨余垃圾”箱、”可回收物”箱、”有害垃圾”箱及”其他垃圾”箱。为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如下表:

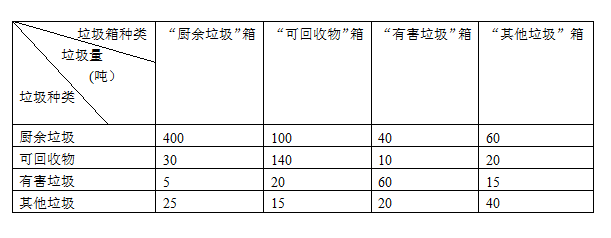 下列三种说法:
下列三种说法:
(1)厨余垃圾投放错误的有400吨
(2)估计可回收物投放正确的概率约为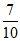
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普
其中正确的个数是
A. 0 B. 1 C. 2 D. 3
8. 图书馆将某一本书和某一个关键词建立联系,规定:当关键词Ai出现在书Bj中时,aij=1,否则aij=0(i,j为正整数)。例如:当关键词A1出现在书B4中时,a14=1,否则a14=0。根据上述规定,某读者去图书馆寻找同时包含关键词A2,A5,A6的书,
则下列相关表述错误的是
A. 当a21+ a51+ a61=3时,选择B1这本书
B. 当a22+ a52+ a62<3时,不选择B2这本书
C. 当a2j,a5j,a6j全是1时,选择Bj这本书
D. 只有当a2j+a5j+a6j=0时,才不能选择Bj这本书
二、填空题(本题共16分,每小题2分)
9. 如果二次根式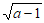 有意义,那么实数a的取值范围是_________。
有意义,那么实数a的取值范围是_________。
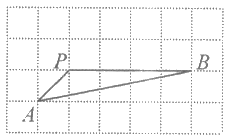
10. 如图所示的网格是正方形网格,则∠PAB+∠PBA=_________°(点A,B,P是网格线交点)。
11. 当m+n=1时,代数式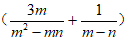 ·
·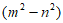 的值为_________。
的值为_________。
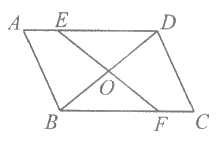
12. 如图,□ABCD中,E为AD上一点,F为BC上一点,EF与对角线BD交于点O,以下三个条件:①BO=DO;②EO=FO;③AE=CF,以其中一个作为题设,余下的两个作为结论组成命题,其中真命题的个数为_________。
13. 如图1,小长方形纸片的长为2,宽为1,将4张这样的小长方形纸片按图2所示的方式不重叠的放在大长方形内,未被覆盖的部分恰好被分割为两个长方形I和Ⅱ,设长方形I和Ⅱ的周长分别为C1和C2,则C1_________C2 (填”>”, “=” 或”<“)。
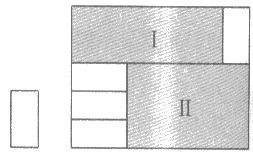
图1 图2
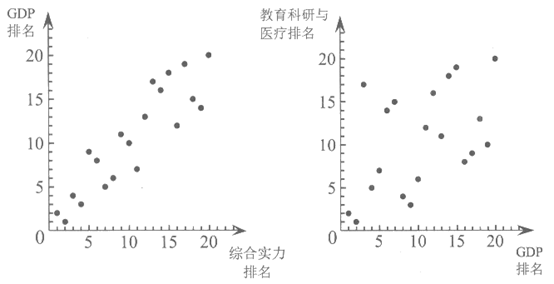
14. 某研究机构发布了《2019年中国城市综合实力排行榜》,其中部分城市的综合实力、GDP和教育科研与医疗的排名情况如图所示,综合实力排名全国第5名的城市,教育科研与医疗排名全国第_________名。
15. 已知函数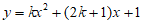 (k为实数)。
(k为实数)。
(1)对于任意实数k,函数图象一定经过点(-2,-1)和点__________;
(2)对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值为__________。
16. 某快递公司的快递件分为甲类件和乙类件,快递员送甲类件每件收入1元,送乙类件每件收入2元。累计工作1小时,只送甲类件,最多可送30件,只送乙类件,最多可送10件;累计工作2小时,只送甲类件,最多可送55件,只送乙类件,最多可送20件;……,经整理形成统计表如下:
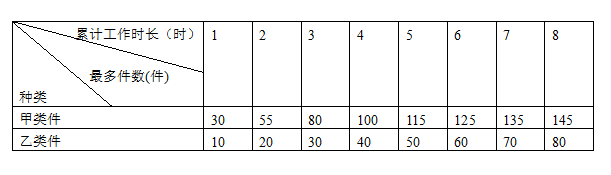
(1)如果快递员一天工作8小时,且只送某一类件,那么他一天的最大收入为________元;
(2)如果快递员一天累计送x小时甲类件,y小时乙类件,且x+y=8,x,y均为正整数,那么他一天的最大收入为_________元。
三、解答题(本题共68分,第17-23题,每小题5分,第24-25题,每小题6分,第26-28题,每小题7分)
17. 计算: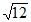 -2cos30°+(3-
-2cos30°+(3-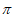 )0+|1-
)0+|1-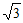 |。
|。
18. 解不等式组: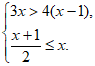
19. 如图,在△ABC中,∠CAB=∠CBA,AD⊥BC于点D,BE⊥AC于点E。
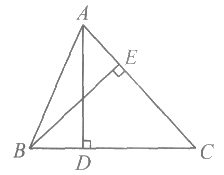
求证:AD=BE。
20. 关于x的一元二次方程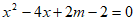 有两个不相等的实数根。
有两个不相等的实数根。
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根。
21. 在平面直角坐标系xOy中,一次函数y=x+4的图象与y轴交于点A,与反比例函数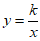 的图象的一个交点为M。
的图象的一个交点为M。
(1)求点A的坐标;
(2)连接OM,如果△MOA的面积等于2,求k的值。
22. 如图,在□ABCD中,AC,BD交于点O,且AO=BO。
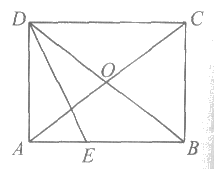
(1)求证:四边形ABCD是矩形;
(2)∠ADB的角平分线DE交AB于点E,当AD=3,tan∠CAB=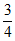 时,求AE的长。
时,求AE的长。
23. 居民人均可支配收入、居民人均消费总支出和恩格尔系数都是反映居民生活水平的指标,其中恩格尔系数指居民家庭中食品支出占消费总支出的比重,恩格尔系数越小,说明食品支出占消费总支出的比重越低,居民家庭越富裕,反之越贫穷。下面是根据从权威机构获得的部分数据绘制的统计图:
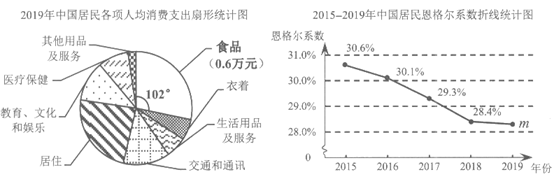
2015-2019年中国居民人均消费总支出和人均可支配收入条形统计图
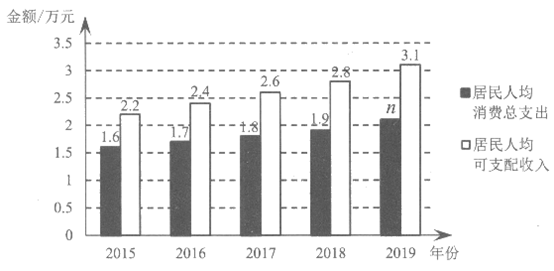
根据以上信息,回答下列问题:
(1)2019年中国居民恩格尔系数m约为_________(精确到0.1%);
(2)2019年中国居民人均消费总支出n约为_______万元(精确到千位);
(3)下面的推断合理的是_______。
①2015-2019年中国居民人均可支配收入和居民人均消费总支出均呈逐年上升的趋势,说明中国居民生活水平逐步提高;
②2015-2019年中国居民恩格尔系数呈逐年下降的趋势,说明中国居民家庭富裕程度越来越高。
24. 在Rt△ABC中,∠A=90°,∠B=22.5°。点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a(a为常数),到点P的距离等于a的所有点组成图形W。点D为线段BC延长线上一点,且点D到点A的距离也等于a。

(1)求直线DA与图形W的公共点个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长。
25. 如图,点C是以O为圆心,AB为直径的半圆上的动点(不与点A,B重合),AB=5cm,过点C作CD⊥AB于点D,E是CD的中点,连接AE并延长交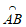 于点F,连接FD。
于点F,连接FD。
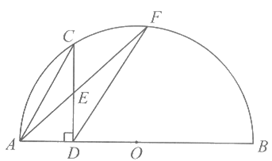
小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究。
下面是小腾的探究过程,请补充完整:
(1)对于点C在 上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如下表:
上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |
在AC,CD,FD的长度这三个量中,确定___________的长度是自变量,____________的长度和____________的长度都是这个自变量的函数:
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当CD>FD时,AC的长度的取值范围为_________。
26. 已知二次函数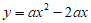 。
。
(1)二次函数图象的对称轴是直线x=_________;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围。
27. 已知∠AOB=120°,点P为射线OA上一动点(不与点O重合),点C为∠AOB内部一点,连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,且点Q恰好落在射线OB上,不与点O重合。
(1)依题意补全图l;
(2)用等式表示∠CPO与∠CQO之间的数量关系,并证明;
(3)连接OC,写出一个OC的值,使得对于任意点P,总有OP+OQ=4,并证明。
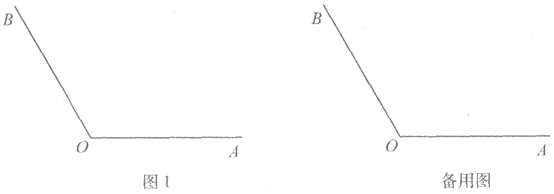
28. 如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆。特别地,当这个圆与角的至少一条边相切时,称这个圆为该角的角内相切圆。
在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上。
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是________;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2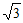 )的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围。
)的圆为∠EOM的角内相切圆,直接写出∠EOM的取值范围。
参考答案
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | C | B | D | B | D | C | D |
二、填空题(本题共16分,每小题2分)
9. a≥1 10. 45 11. 4 12. 3 13. =
14. 3 15. (0,1);0(答案不唯一,m≥-1即可) 16. 160:180
三、解答题(本题共68分,第17-23题,每小题5分,第24-25题,每小题6分,第26-28题,每小题7分)
17. 解:原式=2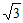 -2×
-2×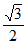 +1+
+1+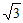 -1, ……3分
-1, ……3分
=2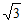 –
–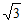 +1+
+1+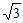 -1, ……4分
-1, ……4分
=2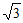 。 ……5分
。 ……5分
18. 解: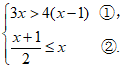
解不等式①得x<4。 ……2分
解不等式②得x≥1。 ……4分

∴ 不等式组的解集为1≤x<4。 ……5分
19. 证明:∵∠CAB=∠CBA,
∴CA=CB。 ……2分
∵AD⊥BC于点D,
BE⊥AC于点E,
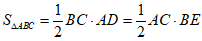 ,
,
∴AD=BE。 ……5分
20. 解:
(1)∵一元二次方程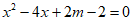 有两个不相等的实数根,
有两个不相等的实数根,
∴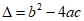 ……1分
……1分
=16-4(2m-2)>0。
解得m<3。 ……2分
(2)当m=1时,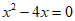 。 ……3分
。 ……3分
解得x1=0,x2=4。 ……5分
21. 解:(1)令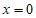 ,
,
∴y=4。
∴A(0,4)。 ……2分
(2)∵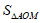 =2,AO=4,
=2,AO=4,
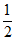 ×AO×|xM|=2,
×AO×|xM|=2,
∴|xM|=1。 ……3分
①当xM=1时,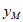 =5。
=5。
如下图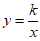 过点(1,5),
过点(1,5),
∴k=5。 ……4分
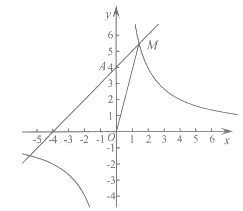
②当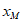 =-1时,
=-1时,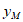 =3。
=3。
如下图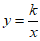 过点(-1,3),
过点(-1,3),
∴k=-3。 ……5分
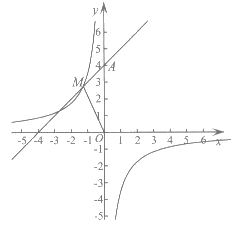
综上所述,k=5或-3。
22. (1)证明:∵□ABCD,
∴AC=2AO,BD=2BO。 ……1分
∵AO=BD,
∴AC=BD。
∴□ABCD为矩形。 …2分
(2)解:过点E作EG⊥BD于点G,
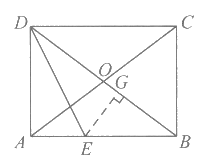
∵DE为∠ADB的角平分线,且∠DAB=90°
∴EG=EA。 ……3分
∵AO=BO,
∴∠CAB=∠ABD。
∵AD=3,tan∠CAB=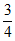 ,
,
∴tan∠CAB=tan∠ABD=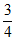 。
。
∴AB=4。
∴sin∠CAB=sin∠ABD=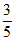 。
。
设AE=x,则BE=4-x,
在△BEG中,∠BGE=90°,
∴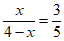 。 …4分
。 …4分
解得AE=x=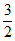 。 ……5分
。 ……5分
23. (1)28.3%; ……1分
(2)2.1; ……3分
(3)①②。 ……5分
24. 解:(1)直线DA与图形W的公共点的个数为1个。 ……1分
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点。
∵到点P的距离等于a的所有点组成图形W。
∴图形W是以点P为圆心,a为半径的圆。
根据题意补全图形:
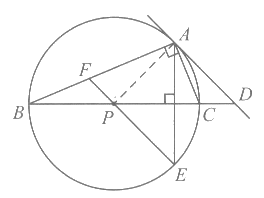 ……2分
……2分
连接AP
∵∠B=22.5°,
∴∠APD=45°。
∵点D到点A的距离也等于a,
∴DA=AP=a。
∴∠D=∠APD=45°。
∴∠PAD=90°。
∴DA⊥PA。
∴DA为⊙P的切线。
∴直线DA与图形W的公共点的个数为1个。 ……3分
(2)∵AP=BP,
∴∠BAP=∠B=22.5°。
∵∠BAC=90°。
∴∠PAC=∠PCA=67.5°。
∴PA=PC=a。
∴点C在⊙P上。 ……4分
∵AE⊥BD交图形W于点E,
∴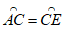 。
。
∴∠DPE=∠APD=45°。
∴∠APE=90°。
∵EP=AP=a=2,
∴AE=2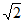 ,∠E=45°。…5分
,∠E=45°。…5分
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°。
∴∠AFE=∠BAE=67.5°。
∴EF=AE=2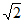 。 ……6分
。 ……6分
25. 解:(1)AC,CD,FD。………………………………………2分
(2)正确画出函数图象:
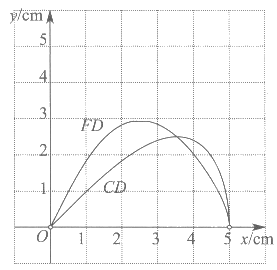
…………………………4分
(3)3.5cm<x<5cm。……………………………………………6分
26. 解:(1)对称轴是直线x=1。………………………………………1分
(2)当a>0时,∵对称轴为x=1,
当x=1时,y有最小值为-a;当x=3时,y有最大值为3a。………………2分
∴3a-(-a)=4。
∴a=1。 …………………………3分
∴二次函数的表达式为: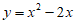 。……………………………………4分
。……………………………………4分
当a<0时,同理可得
y有最大值为-a;y有最小值为3a。
∴-a-3a=4。
∴a=-1。
∴二次函数的表达式为: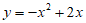 。……………………………5分
。……………………………5分
综上所述,二次函数的表达式为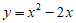 或
或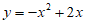 。
。
(3)-1≤t≤2。 ……………………………………………………7分
27. 解:(1)正确补全图1:
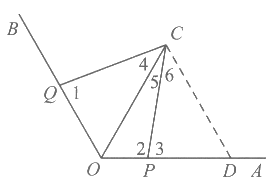 ………………2分
………………2分
(2)∠CQO+∠CPO=180°。……………………………………3分
理由如下:∵四边形内角和360°,
且∠AOB=120°,∠PCQ=60°,
∴∠CQO+∠CPO=∠1+∠2=180°。…………………………4分
(3)OC=4时,对于任意点P,总有OP+OQ=4。 …………………………5分
证明:连接OC,在射线OA上取点D,使得DP=OQ,连接CD。
∴OP+OQ=OP+DP=OD。
∵∠1+∠2=180°,
∵∠2+∠3=180°,
∴∠1=∠3。
∵CP=CQ
∴△CDQ≌△CDP(SAS)。 …………………………………………6分
∴∠4=∠6,OC=CD。
∴∠4+∠5=60°,
∴∠5+∠6=60°。
即∠OCD=60°。
∴△COD是等边三角形。
∴OC=OD=OP+OQ=4。………………………………………7分
28. 解:(1)⊙B,⊙C。……………………………2分
(2)解:如图,
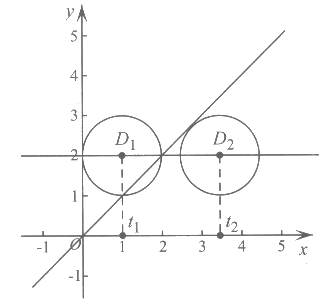
当⊙D1与y轴相切时,t1=1。………………………………………………3分
当⊙D2与y=x相切时,t2=2+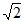 。……………………………………4分
。……………………………………4分
∴t的取值范围是1≤t≤2+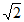 。…………………………………………5分
。…………………………………………5分
(3)60°≤∠EOM<90°。………………………………………………7分
