本试卷共150分。考试时长120分钟。
第一部分 (选择题 共40分)
一、选择题共10题,每题4分,共40分。在每题列出的四个选项中,选出符合题目要求的一项。
1. 已知全集U={0,1,2,3,4,5},集合A={0,1,2},B={5},那么(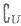 A)UB=
A)UB=
A. {0,1,2} B. {3,4,5} C. {1,4,5} D. {0,1,2,5}
2. 已知三个函数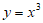 ,
,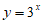 ,
,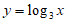 ,则
,则
A. 定义域都为R B. 值域都为R
C. 在其定义域上都是增函数 D. 都是奇函数
3. 平面直角坐标系中,已知点A,B,C的坐标分别为(0,1),(1,0),(4,2),且四边形ABCD为平行四边形,那么D点的坐标为
A. (3,3) B. (-5,1) C. (3,-1) D. (-3,3)
4. 双曲线C: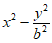 =1的渐近线与直线
=1的渐近线与直线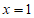 交于A,B两点,且|AB|=4,那么双曲线C的离心率为
交于A,B两点,且|AB|=4,那么双曲线C的离心率为
A. 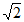 B.
B. 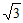 C. 2 D.
C. 2 D.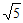
5. 已知函数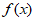 =
=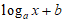 的图象如图所示,那么函数g(x)=ax+b的图象可能为
的图象如图所示,那么函数g(x)=ax+b的图象可能为
 A B C D
A B C D
6. 已知向量a=(0,5),b=(4,-3),c=(-2,-1),那么下列结论正确的是
A. a– b与c为共线向量 B. a – b与c垂直
C. a – b与a的夹角为钝角 D. a – b与b的夹角为锐角
7. 《九章算术》成书于公元一世纪,是中国古代乃至东方的第一部自成体系的数学专著。书中记载这样一个问题”今有宛田,下周三十步,径十六步。问为田几何?”(一步=1.5米)意思是现有扇形田,弧长为45米,直径为24米,那么扇形田的面积为
A. 135平方米 B. 270平方米 C. 540平方米 D. 1080平方米
8. 已知函数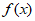 =lnx+ax2,那么”a>0″是”
=lnx+ax2,那么”a>0″是”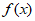 在(0,+
在(0,+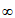 )上为增函数”的
)上为增函数”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 已知一个几何体的三视图如图所示,正(主)视图是由一个半圆弧和一个正方形的三边拼接而成的,俯视图和侧(左)视图分别为一个正方形和一个长方形,那么这个几何体的体积是
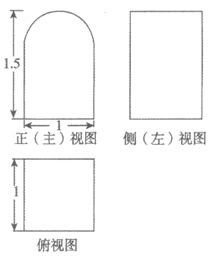
A. 1+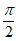 B. 1+
B. 1+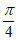 C. 1+
C. 1+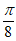 D. 1+
D. 1+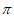
10. 函数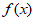 是定义域为R的奇函数,且它的最小正周期是T,已知
是定义域为R的奇函数,且它的最小正周期是T,已知
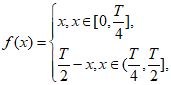 g(x)=
g(x)=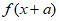 (a
(a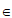 R)。给出下列四个判断:
R)。给出下列四个判断:
①对于给定的正整数n,存在a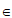 R,使得
R,使得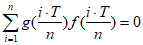 成立;
成立;
②当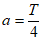 时,对于给定的正整数n,存在k∈R(k≠1),使得
时,对于给定的正整数n,存在k∈R(k≠1),使得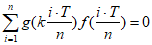 成立;
成立;
③当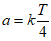 (k
(k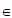 Z)时,函数g(x)+f(x)的图象既有对称轴又有对称中心;
Z)时,函数g(x)+f(x)的图象既有对称轴又有对称中心;
④当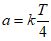 (k
(k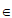 Z)时,g(x)+f(x)的值只有0或
Z)时,g(x)+f(x)的值只有0或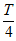 。
。
其中正确判断有
A. 1个 B. 2个 C. 3个 D. 4个
第二部分 (非选择题 共110分)
二、填空题共5题。每题5分,共25分。
11. 复数z=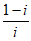 的共轭复数
的共轭复数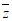 为_________。
为_________。
12. 已知cos2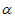 =
=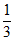 ,则cos2(
,则cos2(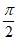 +
+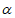 )-2cos2(
)-2cos2(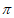 –
–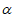 )的值为_________。
)的值为_________。
13. 设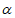 ,
,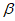 ,
,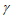 是三个不同的平面,m,n是两条不同的直线,给出下列三个结论:
是三个不同的平面,m,n是两条不同的直线,给出下列三个结论:
①若m⊥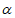 ,n⊥
,n⊥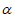 ,则m∥n;②若m⊥
,则m∥n;②若m⊥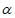 ,m⊥
,m⊥ ,则
,则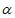 ∥
∥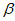 ;③若
;③若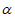 ⊥
⊥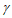 ,
,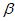 ⊥
⊥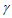 ,则
,则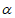 ∥
∥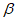 。
。
其中,正确结论的序号为_________。
注:本题给出的结论中,有多个符合题目要求。全部选对得5分,不选或有错选得0分,其他得3分。
14. 从下列四个条件①a=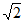 c;②
c;②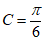 ;③cosB=
;③cosB=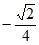 ;④b=
;④b=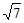 中选出三个条件,能使满足所选条件的△ABC存在且唯一,你选择的三个条件是_________ (填写相应的序号),所选三个条件下的c的值为_________。
中选出三个条件,能使满足所选条件的△ABC存在且唯一,你选择的三个条件是_________ (填写相应的序号),所选三个条件下的c的值为_________。
15. 配件厂计划为某项工程生产一种配件,这种配件每天的需求量是200件。由于生产这种配件时其他生产设备必须停机,并且每次生产时都需要花费5000元的准备费,所以需要周期性生产这种配件,即在一天内生产出这种配件,以满足从这天起连续n天的需求,称n为生产周期(假设这种配件每天产能可以足够大)。配件的存储费为每件每天2元(当天生产出的配件不需要支付存储费,从第二天开始付存储费)。在长期的生产活动中,为使每个生产周期内每天平均的总费用最少,那么生产周期n为________。
三、解答题共6题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题14分)
如图①,四边形ABCD中,AD∥BC,CD⊥BC,BC=CD=1,AD=2,E为AD中点。将△ABE沿BE折起到△A1BE的位置,如图②。

(I)求证:平面A1EB⊥平面A1ED;
(Ⅱ)若∠A1ED=90°,求A1C与平面A1BD所成角的正弦值。
17. (本小题14分)
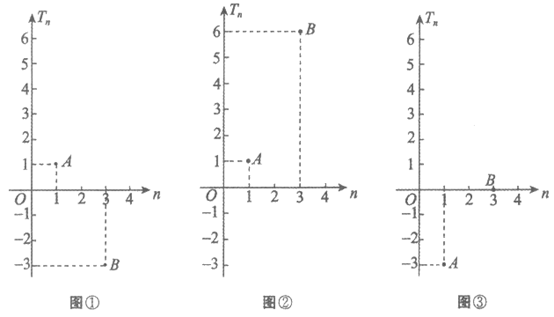
已知{an}为等比数列,其前n项和为Sn,且满足a3=1,S3=3a2+1。{bn}为等差数列,其前n项和为Tn,如图_________,Tn的图象经过A,B两个点。
(I)求Sn;
(Ⅱ)若存在正整数n,使得bn>Sn,求n的最小值。
从图①,图②,图③中选择一个适当的条件,补充在上面问题中并作答。
注:如果选择多个条件分别解答,按第一个解答计分。
18. (本小题14分)
某志愿者服务网站在线招募志愿者,当报名人数超过计划招募人数时,将采用随机抽取的方法招募志愿者,下表记录了A,B,C,D四个项目最终的招募情况,其中有两个数据模糊,记为a,b。
项目 | 计划招募人数 | 报名人数 |
A | 50 | 100 |
B | 60 | a |
C | 80 | b |
D | 160 | 200 |
甲同学报名参加了这四个志愿者服务项目,记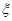 为甲同学最终被招募的项目个数,已知P(
为甲同学最终被招募的项目个数,已知P(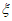 =0)=
=0)=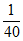 ,P(
,P(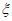 =4)=
=4)=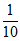 。
。
(I)求甲同学至多获得三个项目招募的概率;
(Ⅱ)求a,b的值;
(Ⅲ)假设有十名报了项目A的志愿者(不包含甲)调整到项目D,试判断E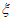 如何变化(结论不要求证明)。
如何变化(结论不要求证明)。
19. (本小题14分)
已知椭圆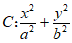 =1(a>b>0)的一个顶点坐标为A(0,-1),离心率为
=1(a>b>0)的一个顶点坐标为A(0,-1),离心率为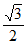 。
。
(I)求椭圆C的方程;
(Ⅱ)若直线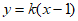 (k≠0)与椭圆C交于不同的两点P,Q,线段PQ的中点为M,点B(1,0),求证:点M不在以AB为直径的圆上。
(k≠0)与椭圆C交于不同的两点P,Q,线段PQ的中点为M,点B(1,0),求证:点M不在以AB为直径的圆上。
20. (本小题15分)
已知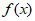 =
=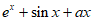 (a∈R)。
(a∈R)。
(I)当a=-2时,求证: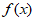 在(-
在(-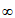 ,0)上单调递减;
,0)上单调递减;
(Ⅱ)若对任意x≥0,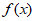 ≥1恒成立,求实数a的取值范围;
≥1恒成立,求实数a的取值范围;
(Ⅲ)若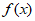 有最小值,请直接给出实数a的取值范围。
有最小值,请直接给出实数a的取值范围。
21. (本小题14分)
设数列:A:a1,a2,…,an,B:b1,b2,…,bn。已知ai,bj∈{0,1}(i=1,2,…,n;j=1,2,…,n),定义n×n数表X(A,B)=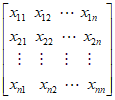 ,其中
,其中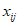 =
=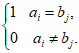
(I)若A:1,1,1,0,B:0,1,0,0,写出X(A,B);
(Ⅱ)若A,B是不同的数列,求证:n×n数表X(A,B)满足”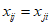 (i=l,2,…,n;j=1,2,…,n;
(i=l,2,…,n;j=1,2,…,n;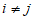 )”的充分必要条件为”ak+bk=1(k=1,2,…,n)”;
)”的充分必要条件为”ak+bk=1(k=1,2,…,n)”;
(Ⅲ)若数列A与B中的1共有n个,求证:n×n数表X(A,B)中1的个数不大于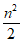 。
。
参考答案
一、选择题(共10小题,每小题4分,共40分)
1. B 2. C 3. A 4. D 5. B
6. B 7. B 8. A 9. C 10. C
二、填空题(共5小题,每小题5分,共25分)
11. -1+i 12. -1
13. ①② 14. ①③④,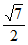 ,或者②③④,
,或者②③④,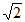
15. 5
三、解答题(共6小题,共85分)
16. (本小题14分)
(I)证明:因为四边形ABCD中,AD//BC,CD⊥BC,BC=1,AD=2,
E为AD中点,
所以BE⊥AD。
故图②中,BE丄A1E,BE⊥DE。
又因为A1E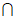 DE=E,A1E,DE
DE=E,A1E,DE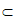 平面A1DE,
平面A1DE,
所以BE丄平面A1DE。
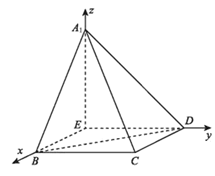
又因为BE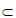 平面A1EB,
平面A1EB,
所以平面A1EB丄平面A1DE。 5分
(II)解:由∠A1ED = 90°得A1E丄DE,
又A1E⊥BE,BE⊥DE,
因此,建立如图所示的空间直角坐标系E-xyz。
由A1E=CD=DE=l,
得A1(0,0,1),B(1,0,0),C(1,1,0),D(0,1,0),
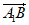 =(1,0,-1),
=(1,0,-1),
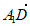 =(0,1,-1),
=(0,1,-1),
设平面A1BD的法向量为n=(x,y,z),
则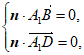 即
即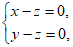
令z=l得x=1,y=l,
所以n=(1,1,1)是平面A1BD的一个法向量。
又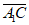 =(1,1,-1),
=(1,1,-1),
设直线A1C与平面A1BD所成角为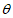 ,
,
所以sin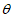 =|cos<n,
=|cos<n,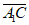 >|=
>|=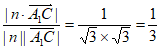 14分
14分
17. (本小题14分)
解:(I)由S3=3a2+1,得a1=2a2,即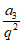 =
=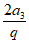 ,
,
因为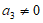 ,所以
,所以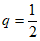 ,
,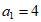 ,
,
所以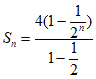 =8
=8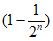 =
=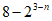 。 6分
。 6分
(II)由图①知:T1=b1=1,T3=-3,可判断d<0,数列{bn}是递减数列;
而{8-23-n}递增,由于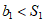 ,所以选择①不满足”存在n,使得bn>Sn“。
,所以选择①不满足”存在n,使得bn>Sn“。
由图②知:T1=b1=1,T3=6,可判断d>0,数列{bn}是递增数列;
由图③知:T1=b1=-3,T3=0,可判断d>0,数列{bn}是递增数列。
所以选择②③均可能满足”存在n,使得bn>Sn“。
第一种情况:
如果选择条件②,即T1=b1=1,T3=6,可得:d=1,bn=n。
当n=1,2,3,4,5,6,7时,bn>Sn不成立,
当n=8时,b8=8,S8=8-23-8<b8,
所以使得bn>Sn成立的n的最小值为8。 14分
第二种情况:
如果选择条件③,即T1=b1=-3,T3=0,可得:d=3,bn=3n-6。
当n=1,2,3,4时,bn>Sn不成立,
当n=5时,b5=9,S5=8-23-5<b5成立,
所以使得bn>Sn成立的n的最小值为5。 14分
18. (本小题14分)
解:因为P(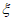 =0)=
=0)=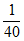 ,所以a>60,且b>80。
,所以a>60,且b>80。
设事件A表示”甲同学被项目A招募”,由题意可知,P(A)=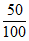 =
=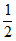 ;
;
设事件B表示”甲同学被项目B招募”,由题意可知,P(B)=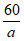 ;
;
设事件C表示”甲同学被项目C招募”,由题意可知,P(C)=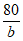 ;
;
设事件D表示”甲同学被项目D招募”,由题意可知,P(D)=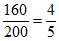 ;
;
(I)由于事件”甲同学至多获得三个项目招募”与事件”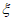 =4″是对立的,
=4″是对立的,
所以甲同学至多获得三个项目招募的概率是1-P(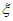 =4)=1-
=4)=1-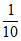 =
=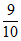 。 4分
。 4分
(II)由题意可知,
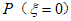 =
=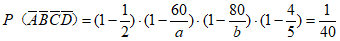 ;
;
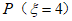 =
=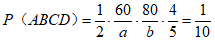 ;
;
解得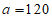 ,
,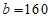 。 12分
。 12分
(III)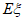 变大。 14分
变大。 14分
19.(本小题14分)
(I)解:由题意可知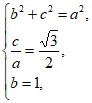
解得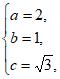
所以椭圆C的方程为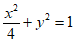 。 4分
。 4分
(II)证明:设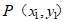 ,
,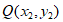 ,
,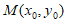 。
。
由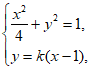 得
得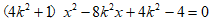 ,
,
所以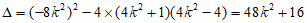 ,
,
所以当k为任何实数时,都有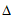 >0,
>0,
所以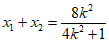 ,
,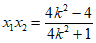 。
。
因为线段PQ的中点为M,
所以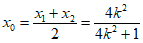 ,
,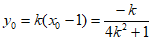 。
。
因为B(1,0)。
所以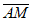 =
=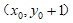 ,
,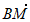 =
=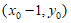 。
。
所以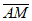 ·
·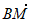 =
=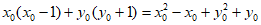
=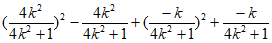
=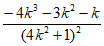
=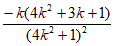
=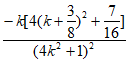
又因为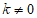 ,
,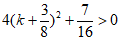 ,
,
所以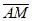 ·
·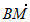 ≠0,
≠0,
所以点M不在以AB为直径的圆上。 14分
20. (本小题15分)
(I)解: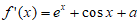 ,
,
对于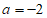 ,
,
当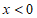 时,
时,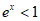 ,
,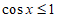 ,
,
所以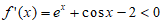 ,
,
所以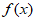 在
在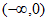 上单调递减。 4分
上单调递减。 4分
(II)解:当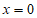 时,
时,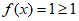 ,对于任意a
,对于任意a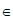 R,命题成立;
R,命题成立;
当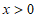 时,设
时,设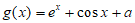 ,
,
则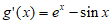 ,
,
因为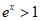 ,
,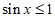 ,
,
所以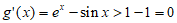 ,
,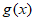 在
在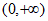 上单调递增,
上单调递增,
又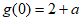 ,
,
所以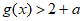 ,
,
所以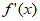 在
在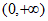 上单调递增,且
上单调递增,且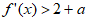 ,
,
①当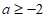 时,
时,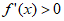 ,
,
所以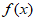 在
在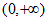 上单调递增。
上单调递增。
因为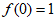 ,
,
所以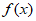 >1恒成立。
>1恒成立。
②当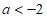 时,
时,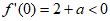 ,
,
因为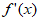 在
在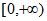 上单调递增,
上单调递增,
又当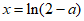 时,
时,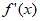 =
=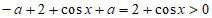 ,
,
所以存在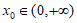 ,对于
,对于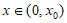 ,
,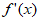 <0恒成立。
<0恒成立。
所以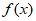 在
在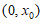 上单调递减,
上单调递减,
所以当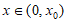 时,
时,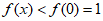 ,不合题意。
,不合题意。
综上,当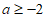 时,对于任意
时,对于任意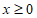 ,
,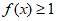 恒成立。 13分
恒成立。 13分
(III)解: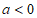 。 15分
。 15分
21. (本小题14分)
(I)解:X(A,B)=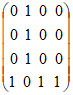 。 3分
。 3分
(II)证明:”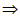 ”
”
若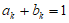 (k=1,2,…,n),由于
(k=1,2,…,n),由于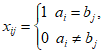
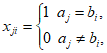
令A:a1,a2,…,an,由此数列B:1-a1,1-a2,…,1-an,
由于ai=bj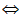 ai=1-aj
ai=1-aj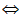 ai+ aj=1
ai+ aj=1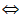 aj=1- ai
aj=1- ai
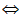 aj= bi。
aj= bi。
从而有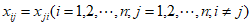 。
。
“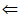 ”
”
若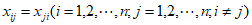 。
。
由于A,B是不同的数列,
(1)设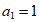 ,
,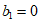 ,对任意的正整数
,对任意的正整数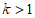 。
。
①若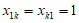 ,可得
,可得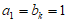 ,
,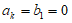 。
。
所以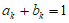 。
。
②若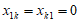 ,可得
,可得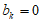 ,
,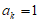 ,
,
所以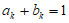 。
。
同理可证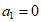 ,
,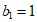 时,有
时,有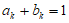 (k=1,2,…,n)成立。
(k=1,2,…,n)成立。
(2)设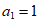 ,
,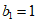 ,对任意的正整数
,对任意的正整数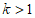 ,
,
①若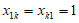 ,可得
,可得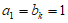 ,
,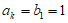 ,所以有
,所以有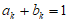 ,则A,B是相同的数列,不符合要求。
,则A,B是相同的数列,不符合要求。
②若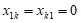 ,可得
,可得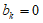 ,
,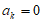 ,所以有
,所以有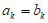 ,则A,B是相同的数列,不符合要求。
,则A,B是相同的数列,不符合要求。
同理可证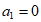 ,
,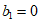 时, A,B是相同的数列,不符合要求。
时, A,B是相同的数列,不符合要求。
综上,有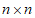 数表X(A,B)满足”
数表X(A,B)满足”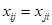 “的充分必要条件为”
“的充分必要条件为”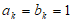 (k=1,2,…,n)”。
(k=1,2,…,n)”。
11分
(III)证明:由于数列A,B中的1共有n个,设A中1的个数为p,
由此有,A中0的个数为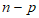 ,B中1的个数为
,B中1的个数为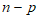 ,B中0的个数为p。
,B中0的个数为p。
若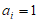 ,则数表X(A,B)的第i行为数列B:b1,b2,…,bn,
,则数表X(A,B)的第i行为数列B:b1,b2,…,bn,
若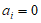 ,则数表X(A,B)的第i行为数列B:1-b1,1-b2,…,1-bn,
,则数表X(A,B)的第i行为数列B:1-b1,1-b2,…,1-bn,
所以数表X(A,B)中1的个数为p(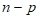 )+(
)+(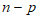 )p=2p(
)p=2p(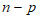 )≤2
)≤2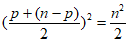 。
。
所以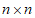 数表X(A,B)中1的个数不大于
数表X(A,B)中1的个数不大于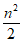 。 14分
。 14分
