本试卷共三道大题,28道小题,满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1—8题均有四个选项,符合题意的选项只有一个。
1. 2019年上半年北京市实现地区生产总值15212.5亿元,同比增长6.3%,总体来看,经济保持平稳运行,高质量发展,将数据15212.5用科学记数法表示应为
A. 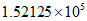 B.
B.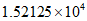
C. 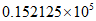 D.
D.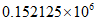
2. 如图是某几何体的三视图,该几何体是
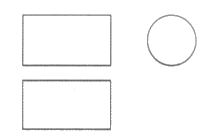
A. 长方体 B. 正方体 C. 球 D. 圆柱
3. 如图,将一块含有30°角的直角三角板的顶点放在直尺的一边上,若∠1=48°,则∠2的度数是
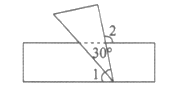
A. 48° B. 78° C. 92° D. 102°
4. 将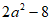 分解因式,结果正确的是
分解因式,结果正确的是
A. 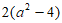 B.
B. 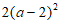 C.
C. 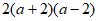 D.
D.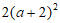
5. 点O,A,B,C在数轴上的位置如图所示,O为原点,AC=1,OA=OB,若点C所表示的数为a,则点B所表示的数为
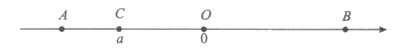
A. 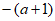 B.
B. 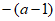 C.
C. 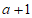 D.
D.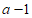
6. 已知锐角∠AOB,如图,
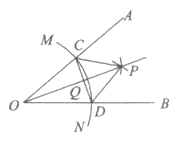
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作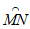 ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,两孤交于点P,连接CP,DP;
(3)作射线OP交CD于点Q。
根据以上作图过程及所作图形,下列结论中错误的是
A. CP∥OB B. CP=2QC
C. ∠AOP=∠BOP D. CD⊥OP
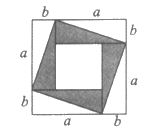
7. 将4张长为a、宽为b(a>b)的长方形纸片按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积之和为S1,阴影部分的面积之和为S2,若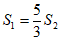 ,则
,则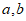 满足
满足
A. 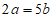 B.
B. 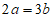 C.
C. 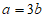 D.
D.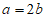
8. 党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础,以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分。
人数 地区 | 2017 | 2018 | 2019 |
东部 | 300 | 147 | 47 |
中部 | 1112 | 181 | |
西部 | 1634 | 916 | 323 |
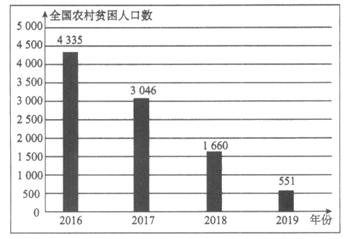
(以上数据来源于国家统计局)
根据统计图表提供的信息,下面推断不正确的是
A. 2018年中部地区农村贫困人口为597万人
B. 2017—2019年,农村贫困人口数量都是东部最少
C. 2016—2019年,农村贫困人口减少数量逐年增多
D. 2017—2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低
二、填空题(本题共16分,每小题2分)
9. 若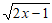 在实数范围内有意义,则实数x的取值范围是__________。
在实数范围内有意义,则实数x的取值范围是__________。
10. 随机从1,2,3,4中任取两个不同的数,分别记为a和b,则a+b>4的概率是__________。
11. 若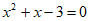 ,则代数式
,则代数式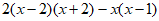 的值是___________。
的值是___________。
12. 如果一个正n边形的每个内角为108°,那么这个正n边形的边数为_________。
13. 《九章算术》中有这样一个题:”今有醇酒一斗,直钱五十;行酒一斗,直钱一十,今将钱三十,得酒二斗,问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱。现有30钱,买得2斗酒,问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为______________。
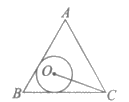
14. 如图,半径为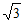 的⊙O与边长为8的等边三角形ABC的两边AB,BC都相切,连接OC,则tan∠OCB=____________。
的⊙O与边长为8的等边三角形ABC的两边AB,BC都相切,连接OC,则tan∠OCB=____________。
15. 甲、乙两队参加了”端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,根据图象有以下四个判断:
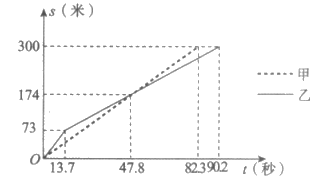
①乙队率先到达终点;
②甲队比乙队多走了126米;
③在47.8秒时,两队所走路程相等;
④从出发到13.7秒的时间段内,甲队的速度比乙队的慢。
所有正确判断的序号是_______________。
16. 从-1,0,2,3四个数中任取两个不同的数(记作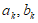 )构成一个数对
)构成一个数对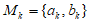 (其中
(其中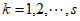 ,且将
,且将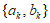 与
与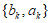 视为同一个数对),若满足:对于任意的
视为同一个数对),若满足:对于任意的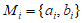 和
和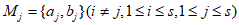 都有
都有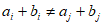 ,则s的最大值是__________。
,则s的最大值是__________。
三、解答题(本题共68分,第17—22题。每小题5分,第23—26题,每小题6分,第27—28题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 计算: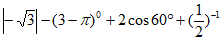 。
。
18. 解不等式组: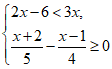
19. 观察下列分式方程的求解过程,指出其中错误的步骤,说明错误的原因,并直接给出正确结果。
解分式方程: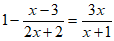 。
。
解:去分母,得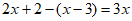 , 步骤1
, 步骤1
去括号,得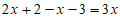 , 步骤2
, 步骤2
移项,得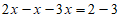 , 步骤3
, 步骤3
合并同类项,得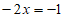 , 步骤4
, 步骤4
解得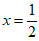 , 步骤5
, 步骤5
所以,原分式方程的解为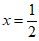 。 步骤6
。 步骤6
20. 已知关于x的方程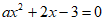 有两个不相等的实数根。
有两个不相等的实数根。
(1)求a的取值范围;
(2)若此方程的一个实数根为1,求a的值及方程的另一个实数根。
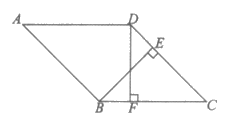
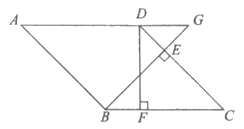
21. 如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F。
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,求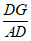 的值。
的值。
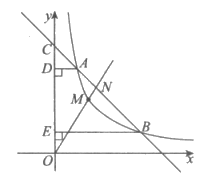
22. 如图,一次函数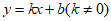 的图象与反比例函数
的图象与反比例函数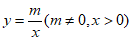 的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E,已知
的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E,已知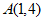 ,
,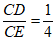 。
。
(1)求m的值和一次函数的解析式;
(2)若点M为反比例函数图象在A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标。
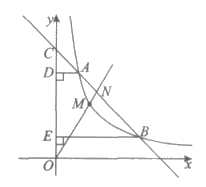
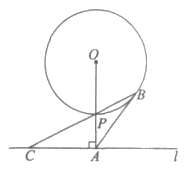
23. 如图,直线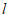 与⊙O相离,OA⊥
与⊙O相离,OA⊥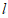 于点A,与⊙O相交于点P,
于点A,与⊙O相交于点P,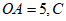 是直线
是直线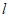 上一点,连接CP并延长,交⊙O于点B,且
上一点,连接CP并延长,交⊙O于点B,且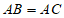 。
。
(1)求证:AB是⊙O的切线;
(2)若tan∠ACB=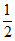 ,求线段BP的长。
,求线段BP的长。
24. 人口数据又称为人口统计数据,是指国家和地区的相关人口管理部门通过户口登记、人口普查等方式统计得出的相关数据汇总,人口数据对国家和地区的人口状况、管理以及各项方针政策的制定都具有重要的意义,下面是关于人口数据的部分信息。
a. 2018年中国大陆(不合港澳台)31个地区人口数量(单位:千万人)的频数分布直方图(数据分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x≤12):
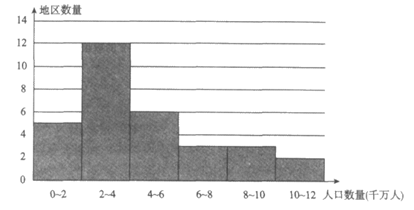
b. 人口数量在2≤x<4这一组的是:
2.2 2.4 2.5 2.5 2.6 2.7 3.1 3.6 3.7 3.8 3.9 3.9
c. 2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)、出生率(单位:‰)、死亡率(单位:‰)的散点图:
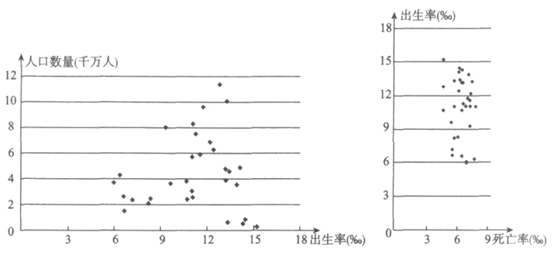
d. 下表是我国三次人口普查中年龄结构构成情况:
0~14岁人口比例 | 15~59岁人口比例 | 60岁及以上人口比例 | |
第二次人口普查 | 40.4% | 54.1% | 5.5% |
第五次人口普查 | 22.89% | 66.78% | 10.33% |
第六次人口普查 | 16.6% | 70.14% | 13.26% |
e. 世界各国的人口出生率差别很大,出生率可分为五等,最高>50‰,最低<20‰,2018年我国人口出生率降低至10.94‰,比2017年下降1.43个千分点。
根据以上信息,回答下列问题:
(1)2018年北京人口为2.2千万人,我国大陆(不含港澳台)地区中,人口数量从低到高排列,北京排在第___________位。
(2)人口增长率=人口出生率-人口死亡率,我国大陆(不含港澳台)地区中人口在2018年出现负增长的地区有___________个,在这些地区中,人口数量最少的地区人数为____________千万人(保留小数点后一位)。
(3)下列说法中合理的是_________________。
①我国人口基数较大,即使是人口出生率和增长率都缓慢增长的前提下,人口总数仍然是在不断攀升的,所以我国计划生育的基本国策是不变的;
②随着我国老龄化越来越严重,所以出台了”二孩政策”,目的是为了缓解老龄化的压力。
25. 如图,P是线段AB上的一点,AB=6cm,O是AB外一定点。连接OP,将OP绕点O顺时针旋转120°得OQ,连接PQ,AQ。
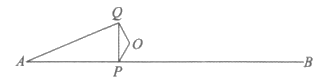
小明根据学习函数的经验,对线段AP,PQ,AQ的长度之间的关系进行了探究。
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,PQ,AQ的长度(单位:cm)的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP,PQ,AQ的长度这三个量中,确定___________的长度是自变量,____________的长度和__________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
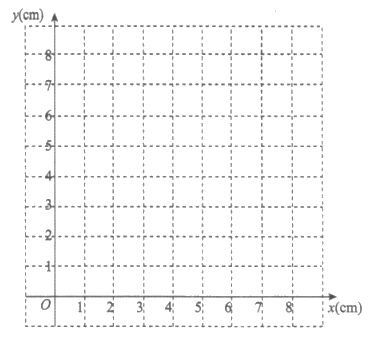
(3)结合函数图象,解决问题:当AQ=PQ时,线段AP的长度约为__________cm。
26. 在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点。直线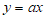 与抛物线
与抛物线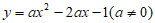 围成的封闭区域(不包含边界)为W。
围成的封闭区域(不包含边界)为W。
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当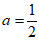 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围。
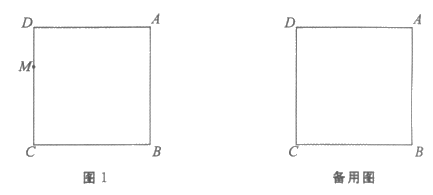
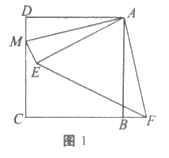
27. 如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF。
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值。
28. 在△ABC中,CD是△ABC的中线,如果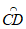 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称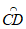 为△ABC的中线弧。
为△ABC的中线弧。
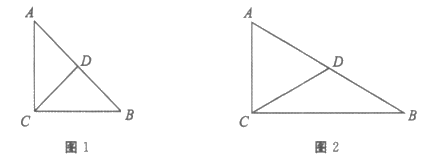
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点。
①如图1,若∠A=45°,画出△ABC的一条中线弧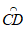 ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧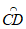 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如果2,若∠A=60°,求出△ABC的最长的中线弧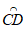 的弧长
的弧长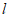 。
。
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点,求△ABC的中线弧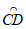 所在圆的圆心P的纵坐标t的取值范围。
所在圆的圆心P的纵坐标t的取值范围。
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | D | D | C | B | A | C | C |
二、填空题(本题共16分,每小题2分)
9. 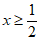 10.
10. 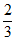 11. -5 12. 5
11. -5 12. 5
13. 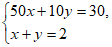 14.
14. 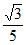 15. ③④ 16. 5
15. ③④ 16. 5
三、解答题(本题共68分,第17—22题,每小题5分,第23—26题,每小题6分,第27—28题,每小题7分)
17. 解:原式=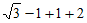 4分
4分
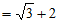 。 5分
。 5分
18. 解: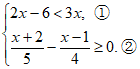
由①得,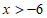 , 2分
, 2分
由②得,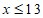 , 4分
, 4分
∴不等式组的解集为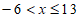 。 5分
。 5分
19. 解:错误的步骤是:步骤1、2、3、6,理由略, 4分
正确的结果是x=1。 5分
20. 解:(1)∵关于x的方程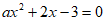 有两个不相等的实数根,
有两个不相等的实数根,
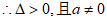 ,
,
即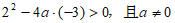 ,
,
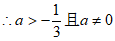 。 3分
。 3分
(2)将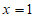 代入方程
代入方程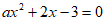 ,
,
解得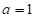 。
。
将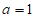 代入方程
代入方程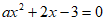 ,
,
解方程得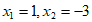 ,
,
∴方程的另一个根为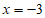 。 5分
。 5分
21. (1)证明:∵四边形ABCD为菱形,
∴CB=CD。
又∵BE⊥CD于点E,DF⊥BC于点F,
∴∠BEC=∠DFC=90°。
∵∠C=∠C,
∴△BEC≌△DFC,
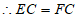 ,
,
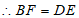 。 2分
。 2分
(2)解:设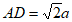 ,
,
∵∠A=45°,
∴△DEG和△BEC都是等腰直角三角形。
∵四边形ABCD为菱形,
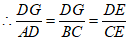 ,
,
可求出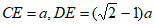 ,
,
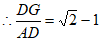 。 5分
。 5分
22. 解:(1)将点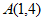 代入
代入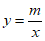 ,
,
得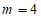 。
。
∴反比例函数解析式为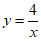 ,
,
∵BE⊥y轴,AD⊥y轴,
∴∠CEB=∠CDA=90°,
∴△CDA∽△CEB。
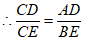 ,
,
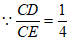 ,
,
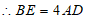 ,
,
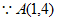 ,
,
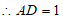 ,
,
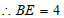 ,
,
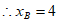 ,
,
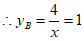 。
。
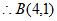 。
。
将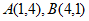 代入
代入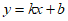 ,
,
得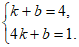
解得,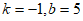 。
。
∴一次函数的解析式为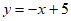 。 3分
。 3分
(2)当MN长度最大时,点M的坐标为(2,2)。 5分
23. (1)证明:如图,连接OB,则OP=OB。
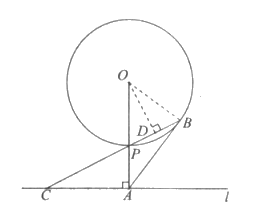
∴∠OBP=∠OPB=∠CPA,
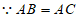
∴∠ACB=∠ABC,
而OA⊥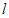 ,即∠OAC=90°,
,即∠OAC=90°,
∴∠ACB+∠CPA=90°,
即∠ABP+∠OBP=90°,
∴∠ABO=90°,
∴OB⊥AB,故AB是⊙O的切线。 2分
(2)解:∵tan∠ACB=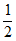 ,
,
∴在Rt△ACP中,设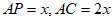 ,
,
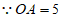 ,
,
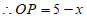 ,
,
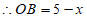 ,
,
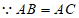 ,
,
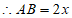 ,
,
∵∠ABO=90°,
由勾股定理,得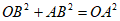 ,
,
即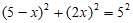 ,
,
解得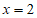 ,
,
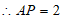 ,
,
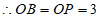 ,
,
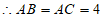 ,
,
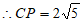 。
。
过O作OD⊥PB于D,
在△ODP和△CAP中,
∵∠OPD=∠CPA,∠ODP=∠CAP=90°,
∴△ODP∽△CAP,
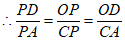 ,
,
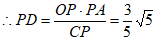 ,
,
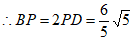 。 6分
。 6分
24. 解:(1)6; 2分
(2)2,3.8; 4分
(3)①②。 6分
25. 解:(1)AP,PQ,AQ; 3分
(2)如图所示:
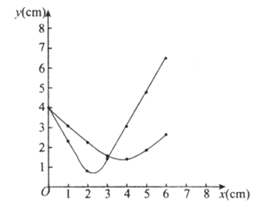
5分
(3)3.07。 6分
26. 解:(1)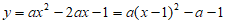 ,
,
∴抛物线顶点坐标为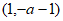 。 2分
。 2分
(2)当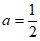 时,画出直线
时,画出直线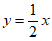 和抛物线
和抛物线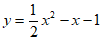 围成的封闭区域W,
围成的封闭区域W,
∴区域W内的所有整点坐标分别为(1,0),(2,0),(1,-1),(3,1)。 4分
(3)①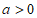 ,
,
当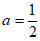 时,区域W内的所有整点有4个;
时,区域W内的所有整点有4个;
当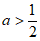 时,区域W内的所有整点多于3个;
时,区域W内的所有整点多于3个;
当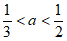 时,区域W内的所有整点有4个;
时,区域W内的所有整点有4个;
当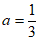 时,区域W内的所有整点有3个;
时,区域W内的所有整点有3个;
当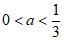 时,区域W内的所有整点多于3个。
时,区域W内的所有整点多于3个。
②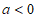 ,
,
当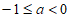 时,区域W内的所有整点有0个;
时,区域W内的所有整点有0个;
当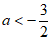 时,区域W内的所有整点多于3个。
时,区域W内的所有整点多于3个。
∴区域W内有3个整点时,a的取值范围是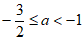 ,
,
综上,a的取值范围是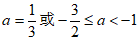 。 6分
。 6分
27. 解:(1)补全图形如图1所示。 1分
(2)如图2,连接BM。
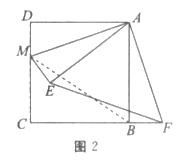
∵点D与点E关于AM所在的直线对称,
∴AE=AD,∠MAD=∠MAE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°。
又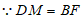 ,
,
∴△ADM≌△ABF,
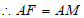 ,∠FAB=∠MAD,
,∠FAB=∠MAD,
∴∠FAB=∠MAE,
∴∠FAB+∠BAE=∠BAE+∠MAE,
∴∠FAE=∠MAB,
∴△FAE≌△MAB(SAS),
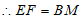 。
。
∵四边形ABCD是正方形,
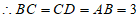 ,
,
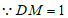 ,
,
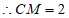 ,
,
∴在Rt△BCM中,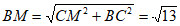 ,
,
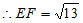 。 5分
。 5分
(3)当点M在CD边上运动时,若使△AEF为等腰三角形,则tan∠DAM=1或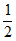 。
。
7分
28. 解:(1)①如图(答案不唯一)。
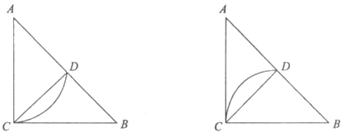
中线弧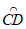 所在圆的半径r的最小值为
所在圆的半径r的最小值为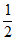 。 2分
。 2分
②当中线弧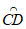 所在圆与AC,AB都相切时,中线弧
所在圆与AC,AB都相切时,中线弧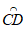 的弧长
的弧长 最大。
最大。
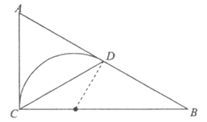
如图,此时中线弧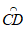 所在圆的圆心在BC上,半径为
所在圆的圆心在BC上,半径为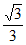 。
。
所以最大弧长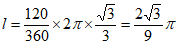 。 3分
。 3分
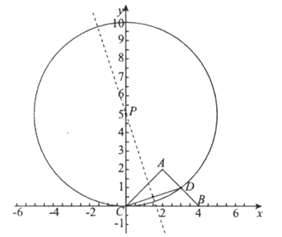
(2)△ABC的中线弧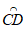 所在圆的圆心P在CD的垂直平分线上,
所在圆的圆心P在CD的垂直平分线上,
如图,若中线弧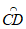 在CD下方,
在CD下方,
当中线弧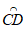 所在圆与BC相切时,可得圆心P的坐标为(0,5)。
所在圆与BC相切时,可得圆心P的坐标为(0,5)。
所以△ABC的中线弧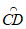 所在圆的圆心P的纵坐标
所在圆的圆心P的纵坐标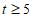 。
。
如图,若中线弧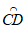 在CD上方,
在CD上方,
当中线弧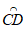 所在圆与AC相切时,可得圆心P的坐标为
所在圆与AC相切时,可得圆心P的坐标为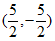 。
。
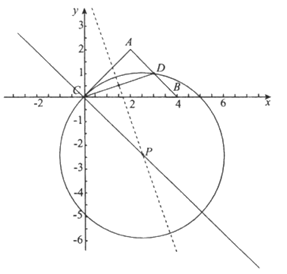
所以△ABC的中线弧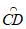 所在圆的圆心P的纵坐标
所在圆的圆心P的纵坐标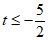 。
。
综上,△ABC的中线弧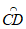 所在圆的圆心P的纵坐标t的取值范围为:
所在圆的圆心P的纵坐标t的取值范围为: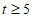 或
或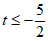 。
。
7分

 年份
年份