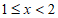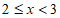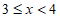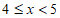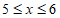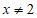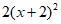本试卷共三道大题,28道小题,满分100分。考试时间120分钟。
一、选择题(本题共16分,每小题2分)
下面1—8题均有四个选项,其中符合题意的选项只有一个。
1. 自2020年1月23日起,我国仅用10天左右就完成了总建筑面积约为113 800平方米的雷神山医院和火神山医院的建设,彰显了”中国速度”,将113 800用科学记数法表示应为
A. 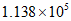 B.
B. 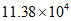 C.
C. 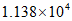 D.
D.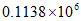
2. 下图是某几何体的三视图,该几何体是
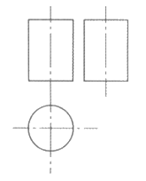
A. 圆锥 B. 球 C. 长方体 D. 圆柱
3. 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是
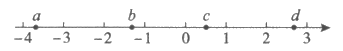
A. a B. b C. c D. d
4. 一个不透明的袋中装有8个黄球,m个红球,n个白球,每个球除颜色外都相同,任意摸出一个球,是黄球的概率与不是黄球的概率相同,下列m与n的关系一定正确的是
A. 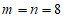 B.
B. 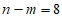 C.
C. 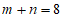 D.
D.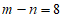
5. 如果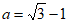 ,那么代数式
,那么代数式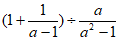 的值为
的值为
A. 3 B. 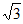 C.
C. 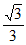 D.
D.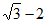
6. 如图,⊙O的直径AB垂直于弦CD,垂足为E,CD=4,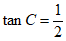 ,则AB的长为
,则AB的长为
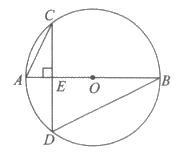
A. 2.5 B. 4 C. 5 D. 10
7. 如图,直线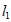 ∥
∥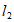 ,点A在直线
,点A在直线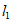 上,以点A为圆心,适当长度为半径画弧,分别交直线
上,以点A为圆心,适当长度为半径画弧,分别交直线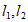 于B,C两点,以点C为圆心,CB长为半径画弧,与前弧交于点D(不与点B重合),连接
于B,C两点,以点C为圆心,CB长为半径画弧,与前弧交于点D(不与点B重合),连接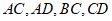 ,其中AD交
,其中AD交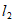 于点E,若∠ECA=40°,则下列结论错误的是
于点E,若∠ECA=40°,则下列结论错误的是
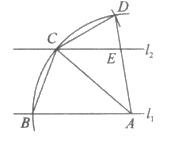
A. ∠ABC=70° B. ∠BAD=80° C. 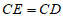 D.
D.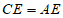
8. 生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段,为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的m天数据,整理后绘制成统计表进行分析。
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 | b | 3 | m | |
频率 | 0.05 | 0.10 | a | 0.15 | 1 |
表中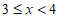 组的频率a满足
组的频率a满足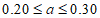 。
。
下面有四个推断:
①表中m的值为20;
②表中b的值可以为7;
③这m天的日均可回收物回收量的中位数在4≤x<5组;
④这m天的日均可回收物回收量的平均数不低于3。
所有合理推断的序号是
A. ①② B. ①③ C. ②③④ D. ①③④
二、填空题(本题共16分,每小题2分)
9. 若分式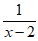 有意义,则x的取值范围是___________。
有意义,则x的取值范围是___________。
10. 分解因式: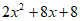 =___________。
=___________。
11. 如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,若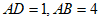 ,则
,则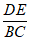 =__________。
=__________。
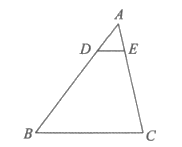
12. 如图所示的网格是正方形网格,则∠AOB_________∠COD(填”>”,”=”或”<”)。
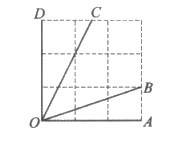
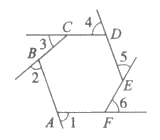
13. 如图,∠1~∠6是六边形ABCDEF的外角,则∠1+∠2+∠3+∠4+∠5+∠6=________°。
14. 用一个a的值说明命题”若a为实数,则a<2a”是错误的,这个值可以是a=____________。
15. 某地扶贫人员甲从办公室出发,骑车匀速前往A村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同路线匀速去追甲,乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往A村,甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(乙给甲手机的时间忽略不计)。有下列三个说法:
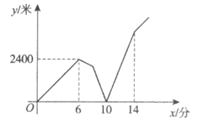
①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟。
其中所有正确说法的序号是__________。
16. 某兴趣小组外出登山,乘坐缆车费用如下表所示:
乘坐缆车方式 | 乘坐缆车费用(单位:元/人) |
往返 | 180 |
单程 | 100 |
已知小组成员每个人都至少乘坐一次缆车,去程时有8人乘坐缆车,返程时有17人乘坐缆车,他们乘坐缆车的总费用是2400元,该小组共有___________人。
三、解答题(本题共68分,第17—22题,每小题5分,第23—26题,每小题6分,第27,28题,每小题7分)
17. 计算: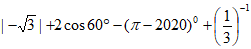 。
。
18. 解不等式组: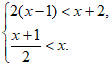
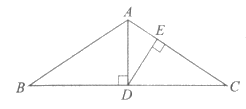
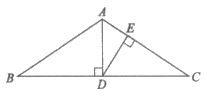
19. 如图,在△ABC中,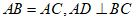 于点D,DE⊥AC于点E。
于点D,DE⊥AC于点E。
求证:∠BAD=∠CDE。
20. 关于x的一元二次方程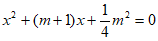 有两个不相等的实数根。
有两个不相等的实数根。
(1)求m的取值范围;
(2)写出一个符合条件的m的值,并求出此时方程的根。
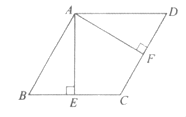
21. 如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF。
(1)求证:四边形ABCD是菱形;
(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE=2,求EG的长。
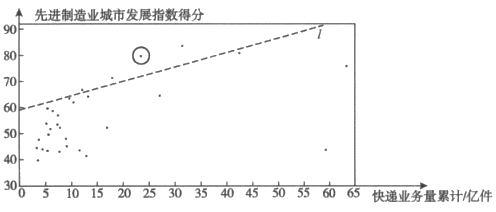
22. 先进制造业城市发展指数是反映一个城市先进制造水平的综合指数,对2019年我国先进制造业城市发展指数得分排名位居前列的30个城市的有关数据进行收集、整理、描述和分析。下面给出了部分信息:
a. 先进制造业城市发展指数得分的频数分布直方图(数据分成6组:
30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x≤90):
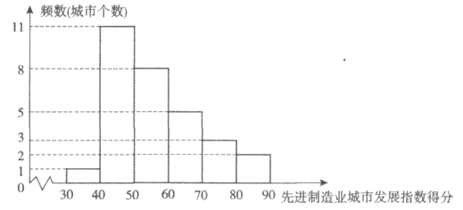
b. 先进制造业城市发展指数得分在70≤x<80这一组的是:71.1 75.7 79.9
c. 30个城市的2019年快递业务量累计和先进制造业城市发展指数得分情况统计图:
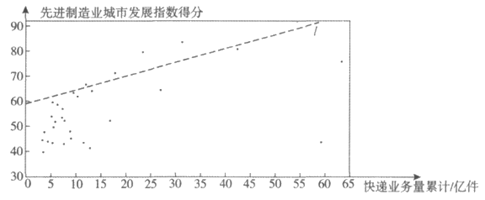
d. 北京的先进制造业城市发展指数得分为79.9。
根据以上信息,回答下列问题:
(1)在这30个城市中,北京的先进制造业城市发展指数得分排名第__________;
(2)在30个城市的快递业务量累计和先进制造业城市发展指数得分情况统计图中,包括北京在内的少数几个城市所对应的点位于虚线l的上方,请在图中用”○”圈出代表北京的点;
(3)在这30个城市中,先进制造业城市发展指数得分高于北京的城市的快递业务量累计的最小值约为_________亿件。(结果保留整数)
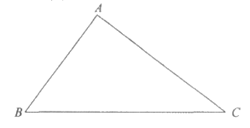
23. 如图,在△ABC中,AB=3,AC=4,BC=5,在同一平面内,△ABC内部一点O到AB,AC,BC的距离都等于a(a为常数),到点O的距离等于a的所有点组成图形G。
(1)直接写出a的值;
(2)连接BO并延长,交AC于点M,过点M作MN⊥BC于点N。
①求证:∠BMA=∠BMN;
②求直线MN与图形G的公共点个数。
24. 有这样一个问题:探究函数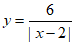 的图象与性质并解决问题。
的图象与性质并解决问题。
小明根据学习函数的经验,对问题进行了探究。
下面是小明的探究过程,请补充完整:
(1)函数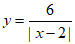 的自变量x的取值范围是
的自变量x的取值范围是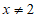 ;
;
(2)取几组y与x的对应值,填写在下表中,
x | … | -4 | -2 | -1 | 0 | 1 | 1.2 | 1.25 | 2.75 | 2.8 | 3 | 4 | 5 | 6 | 8 | … |
y | … | 1 | 1.5 | 2 | 3 | 6 | 7.5 | 8 | 8 | 7.5 | 6 | 3 | m | 1.5 | 1 | … |
m的值为___________;
(3)如下图,在平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点,并画出该函数的图象;
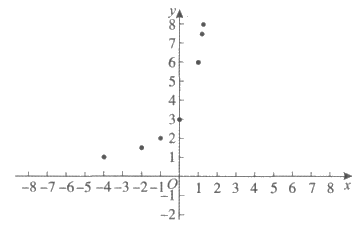
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数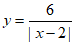 的图象是轴对称图形,它的对称轴是_________;
的图象是轴对称图形,它的对称轴是_________;
②过点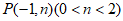 作直线
作直线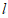 ∥x轴,与函数
∥x轴,与函数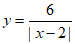 的图象交于点M,N(点M在点N的左侧),则
的图象交于点M,N(点M在点N的左侧),则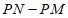 的值为____________。
的值为____________。
25. 在平面直角坐标系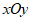 中,直线
中,直线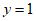 与一次函数
与一次函数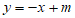 的图象交于点P,与反比例函数
的图象交于点P,与反比例函数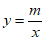 的图象交于点Q,点
的图象交于点Q,点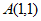 与点B关于y轴对称。
与点B关于y轴对称。
(1)直接写出点B的坐标;
(2)求点P,Q的坐标(用含m的式子表示);
(3)若P,Q两点中只有一个点在线段AB上,直接写出m的取值范围。
26. 在平面直角坐标系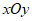 中,抛物线
中,抛物线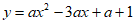 与y轴交于点A。
与y轴交于点A。
(1)求点A的坐标(用含a的式子表示);
(2)求抛物线的对称轴;
(3)已知点M(-2,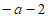 ),N(0,a),若抛物线与线段MN恰有一个公共点,结合函数图象,求a的取值范围。
),N(0,a),若抛物线与线段MN恰有一个公共点,结合函数图象,求a的取值范围。
27. 四边形ABCD是正方形,将线段CD绕点C逆时针旋转2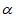 (0°<
(0°<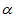 <45°),得到线段CE,连接DE,过点B作BF⊥DE交DE的延长线于点F,连接BE。
<45°),得到线段CE,连接DE,过点B作BF⊥DE交DE的延长线于点F,连接BE。
(1)依题意补全图1;
(2)直接写出∠FBE的度数;
(3)连接AF,用等式表示线段AF与DE的数量关系,并证明。

28. 在平面直角坐标系xOy中,点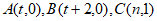 ,若射线OC上存在点P,使得△ABP是以AB为腰的等腰三角形,就称点P为线段AB关于射线OC的等腰点。
,若射线OC上存在点P,使得△ABP是以AB为腰的等腰三角形,就称点P为线段AB关于射线OC的等腰点。
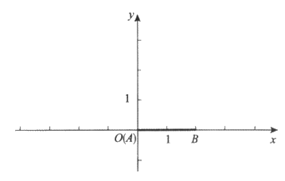
(1)如图,t=0,
①若n=0,则线段AB关于射线OC的等腰点的坐标是__________;
②若n<0,且线段AB关于射线OC的等腰点的纵坐标小于1,求n的取值范围;
(2)若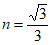 ,且射线OC上只存在一个线段AB关于射线OC的等腰点,则t的取值范围是______________。
,且射线OC上只存在一个线段AB关于射线OC的等腰点,则t的取值范围是______________。
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | D | A | C | B | C | C | D |
二、填空题(本题共16分,每小题2分)
题号 | 9 | 10 | 11 | 12 |
答案 |
|
|
| < |
题号 | 13 | 14 | 15 | 16 |
答案 | 360 | 答案不唯一,如 | ①②③ | 20 |
三、解答题(本题共68分,第17—22题,每小题5分,第23—26题,每小题6分,第27,28题,每小题7分)
17. 解:原式=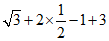 4分
4分
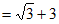 。 5分
。 5分
18. 解:原不等式组为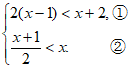
解不等式①得,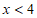 , 2分
, 2分
解不等式②得,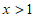 。 4分
。 4分
∴原不等式组的解集为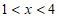 。 5分
。 5分
19. 证明: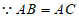 ,
,
∴∠B=∠C, 2分
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD+∠B=90°。 3分
∵DE⊥AC,
∴∠DEC=90°,
∴∠CDE+∠C=90°, 4分
∴∠BAD=∠CDE。 5分
20. 解:(1)由题意得,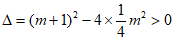 , 2分
, 2分
解得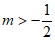 。 3分
。 3分
(2)答案不唯一,如: , 4分
, 4分
此时,方程为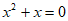 ,
,
解得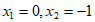 。 5分
。 5分
21. (1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC, 1分
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°。 2分
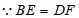 ,
,
∴△ABE≌△ADF,
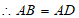 ,
,
∴四边形ABCD是菱形。 3分
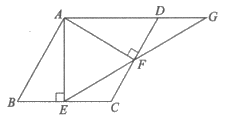
(2)解:由(1)知AD∥BC,
∴∠EAG=90°,∠G=∠CEG=30°, 4分
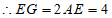 。 5分
。 5分
22. 答:(1)3; 2分
(2)
4分
(3)31。 5分
23. 解:(1)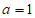 ; 1分
; 1分
(2)①由题意可知图形G是以O为圆心,a为半径的圆,AB,AC,BC与⊙O相切。
2分
∴∠ABM=∠NBM。
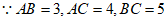 ,
,
∴∠A=90°。 3分
∵MN⊥BC,
∴∠A=∠BNM=90°,
∴∠BMA=∠BMN。 4分
②如图,设⊙O与AC的切点为D,连接OD,作OE⊥MN于点E。
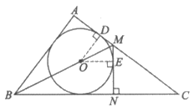
∴OD⊥AC, 5分
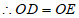 ,
,
∴OE为⊙O的半径,
∴MN为⊙O的切线,
∴直线MN与图形G的公共点个数为1。 6分
24. 解:(2)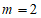 ; 1分
; 1分
(3)
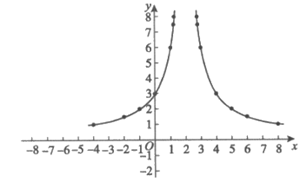 4分
4分
(4)①直线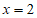 ; 5分
; 5分
②6。 6分
25. 解:(1)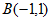 ; 2分
; 2分
(2)把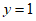 代入
代入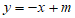 ,得
,得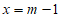 ,
,
把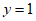 代入
代入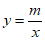 ,得
,得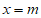 ,
,
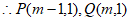 。 4分
。 4分
(3)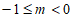 或
或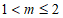 。 6分
。 6分
26. 解:
(1)∵抛物线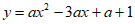 与y轴交于点A,
与y轴交于点A,
令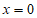 ,得
,得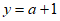 ,
,
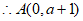 。 1分
。 1分
(2)由抛物线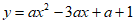 可知
可知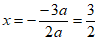 ,
,
∴抛物线的对称轴为直线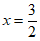 。 3分
。 3分
(3)对于任意的实数a,都有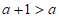 ,
,
可知点A总在点N的上方,
令抛物线上的点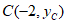 ,
,
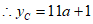 。
。
①如图1,当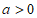 时,
时,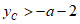 ,
,
∴点C在点M的上方,
结合函数图象,可知抛物线与线段MN没有公共点。
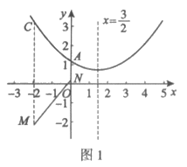
②当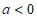 时,
时,
(i)如图2,当抛物线经过点M时,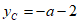 ,
,
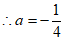 。
。
结合函数图象,可知抛物线与线段MN恰有一个公共点M。
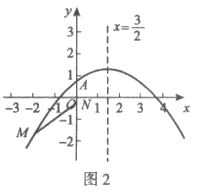
(ii)当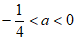 时,可知抛物线与线段MN没有公共点。
时,可知抛物线与线段MN没有公共点。
(iii)如图3,当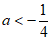 时,
时,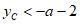 ,
,
∴点C在点M的下方。
结合函数图象,可知抛物线与线段MN恰有一个公共点。
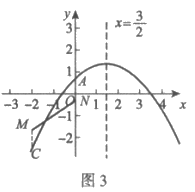
综上所述,a的取值范围是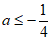 。 6分
。 6分
27. 解:(1)补全图形,如图所示。
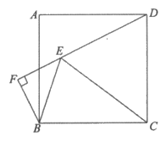
1分
(2)∠FBE=45°; 3分
(3)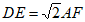 。 4分
。 4分
证明:如图,作AH⊥AF,交BF的延长线于点H,设DF与AB交于点G,根据题意可知,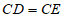 ,∠ECD=
,∠ECD=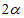 ,∠ABC=∠BCD=∠CDA=∠DAB=90°,
,∠ABC=∠BCD=∠CDA=∠DAB=90°,

∴∠EDC=90°-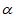 ,CB=CE,∠BCE=90°-
,CB=CE,∠BCE=90°-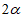 ,
,
∴∠CBE=45°+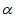 ,∠ADF=
,∠ADF=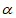 ,
,
∴∠ABE=45°-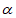 ,
,
∵BF⊥DE,
∴∠BFD=90°,
∵∠AGD=∠FGB,
∴∠FBG=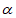 。
。
∴∠FBE=∠FEB=45°,
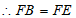 。 5分
。 5分
∵AH⊥AF,∠BAD=90°,
∴∠HAB=∠FAD,
∴△HAB≌△FAD, 6分
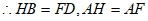 ,
,
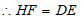 ,∠H=45°,
,∠H=45°,
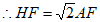 , 7分
, 7分
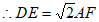 。
。
28. 解:(1)(0,2); 2分
(2)如图,设以点O为圆心,AB为半径的圆与直线y=1在第二象限的交点为D,作DE垂直x轴于点E,
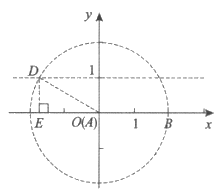
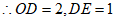 。
。
在Rt△ODE中,根据勾股定理得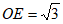 ,
,
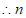 的取值范围是
的取值范围是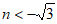 。 4分
。 4分
(3)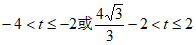 或
或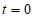 或
或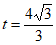 。 7分
。 7分