本试卷有三道大题,考试时长120分钟,满分150分
一、选择题:本大题共10小题,共40分。在各小题列出的四个选项中,有且只有一项是正确的,请选出符合要求的选项。
1. 若集合A={x|-2<x<1},B={x|x2-3x>0},则A B=( )
B=( )
A. {x|x<1或x>3} B. {x|-2<x<1}
C. {x|-2<x<0或x>3} D. {x|-2<x<0}
2. 下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A. 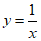 B.
B.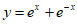
C. 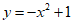 D.
D.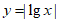
3. 直线Ax+By+1=0在y轴上的截距为1,且与直线3x+y+1=0垂直,则A等于( )
A. 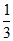 B. –
B. –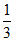 C. 3 D. -3
C. 3 D. -3
4. 设函数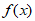 =
=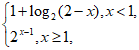 ,则
,则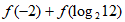 =( )
=( )
A. 12 B. 9 C. 6 D. 3
5. 已知m∈(0,1),令a=logm2,b=m2,c=2m,那么a,b,c之间的大小关系为( )
A. b<c<a B. b<a<c C. c<a<b D. a<b<c
6. 已知半径为1的圆经过点(4,3),则其圆心到原点的距离的最大值为( )
A. 4 B. 5 C. 6 D. 7
7. m=-1是直线mx+y-3=0与直线m(m-1)x-2y+2=0平行的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
8. 已知方程x·|x-a|=-1的解不少于两个,则实数a的取值范围是( )
A. a≤-2 B. a<-2 C. -2≤a<0 D. a>-2
9. 过点P(cos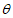 ,sin
,sin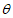 )作直线与圆C:x2+y2=4相交于A,B两点,则|AB|的取值范围是( )
)作直线与圆C:x2+y2=4相交于A,B两点,则|AB|的取值范围是( )
A. (0,2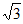 ] B. [2
] B. [2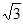 ,4] C. (0,4] D. [
,4] C. (0,4] D. [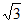 ,4]
,4]
10. 已知函数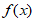 = asinx-2
= asinx-2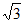 cosx的一条对称轴为x=-
cosx的一条对称轴为x=-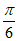 ,
,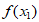 +
+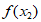 =0,且函数
=0,且函数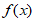 在(x1,x2)上具有单调性,则|x1+x2|的最小值为( )
在(x1,x2)上具有单调性,则|x1+x2|的最小值为( )
A. 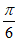 B.
B. 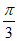 C.
C. 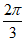 D.
D.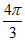
二、填空题:本大题共5小题,共25分。
11. 以抛物线y2=4x的焦点为圆心,并且与该抛物线的准线相切的圆的标准方程为_______。
12. 设双曲线C的一个焦点为(0,4),实轴长为4,则C的离心率为_______,C的渐近线方程为_______。
13. 若对任意x>0,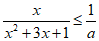 恒成立,则写出一个满足条件的a的取值为_________。
恒成立,则写出一个满足条件的a的取值为_________。
14. 已知函数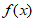 =
=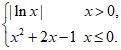 若
若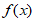 的图象与直线y=x-1的公共点的个数为_______。
的图象与直线y=x-1的公共点的个数为_______。
15. 已知曲线C的方程是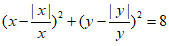 ,给出下列三个结论:
,给出下列三个结论:
①曲线C既是中心对称图形,又是轴对称图形;
②若点P,Q在曲线C上,则|PQ|的最大值是6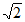 ;
;
③曲线C是一个封闭图形。
其中,所有正确结论的序号是_____________。
三、解答题:共6个小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16.(本小题满分14分)
已知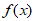 =sin2x+
=sin2x+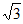 sinx sin
sinx sin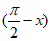 。
。
(I)求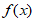 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(II)求函数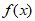 在区间
在区间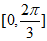 上的取值范围。
上的取值范围。
17.(本小题满分14分)
在△ABC中,A、B、C的对边分别是a、b、c,且满足(2b-c)cosA=acosC。
(I)求角A的大小;
(II)若a=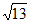 ,b+c=5,求△ABC的面积。
,b+c=5,求△ABC的面积。
18.(本小题满分14分)
已知函数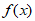 =a(x-1)-lnx,a>0。
=a(x-1)-lnx,a>0。
(I)当a=1时,求证:对任意x∈[1,+∞),有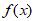 ≤
≤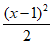 ;
;
(Ⅱ)求函数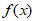 在区间[1,+∞)上的最小值。
在区间[1,+∞)上的最小值。
19.(本小题满分14分)
已知函数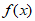 =
=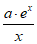 (a∈R,a≠0)。
(a∈R,a≠0)。
(I)当a=1时,求曲线y=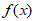 在点(1,
在点(1,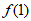 )处切线的方程;
)处切线的方程;
(Ⅱ)当a<0时,求函数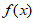 的单调区间;
的单调区间;
(III)当x∈(0,+∞)时,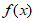 ≥1恒成立,求a的取值范围。
≥1恒成立,求a的取值范围。
20.(本小题满分14分)
已知椭圆C: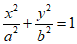 (a>b>0)的离心率为
(a>b>0)的离心率为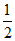 ,右焦点为F(c,0),左顶点为A,右顶点B在直线l:x=2上。
,右焦点为F(c,0),左顶点为A,右顶点B在直线l:x=2上。
(I)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线AP交直线l于点D,当点P运动时,判断以BD为直径的圆与直线PF的位置关系,并加以证明。
21.(本小题满分15分)
已知数列{xn},若对任意n∈N*,都有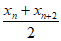 >xn+1成立,则称数列{xn}为”差增数列”。
>xn+1成立,则称数列{xn}为”差增数列”。
(I)试判断数列an=n2(n∈N*)是否为”差增数列”,并说明理由;
(Ⅱ)若数列{an}为”差增数列”,且an∈N*,a1=a2=1,对于给定的正整数m,当ak=m,项数k的最大值为20时,求m的所有可能取值的集合;
(III)若数列{lgxn}为”差增数列”,(n∈N*,n≤2020),且lgx1+lgx2+…+lgx2020=0,证明:x1010x1011<1。
参考答案
一、选择题,本大题共10小题,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | C | A | B | D | C | A | A | B | C |
二、填空题,本大题共5小题,共25分。
11.(x-1)2+y2=4;12. 2,y=±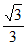 x;13. [0,5]中任取一个;14. 3;15. ①②
x;13. [0,5]中任取一个;14. 3;15. ①②
(注:12题前空3分,后空2分,15题错选和多选得0分,少选给3分,全对5分)
三、解答题,共6个小题,共85分。
16. 解:(I)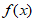 =sin2x+
=sin2x+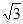 sins cosx=
sins cosx=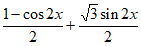
=sin(2x-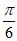 )+
)+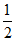 5分
5分
函数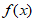 的最小正周期T=π 6分
的最小正周期T=π 6分
由2k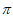 +
+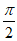 ≤2x-
≤2x-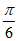 ≤2k
≤2k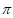 +
+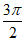 ,k∈Z,得k
,k∈Z,得k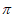 +
+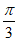 ≤x≤k
≤x≤k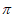 +
+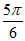 ,k∈Z,
,k∈Z,
故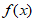 的单调减区间为[k
的单调减区间为[k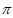 +
+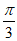 ,k
,k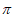 +
+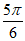 ],k∈Z 9分
],k∈Z 9分
(Ⅱ)由(I)得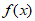 =sin
=sin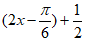 。
。
因为0≤x≤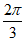 ,所以-
,所以-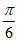 ≤2x-
≤2x-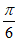 ≤
≤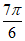 , 10分
, 10分
所以-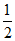 ≤sin
≤sin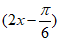 ≤1,当…… 13分
≤1,当…… 13分
因此0≤sin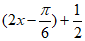 ≤
≤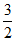 ,即
,即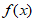 的取值范围为
的取值范围为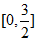 14分
14分
17. 解:(1)在△ABC中,由正弦定理得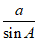 =
=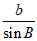 =
=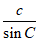 =2R
=2R
∴a=2R sinA,b=2R sinB,c=2RsinC
∴(2sinB-sinC)cosA=sin AcosC
∴2sinB cosA=sinC cosA+sinA cosC=sin(A+C)
∵A+B+C=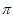 ,∴sin(A+C)=sinB
,∴sin(A+C)=sinB
∴2sinB cosA=sinB,∵B∈(0,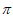 ),∴sinB≠0
),∴sinB≠0
∴cosA=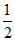 ,∵A∈(0,
,∵A∈(0,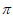 ),∴A=
),∴A=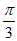 7分
7分
(2)在△ABC中,由余弦定理得a2=b2+c2-2bc cosA
∵a=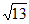 ,b+c=5 ∴13=(b+c)2-2bc-2bc cos
,b+c=5 ∴13=(b+c)2-2bc-2bc cos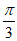 =25-3bc
=25-3bc
∴bc=4 ∴S△ABC=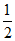 bc sinA=
bc sinA=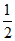 ×4×sin
×4×sin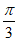 =
=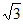 14分
14分
18. 解:(I)当a=1,x∈[1,+∞)时,设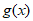 =
=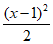 -(x-1)+lnx,a∈R。
-(x-1)+lnx,a∈R。
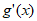 =(x-1)-1+
=(x-1)-1+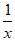 =
=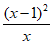 ≥0,所以
≥0,所以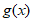 在[1,+∞)上为增函数,故
在[1,+∞)上为增函数,故
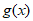 ≥
≥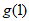 =0。 6分
=0。 6分
(Ⅱ)由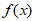 =a(x-1)-lnx可得
=a(x-1)-lnx可得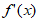 =a-
=a-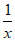 =
=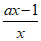 7分
7分
①当0<a<1时,令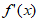 =a–
=a–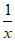 >0,得x>
>0,得x>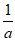 ;令
;令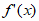 <0,得1≤x<
<0,得1≤x<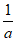 ,
,
所以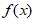 在[1,
在[1,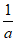 )上为减函数,
)上为减函数,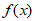 在(
在(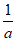 ,+∞)上为增函数。
,+∞)上为增函数。
故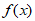 在[1,+∞)上的最小值为f(
在[1,+∞)上的最小值为f(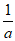 )=1-a+lna。 11分
)=1-a+lna。 11分
②当a≥1时,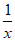 ≤1,故
≤1,故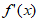 =a-
=a-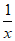 ≥0,
≥0,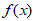 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,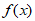 在x[1,+∞)上的最小值为
在x[1,+∞)上的最小值为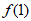 =0。 13分
=0。 13分
综上,当0<a<1时,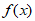 在[1,+∞)上的最小值为f(
在[1,+∞)上的最小值为f(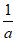 )=1-a+lna。
)=1-a+lna。
当a≥1时,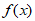 在[1,+∞)上的最小值为f(1)=0。 14分
在[1,+∞)上的最小值为f(1)=0。 14分
19. 解:(I)当a=1时,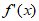 =
=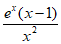 。依题意
。依题意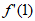 =0,
=0,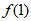 =e。
=e。
曲线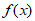 在x=1处切线的方程为y=e。 4分
在x=1处切线的方程为y=e。 4分
(Ⅱ)函数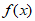 的定义域为{x|x≠0}。
的定义域为{x|x≠0}。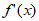 =
=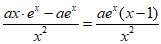 。
。
当a<0,当即x<0和0<x<1时,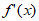 >0,当x>1时
>0,当x>1时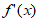 <0,
<0,
函数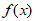 的单调增区间为(-∞,0),(0,1);单调减区间为(1,+∞)。 9分
的单调增区间为(-∞,0),(0,1);单调减区间为(1,+∞)。 9分
(III)当x∈(0,+∞)时,要使 =
=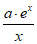 ≥1恒成立,即使a≥
≥1恒成立,即使a≥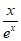 在x∈(0,+∞)时恒成立。设
在x∈(0,+∞)时恒成立。设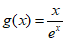 ,则
,则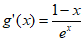 。可知在0<x<1时,
。可知在0<x<1时,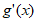 >0,
>0,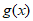 为增函数;
为增函数;
x>1时,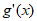 <0,
<0,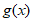 为减函数,则
为减函数,则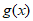 max=
max=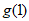 =
=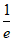 。
。
从而a≥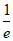 。 14分
。 14分
20. 解:(I)依题可知B(a,0),a=2,因为e=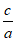 =
=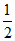 ,
,
所以c=1 b=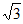 ,故椭圆C的方程为
,故椭圆C的方程为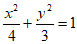 。 4分
。 4分
(Ⅱ)以BD为直径的圆与直线PF相切。
证明如下:由题意可设直线AP的方程为y=k(x+2)(k≠0)。
则点D坐标为(2,4k),BD中点E的坐标为(2,2k),
由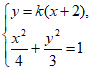 得(3+4k2)x2+16k2x+16k2-12=0。 8分
得(3+4k2)x2+16k2x+16k2-12=0。 8分
设点P的坐标为(x0,y0),则-2x0=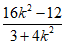 。
。
所以x0=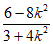 ,y0=k(x0+2)=
,y0=k(x0+2)=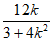 。
。
因为点F坐标为(1,0),
①当k=±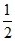 时,点P的坐标为(1,±
时,点P的坐标为(1,±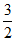 ),直线PF的方程为x=1,
),直线PF的方程为x=1,
点D的坐标为(2,±2)。
此时以BD为直径的圆(x-2)2+(y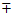 1)2=1与直线PF相切。 10分
1)2=1与直线PF相切。 10分
②当k≠±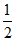 时,直线PF的斜率kPF=
时,直线PF的斜率kPF=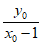 =
=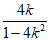 。
。
所以直线PF的方程为y=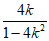 (x-1),即x-
(x-1),即x-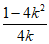 y-1=0。
y-1=0。
故点E到直线PF的距离
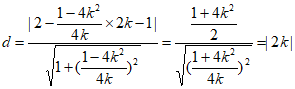
(或直线PF的方程为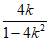 x-y-
x-y-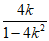 =0,
=0,
故点E到直线PF的距离
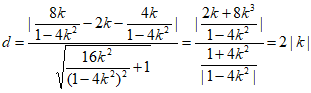 )
)
又因为|BD|=2R=4|k|,故以BD为直径的圆与直线PF相切。 13分
综上得,当点P运动时,以BD为直径的圆与直线PF相切。 14分
解法二:
(Ⅱ)以BD为直径的圆与直线PF相切。
证明如下:设点P(x0,y0),则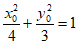 (y0≠0)
(y0≠0)
①当x0=1时,点P的坐标为(1,±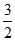 ),直线PF的方程为x=1,
),直线PF的方程为x=1,
点D的坐标为(2,±2),
此时以BD为直径的圆(x-2)2+(y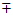 1)2=1与直线PF相切,
1)2=1与直线PF相切,
②当x0≠1时直线AP的方程为y=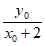 (x+2),
(x+2),
点D的坐标为D(2,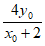 ),BD中点E的坐标为(2,
),BD中点E的坐标为(2,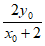 ),故|BE|=|
),故|BE|=|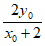 |
|
直线PF的斜率为kPF=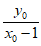 ,
,
故直线PF的方程为y=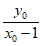 (x-1),即x-
(x-1),即x-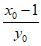 y-1=0,
y-1=0,
所以点E到直线PF的距离
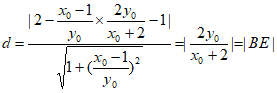
故以BD为直径的圆与直线PF相切。
综上可得,当点P运动时,以BD为直径的圆与直线PF相切。
21. 解:(1)数列an=n2(n∈N*)是”差增数列”。
因为任意的n∈N*,都有an+an+2=n2+(n+2)2=2n2+4n+4=2(n+1)2+2>2(n+1)2=2an+1,即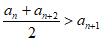 成立,
成立,
所以数列an=n2(n∈N*)是”差增数列”; 4分
(2)由已知,对任意的n∈N*,an+2-an+1>an+1-an恒成立。
可令bn=an+1-an(n≥1),则bn∈N,且bn<bn+1,
又an=m,要使项数k达到最大,且最大值为20时,必须bn(1≤n≤18)最小。
而b1=0,故b2=1,b3=2,…,bn=n-1。
所以an-a1=b1+b2+…+bn-1=0+1+2+…+(n-2)=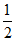 (n-1)(n-2),
(n-1)(n-2),
即当1≤n≤19时,an=1+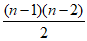 ,a19=154,因为k的最大值为20,
,a19=154,因为k的最大值为20,
所以18≤a20-a19<18+19,即18≤m-154<18+19,
所以m的所有可能取值的集合为{m|172≤m<191,m∈N*} 10分
(3)证明:(反证法)假设x1010x1011≥1。由已知可得xn(n=1,2,…,2020)均为正数,
且x1x2…x2020=1,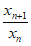 <
<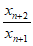 ,
,
而由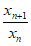 <
<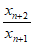 可得
可得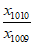 <
<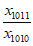 <
<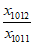 ,
,
即x1010x1011< x1009 x1012,所以x1009 x1012>1,
又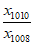 =
=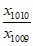 ·
·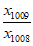 <
<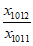 ·
·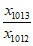 =
=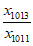 ,即x1008x1013>1,
,即x1008x1013>1,
同理可证x1007x1014>1,…,x1x2020>1,
因此x1x2…x2020>1,这与已知矛盾,
所以x1010x1011<1。 15分
