本试卷有三道大题,考试时长120分钟,满分150分。
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 若复数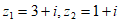 ,则
,则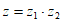 在复平面内的对应点位于( )
在复平面内的对应点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 圆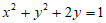 的半径为( )
的半径为( )
A. 1 B. 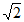 C. 2 D. 4
C. 2 D. 4
3. 已知向量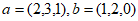 ,则
,则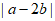 等于( )
等于( )
A. 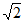 B.
B. 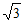 C. 2 D. 3
C. 2 D. 3
4. 若椭圆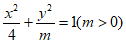 的离心率为
的离心率为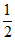 ,则实数m等于( )
,则实数m等于( )
A. 3 B. 1或3 C. 1或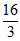 D. 3或
D. 3或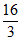
5. 关于直线a,b以及平面M,N,下列命题中正确的是( )
A. 若a∥M,b∥M,则a∥b B. 若a∥M,b⊥a,则b⊥M
C. 若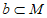 ,且a⊥b,则a⊥M D. 若a⊥M,a∥N,则M⊥N
,且a⊥b,则a⊥M D. 若a⊥M,a∥N,则M⊥N
6. “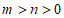 “是”方程
“是”方程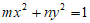 表示焦点在y轴上的椭圆”的( )
表示焦点在y轴上的椭圆”的( )
A. 充分但不必要条件 B. 必要但不充分条件
C. 充要条件 D. 既不充分又不必要条件
7. 在平面直角坐标系中,记d为点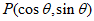 到直线
到直线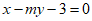 的距离,当
的距离,当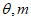 变化时,d的最大值为( )
变化时,d的最大值为( )
A. 1 B. 2 C. 3 D. 4
8. 已知矩形ABCD,AB=1,BC=x,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,则( )
A. 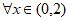 ,都存在某个位置,使得AB⊥CD
,都存在某个位置,使得AB⊥CD
B. 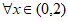 ,都不存在某个位置,使得AB⊥CD
,都不存在某个位置,使得AB⊥CD
C. 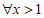 ,都存在某个位置,使得AB⊥CD
,都存在某个位置,使得AB⊥CD
D. 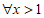 ,都不存在某个位置,使得AB⊥CD
,都不存在某个位置,使得AB⊥CD
9. 数学中有许多形状优美、寓意美好的曲线,曲线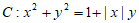 就是其中之一(如图)。给出下列三个结论:
就是其中之一(如图)。给出下列三个结论:
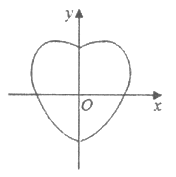
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过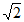 ;
;
③曲线C所围成的”心形”区域的面积小于3。
其中,所有正确结论的序号是( )
A. ① B. ② C. ①② D. ①②③
10. 已知正方体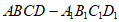 ,点
,点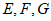 分别是线段
分别是线段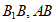 和
和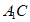 上的动点,观察直线CE与
上的动点,观察直线CE与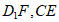 与
与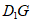 。给出下列结论:
。给出下列结论:
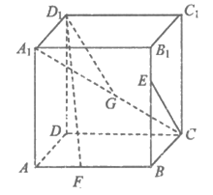
①对于任意给定的点E,存在点F,使得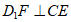 ;
;
②对于任意给定的点F,存在点E,使得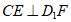 ;
;
③对于任意给定的点E,存在点G,使得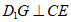 ;
;
④对于任意给定的点G,存在点E,使得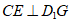 。
。
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题:共6小题,每小题5分,共30分。
11. 已知i为虚数单位,设复数z满足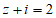 ,则
,则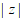 =__________。
=__________。
12. 在直角坐标系xOy中,在y轴上截距为-1且倾斜角为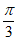 的直线方程为____________。
的直线方程为____________。
13. 若直线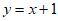 与椭圆
与椭圆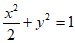 相交于A,B两个不同的点,则
相交于A,B两个不同的点,则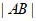 等于___________。
等于___________。
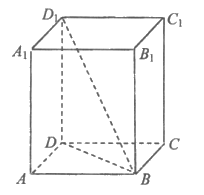
14. 如图,长方体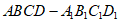 中,ABCD是边长为1的正方形,
中,ABCD是边长为1的正方形,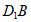 与平面ABCD所成的角为60°,则棱
与平面ABCD所成的角为60°,则棱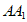 的长为____________;二面角
的长为____________;二面角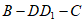 的大小为__________。
的大小为__________。
15. 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3。
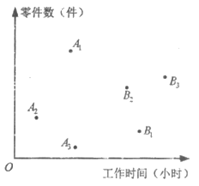
①记Qi为第i名工人在这一天中加工的零件总数,则Q1,Q2,Q3中最大的是____________;
②记pi为第i名工人在这一天中平均每小时加工的零件数,则p1,p2,p3中最大的是_____________。
16. 已知M为椭圆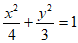 上一点,N为椭圆长轴上一点,O为坐标原点。
上一点,N为椭圆长轴上一点,O为坐标原点。
给出下列结论:
①存在点M,N,使得△OMN为等边三角形;
②不存在点M,N,使得△OMN为等边三角形;
③存在点M,N,使得∠OMN=90°;
④不存在点M,N,使得∠OMN=90°。
其中,所有正确结论的序号是___________。
三、解答题共6小题,共80分。解答应写出文字说明、演算步骤或证明过程。
17. 在平面直角坐标系xOy内有三个定点A(2,2),B(1,3),C(1,1),记△ABC的外接圆为E。
(Ⅰ)求圆E的方程;
(Ⅱ)若过原点O的直线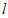 与圆E相交所得弦的长为
与圆E相交所得弦的长为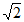 ,求直线
,求直线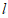 的方程。
的方程。
18. 在△ABC中,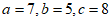 。
。
(Ⅰ)求sinA的值;
(Ⅱ)若点P为射线AB上的一个动点(与点A不重合),设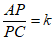 。
。
①求k的取值范围;
②直接写出一个k的值,满足:存在两个不同位置的点P,使得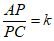 。
。
19. 如图,在长方体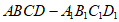 中,底面ABCD是正方形,
中,底面ABCD是正方形,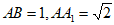 ,E是
,E是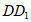 的中点。
的中点。
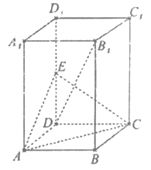
(Ⅰ)求证:AC⊥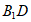 ;
;
(Ⅱ)求点B1到平面ACE的距离;
(Ⅲ)求二面角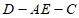 的大小。
的大小。
20. 已知椭圆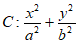 =1(
=1(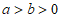 )的离心率为
)的离心率为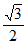 ,
,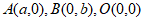 ,△OAB的面积为1。
,△OAB的面积为1。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N。
求证: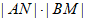 为定值。
为定值。
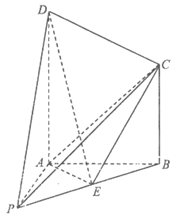
21. 如图,四棱锥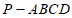 中,AD⊥平面ABP,BC∥AD,∠PAB=90°。
中,AD⊥平面ABP,BC∥AD,∠PAB=90°。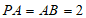 ,
,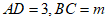 ,E是PB的中点。
,E是PB的中点。
(Ⅰ)证明:平面AEC⊥平面PBC;
(Ⅱ)若二面角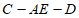 的余弦值是
的余弦值是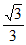 ,求m的值;
,求m的值;
(Ⅲ)若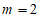 ,在线段AD上是否存在一点F,使得PF⊥CE。若存在,确定F点的位置;若不存在,说明理由。
,在线段AD上是否存在一点F,使得PF⊥CE。若存在,确定F点的位置;若不存在,说明理由。
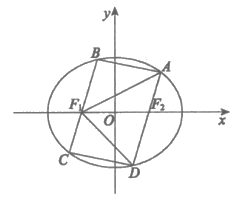
22. 如图,已知四边形ABCD是椭圆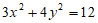 的内接平行四边形,且
的内接平行四边形,且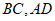 分别经过椭圆的焦点
分别经过椭圆的焦点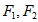 。
。
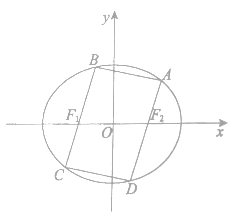
(Ⅰ)若直线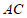 的方程为
的方程为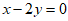 ,求AC的长;
,求AC的长;
(Ⅱ)求平行四边形ABCD面积的最大值。
【试题答案】
一、选择题:共10小题,每小题4分,共40分。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A | B | A | D | D | C | D | C | C | B |
二、填空题:共6小题,每小题5分,共30分。
11. 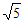 ; 12.
; 12. 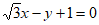 ; 13.
; 13. 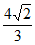 ; 14.
; 14. 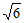 ,45°;
,45°;
15. 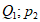 ; 16. ①④
; 16. ①④
三、解答题:共6小题,共80分。解答应写出文字说明、演算步骤或证明过程。
17. 解:(Ⅰ)设△ABC的外接圆E的圆心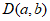 ,半径为
,半径为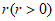 ,则E为:
,则E为: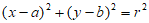 。
。
由题意,得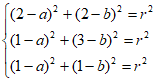 ,
,
解得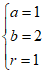 ,所以
,所以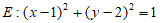 。
。
(Ⅱ)设直线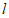 的方程为
的方程为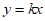 或
或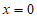 (舍)。
(舍)。
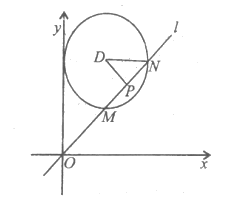
如图,设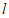 与圆E相交于点
与圆E相交于点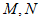 ,过圆心D作直线
,过圆心D作直线 的垂线,垂足为P,
的垂线,垂足为P,
所以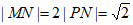 ,即
,即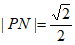 ,
,
在Rt△DPN中,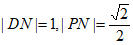 ,
,
所以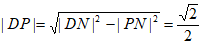 ,
,
又因为圆E的圆心到直线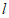 的距离
的距离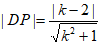 ,
,
所以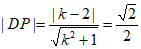 ,
,
解得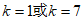 ,
,
故直线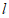 的方程为
的方程为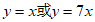 。
。
18. 解:(Ⅰ)在△ABC中,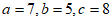 ,
,
根据余弦定理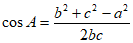
所以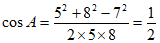 。
。
因为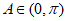 ,
,
所以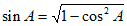
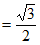 。
。
(Ⅱ)①在△ABC中,
根据正弦定理,得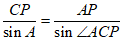 ,
,
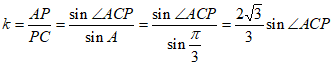
因为点P为射线AB上一动点,
所以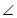
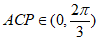 。
。
所以k的取值范围为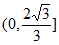 。
。
②答案不唯一,取值在区间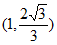 上均正确。
上均正确。
19. 因为 是长方体,底面ABCD是正方形,所以DA、DC、
是长方体,底面ABCD是正方形,所以DA、DC、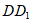 两两垂直,如图,以D为原点,直线
两两垂直,如图,以D为原点,直线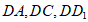 分别为x轴,y轴,z轴,建立空间直角坐标系。
分别为x轴,y轴,z轴,建立空间直角坐标系。
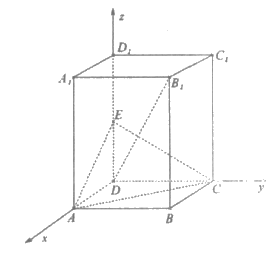
则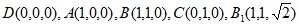 。
。
(Ⅰ)证明:因为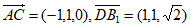 ,
,
所以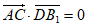 ,
,
所以AC⊥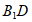 。
。
(Ⅱ)解: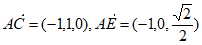 ,
,
设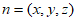 是平面AEC的一个法向量,则
是平面AEC的一个法向量,则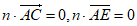 ,
,
即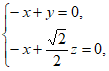
取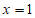 ,则
,则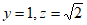 ,即
,即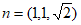 ,
,
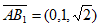 ,
,
点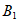 到平面
到平面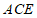 的距离是
的距离是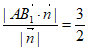 ,
,
所以点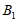 到平面ACE的距离是
到平面ACE的距离是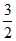 。
。
(III)解: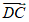 是平面DAE的一个法向量,
是平面DAE的一个法向量,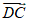 =(0,1,0)。
=(0,1,0)。
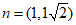 是平面AEC的一个法向量。
是平面AEC的一个法向量。
设二面角D-AE-C的大小是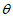 ,则
,则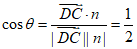 ,
,
所以二面角D-AE-C的大小是60度。
20. 解(I)由题意得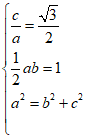
解得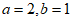
所以椭圆C的方程为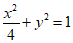
(II)由(I)知,A(2,0),B(0,1)
设P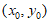 ,则
,则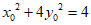
当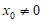 时,
时,
直线PA的方程为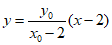
令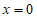 ,得
,得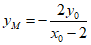 ,从而
,从而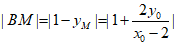 。
。
直线PB的方程为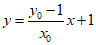 。
。
令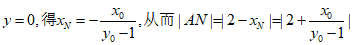 y
y
所以
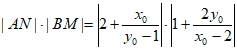
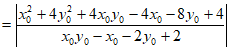
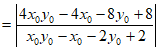
=4。
当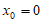 时,
时,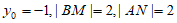 ,
,
所以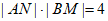 。
。
综上,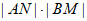 为定值。
为定值。
21. (Ⅰ)证明:因为AD⊥平面PAB,BC∥AD,
所以BC⊥平面PAB,
又因为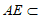 平面PAB,所以AE⊥BC。
平面PAB,所以AE⊥BC。
在△PAB中,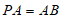 ,E是PB的中点,
,E是PB的中点,
所以AE⊥PB。
又因为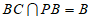 ,所以AE⊥平面PBC,
,所以AE⊥平面PBC,
又因为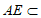 平面AEC,所以平面AEC⊥平面PBC。
平面AEC,所以平面AEC⊥平面PBC。
(Ⅱ)解:因为AD⊥平面PAB,
所以AD⊥AB,AD⊥PA,
又因为PA⊥AB,
所以如图建立空间直角坐标系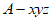 ,
,
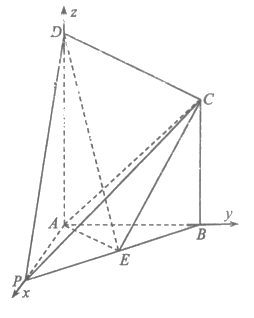
则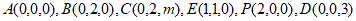 ,
,
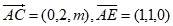 ,
,
设平面AEC的法向量为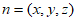 。
。
则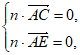
即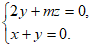 令
令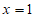 ,则
,则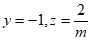 ,
,
于是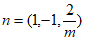 。
。
因为AD⊥平面PAB,所以AD⊥PB,又PB⊥AE,
所以PB⊥平面AED。
又因为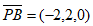 ,
,
所以取平面AED的法向量为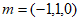 ,
,
所以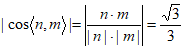 ,
,
即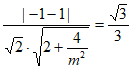 ,解得
,解得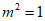 。
。
又因为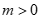 ,所以
,所以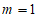 。
。
(Ⅲ)结论:不存在。理由如下:
证明:设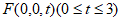 ,
,
当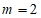 时,
时,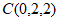 ,
,
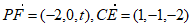 。
。
由PF⊥CE知,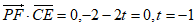 ,这与
,这与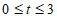 矛盾,
矛盾,
所以,在线段AD上不存在点F,使得PF⊥CE。
22. (Ⅰ)解:由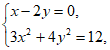 解得
解得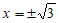 ,
,
所以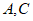 两点的坐标为
两点的坐标为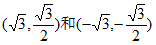 ,
,
所以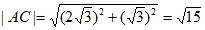 。
。
(Ⅱ)解:①当直线AD的斜率不存在时,
此时易得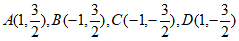 ,
,
所以平行四边形ABCD的面积为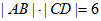 。
。
②当直线AD的斜率存在时,设直线AD的方程为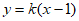 ,
,
将其代入椭圆方程,整理得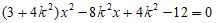 ,
,
设点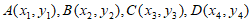 ,
,
则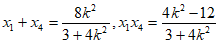 ,
,
连结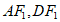 ,
,
则平行四边形ABCD的面积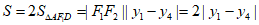 。
。
又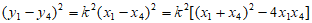
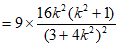 ,
,
所以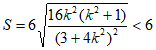 。
。
综上,平行四边形ABCD面积的最大值是6。