本试卷有四道大题,考试时长120分钟,满分100分。
一、本大题(共10小题,共20分,每小题2分)
1. 剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,下列剪纸作品中,是轴对称图形的是( )

2. 下列各式中,能用完全平方公式进行分解的是( )
A. 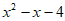 B.
B.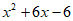
C. 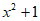 D.
D.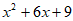
3. 根据下列已知条件,能唯一画出△ABC的是( )
A. AB=3,BC=4,AC=8
B. AB=8,BC=6,∠A=30°
C. ∠A=60°,∠B=45°,AB=4
D. ∠C=90°,AB=8。
4. 把多项式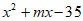 分解因式为(x-5)( x +7),则m的值是( )
分解因式为(x-5)( x +7),则m的值是( )
A. 12 B. -12 C. 2 D. -2
5. n是正整数,计算(-2)2n+1+2×(-2)2n的结果是( )
A. 0 B. 1 C. 22n+1 D. -22n+1
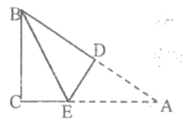
6. 在数学课上,小强提出这样一个问题:如下图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
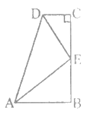
A. 35° B. 45° C. 55° D. 65°
7. 如图,数轴上A,B两点表示的数分别为-1和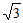 ,点B关于点A的对称点为C,则点C所表示的数为( )
,点B关于点A的对称点为C,则点C所表示的数为( )
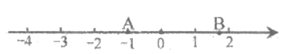
A. -2-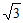 B. -1-
B. -1-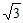 C. -2+
C. -2+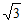 D. 1+
D. 1+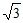
8. 如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标轴建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是( )
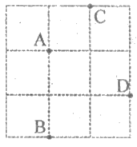
A. 点A B. 点B C. 点C D. 点D
9. 已知∠AOB=45°,点P在∠AOB的内部,P1与P关于OB对称,P2与P关于OA对称,则P1、P2与O三点构成的三角形是( )
A. 直角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
10. 如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )
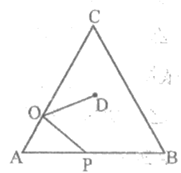
A. 4 B. 5 C. 6 D. 8
二、填空题(共6小题,共18分,每小题3分)
11. 因式分解: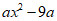 =__________。
=__________。
12. 多项式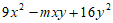 是一个完全平方式,则m的值为__________。
是一个完全平方式,则m的值为__________。
13. 如图,在纸片△ABC中,AC=6,∠A=30°,∠C=90°,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为__________。
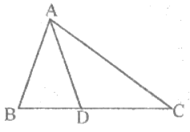
14. 如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C等于__________。
15. 如果满足条件”∠BAC=30°,AC=1,BC=k(k>0)”的△ABC是唯一的,那么k的取值范围是_________。
16. 如图,△ABC中,给出下列四个命题:
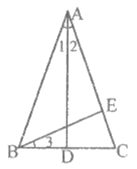
①若AB=AC,AD⊥BC,则∠1=∠2;②若AB=AC,∠1=∠2,则BD=DC;③若AB=AC,BD=DC,则AD⊥BC;④若AB=AC,AD⊥BC,BE⊥AC,则∠1=∠3;其中,真命题的序号是__________。
三、解答题(共8小题,共50分,其中17,18,23题各6分,19题12分,其余各题5分)
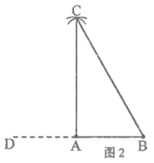
17. 下面是小强同学用尺规作图”作一个角等于60°直角三角形”的过程。
已知:线段AB(如图1)。
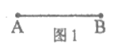
求作△ABC,使∠A=90°,∠B=60°。
作法:如图2。
(1)延长BA至D,使得AD=AB。 (2)分别以点D,点B为圆心,以BD长为半径画弧,两弧交于点C,连接BC。 (3)连接AC。 则△ABC就是所求作的直角三角形。 证明:连接CD, ∵CD=CB=AB, ∴△BCD是等边三角形 (依据1:__________________________________) ∴∠ABC=∠BCD=60°(等边三角形的性质) ∵AB=AD, ∴AC⊥AB。 (依据2:_________________________________) ∴∠BAC=90°。 ∴△ABC就是所求作的直角三角形。 |
根据小强同学的作图,完成下面问题:
(1)写出小强同学证明过程中的依据1和依据2;
(2)参考小强的作图,利用图3再设计一种”作一个角等于60°的直角三角形”的尺规作图方法(保留作图痕迹,不要求写出作法及证明过程)。
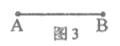
18. 化简下列各式:
(1)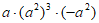 (2)
(2)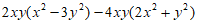
19. 分解因式
(1)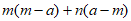 (2)
(2)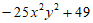
(3)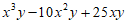 (4)
(4)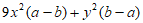
20. 先化简,再求值: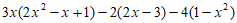 ,其中
,其中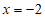 。
。
21. 已知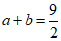 ,
,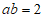 ,求
,求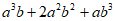 的值。
的值。
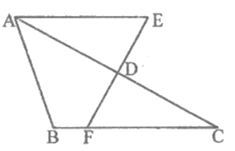
22. 如图,在△ABC中,点D在AC边上,AE∥BC,连接ED并延长交BC于点F,若AD=CD,求证:ED=FD。
23. 如图,在平面直角坐标系xOy中,A(-1,2),B(0,1),C(1,4)。
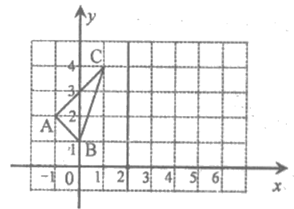
(1)在图中,画出△ABC关于过点(2,0)且垂直于x轴的直线的对称△A1B1C1;并写出点A1的坐标;
(2)若点P(m,n)是△ABC内任意一点,求点P关于过点(2,0)且垂直于x的直线的对称点Q的坐标。
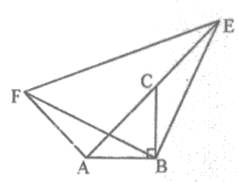
24. 如图,Rt△ABC中,∠ABC=90°,BA=BC,点E在AC的延长线上,且△BCE≌△BAF,求证:△BEF是等于直角三角形。
四、综合题(共2小题,共12分,每道题6分)
25. 小明在学习《整式的乘法》中发现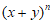 展开式的规律:
展开式的规律:
……
其中第i+1项是 |
(1)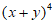 展开式中
展开式中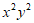 项的系数是_________。
项的系数是_________。
(2)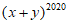 展开式共有_________项。
展开式共有_________项。
(3)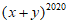 展开式中各项系数之和为_________。
展开式中各项系数之和为_________。
26. 已知:如图,△ABC是等边三角形,点P是外一点,作点B关于射线AP的对称点D,记∠BAP= ,连接BD,CD分别交射线AP与点M,N。
,连接BD,CD分别交射线AP与点M,N。
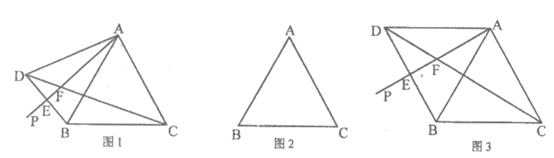
(1)如图1,求∠AFC;
(2)若点A,C,D共线时,补全图2,判断EF与AB的数量关系,并说明理由:
(3)当∠CAD=120°时,直接写出CD,AF与CF的数量关系。
参考答案
一、本大题(共10小题,共20分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | D | C | C | A | A | A | D | D | C |
二、填空题(共6小题,共18分,每小题3分)
11. 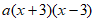 ; 12.
; 12. 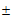 24; 13. 2;
24; 13. 2;
14. 35° 15. 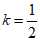 或
或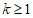 ; 16. ①②③④。
; 16. ①②③④。
三、解答题(共8小题,共50分,其中17,18,23题各6分,19题12分,其余各题5分)
17. (1)依据1:等边三角形定义;
依据2:等腰三角形底边上中线与高线重合。
(2)如下图。

18. (1)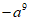 ;(2)
;(2)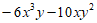
19. (1)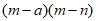 ;(2)(7+5xy)(7-5xy)
;(2)(7+5xy)(7-5xy)
(3)xy(x-5)2;(4)(a–b)(3x+y)(3x–y)。
20. 略
21. 9.
22. 略
23. (1)图略,A1(5,1);(2)Q(4-m,n)。
24. 略
25. (1)6;(2)2021项;(3)22020。
26. (1)60°;(2)EF=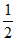 AB;(3)CD=AF+CF。
AB;(3)CD=AF+CF。

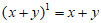
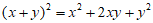
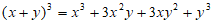
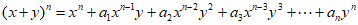
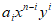 (
(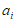 是该项的系数。
是该项的系数。