本试卷有三道大题,考试时长90分钟,满分100分。
一、选择题:共8小题,每小题4分,共32分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知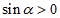 ,且
,且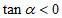 ,则
,则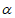 的终边所在的象限是( )
的终边所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 函数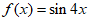 的最小正周期为( )
的最小正周期为( )
A. 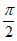 B.
B. 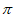 C.
C. 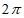 D.
D.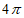
3. 要得到函数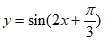 的图象,只需将函数
的图象,只需将函数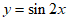 的图象( )
的图象( )
A. 向左平移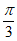 个单位长度 B. 向右平移
个单位长度 B. 向右平移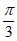 个单位长度
个单位长度
C. 向左平移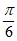 个单位长度 D. 向右平移
个单位长度 D. 向右平移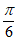 个单位长度
个单位长度
4. 若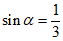 ,则
,则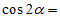 ( )
( )
A. 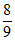 B.
B. 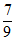 C.
C. 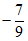 D.
D.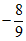
5. 已知向量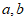 满足
满足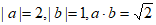 ,则向量
,则向量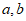 的夹角为( )
的夹角为( )
A. 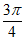 B.
B. 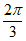 C.
C. 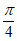 D.
D.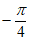
6. 在△ABC中,若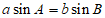 ,则△ABC的形状一定是( )
,则△ABC的形状一定是( )
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D. 等腰三角形或直角三角形
7. sin20°cos10°-cos160°sin10°=( )
A. 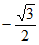 B.
B. 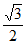 C.
C. 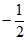 D.
D.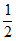
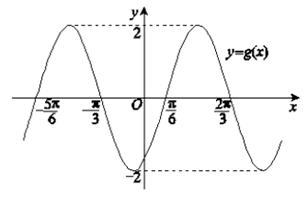
8. 函数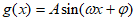 的图像如下图所示,其中
的图像如下图所示,其中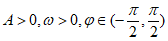 ,则
,则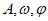 的值依次为( )
的值依次为( )
A. 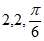 B.
B. 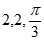 C.
C. 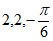 D.
D.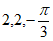
二、填空题:共8小题,每小题4分,共32分。
9. 若角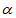 的终边经过点
的终边经过点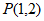 ,则
,则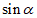 等于__________。
等于__________。
10. 设向量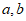 的长度分别为4和3,它们的夹角为60°,则
的长度分别为4和3,它们的夹角为60°,则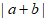 等于__________。
等于__________。
11. 函数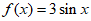 的最大值为___________。
的最大值为___________。
12. 设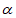 是第一象限角,
是第一象限角,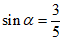 ,则
,则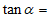 __________;
__________;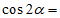 ___________。
___________。
13. 若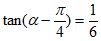 ,则
,则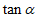 =____________。
=____________。
14. 设向量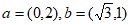 ,则
,则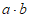 =_________;向量
=_________;向量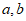 的夹角等于________。
的夹角等于________。
15. 在△ABC中,三个内角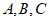 的对边分别是
的对边分别是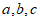 ,若
,若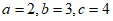 ,则
,则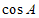 =___________。
=___________。
16. 在△ABC中,三个内角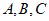 的对边分别是
的对边分别是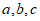 ,若
,若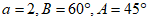 ,则b=__________,△ABC的面积是___________。
,则b=__________,△ABC的面积是___________。
三、解答题:共4小题,每小题9分,共36分。解答应写出文字说明、演算步骤或证明过程。
17. 已知函数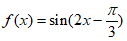 。
。
(Ⅰ)求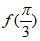 的值;
的值;
(Ⅱ)求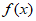 的最小正周期;
的最小正周期;
(Ⅲ)求函数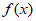 的单调递增区间。
的单调递增区间。
18. 在△ABC中,角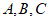 所对的边分别为
所对的边分别为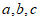 ,已知
,已知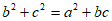 。
。
(Ⅰ)求A的大小;
(Ⅱ)如果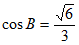 ,
,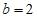 ,求△ABC的面积。
,求△ABC的面积。
19. 已知函数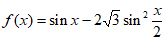 。
。
(Ⅰ)求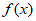 的最小正周期;
的最小正周期;
(Ⅱ)求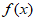 在区间
在区间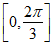 上的最小值。
上的最小值。
20. 在△ABC中,角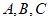 的对边分别为
的对边分别为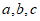 ,且
,且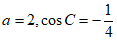 。
。
(Ⅰ)求sinC的值;
(Ⅱ)如果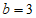 ,求c的值;
,求c的值;
(Ⅲ)如果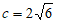 ,求
,求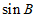 的值。
的值。
【试题答案】
一、选择题:共8小题,每小题4分,共32分。
1. B 2. A 3. C 4. B 5. C 6. B 7. D 8. D
二、填空题:共8小题,每小题4分,共32分。
9. 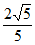 10.
10. 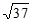 11. 3 12.
11. 3 12. 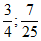 13.
13.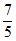
14. 2;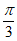 15.
15. 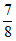 16.
16. 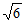 ;
;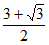
三、解答题:共4小题,每小题9分,共36分。解答应写出文字说明、演算步骤或证明过程。
17. 解:(Ⅰ)由已知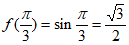 。
。
(Ⅱ)函数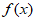 的最小正周期为
的最小正周期为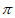 。
。
(Ⅲ)由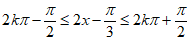 ,得
,得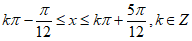 。
。
则函数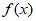 的单调递增区间为
的单调递增区间为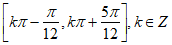 。
。
18. (Ⅰ)60°;(Ⅱ)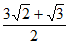 。
。
19. 解:(Ⅰ)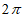 ;(Ⅱ)
;(Ⅱ)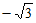 。
。
20. (Ⅰ)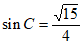 ;
;
(Ⅱ)由余弦定理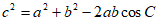 ,
,
得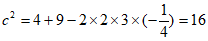 ,
,
解得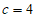 。
。
(Ⅲ)(方法一)由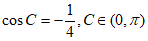 ,得
,得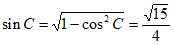 。
。
由正弦定理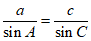 ,得
,得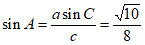 ,
,
所以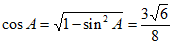 。
。
因为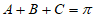 ,
,
所以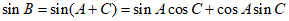
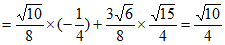 。
。
(方法二)由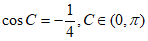 ,得
,得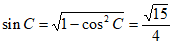 。
。
由余弦定理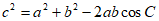 ,
,
得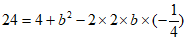 ,
,
解得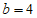 ,或
,或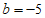 (舍)。
(舍)。
由正弦定理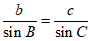 ,得
,得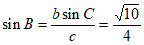 。
。
