本试卷满分120分,考试时间100分钟
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合A={x|x(x+1)≤0},集合B={x|-1<x<1},则A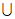 B=( )
B=( )
A. {x|-1≤x≤1} B. {x|-l<x≤0}
C. {x|-1≤x<1} D. {x|0<x<1}
2. 命题”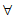 x>0,
x>0,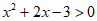 “的否定是( )
“的否定是( )
A. 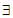 x>0,
x>0,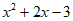 ≤0 B.
≤0 B. 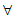 x>0,
x>0,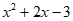 ≤0
≤0
C. 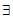 x<0,
x<0,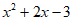 ≤0 D.
≤0 D. 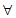 x<0,
x<0,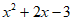 ≤0
≤0
3. 已知a,b∈R,则”a>b”是”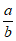 >1″的( )
>1″的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4. 已知集合A={x|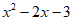 <0},B={x|-1<x<m},若x∈A是x∈B的充分不必要条件,则实数m的取值范围为( )
<0},B={x|-1<x<m},若x∈A是x∈B的充分不必要条件,则实数m的取值范围为( )
A. (3,+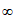 ) B. (-1,3)
) B. (-1,3)
C. [3,+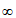 ) D. (-1,3]
) D. (-1,3]
5. 方程组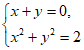 的解集是( )
的解集是( )
A. {(1,-1),(-1,1)} B. {(1,1),(-1,-1)}
C. {(2,-2),(-2,2)} D. {(2,2),(-2,-2)}
6. 已知a,b是方程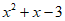 =0的两个实数根,则
=0的两个实数根,则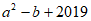 的值是( )
的值是( )
A. 2023 B. 2021 C. 2020 D. 2019
7. 下列函数中,在区间(1,+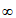 )上为增函数的是( )
)上为增函数的是( )
A. y=-3x-1 B. y=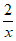 C. y=
C. y=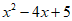 D. y=|x-1|+2
D. y=|x-1|+2
8. 若不等式|x-3|+|x-4|<a的解集不为空集,则a的取值范围是( )
A. a≤1 B. a≥1 C. a<1 D. a>1
9. 已知a>0,b>0,若a+b=4,则( )
A. 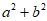 有最小值 B.
有最小值 B. 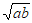 有最小值
有最小值
C. 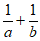 有最大值 D.
有最大值 D. 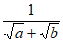 有最大值
有最大值
10. 设函数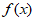 在(-
在(-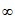 ,+
,+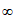 )上有意义,对任意的x,y∈R且x≠y,都有
)上有意义,对任意的x,y∈R且x≠y,都有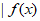 –
–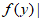 <|x-y|,并且函数
<|x-y|,并且函数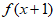 的对称中心是(-1,0),若函数
的对称中心是(-1,0),若函数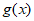 –
–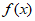 =x,则不等式g
=x,则不等式g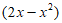 +g
+g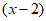 <0的解集是( )
<0的解集是( )
A. (-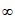 ,1)
,1)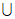 (2,+
(2,+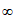 ) B. (1,2)
) B. (1,2)
C. (-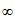 ,-1)
,-1)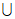 (2,+
(2,+ ) D. (-1,2)
) D. (-1,2)
二、填空题共6小题,每小题5分,共30分。
11. 若函数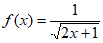 ,则
,则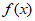 的定义域为_________。
的定义域为_________。
12. 已知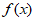 是定义在R上的奇函数,且当x>0时,
是定义在R上的奇函数,且当x>0时,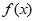 =
=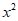 ,则
,则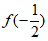 =________。
=________。
13. 写出一个使得命题”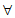 x∈R,
x∈R,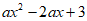 >0恒成立”是假命题的实数a的值________:
>0恒成立”是假命题的实数a的值________:
14. 某餐厅经营盒饭生意,每天的房租、人员工资等固定成本为200元,每盒盒饭的成本为15元,销售单价与日均销售量的关系如下表:
单价/元 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
日销售量/盒 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
根据以上数据,当这个餐厅利润(利润=总收入-总成本)最大时,每盒盒饭定价为________元。
15. 函数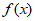 =
=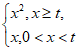 (t>0)是区间(0,+
(t>0)是区间(0,+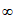 )上的增函数,则t的取值范围是________。
)上的增函数,则t的取值范围是________。
16. 几位同学在研究函数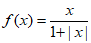 (x∈R)时给出了下面几个结论:
(x∈R)时给出了下面几个结论:
①函数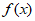 的值域为(-1,1);
的值域为(-1,1);
②若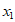 ≠
≠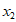 ,则一定有
,则一定有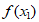 ≠
≠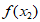 ;
;
③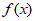 在(0,+
在(0,+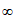 )上是增函数;
)上是增函数;
④若规定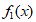 =
=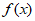 ,且对任意正整数n都有:
,且对任意正整数n都有: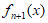 =
=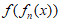 ,则
,则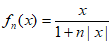 对任意n∈N*恒成立。
对任意n∈N*恒成立。
上述结论中正确结论的序号为_________。
三、解答题共5小题,共50分。解答应写出文字说明、演算步骤或证明过程。
17. (本小题8分)
设全集U=R,集合A=(-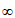 ,-1]
,-1]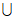 [4,+
[4,+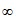 ),B=(-
),B=(-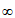 ,1]。求:
,1]。求:
(1)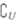 (A
(A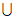 B);
B);
(2)记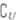 (A
(A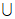 B)=M,N={x|a-1≤x≤-2a},且M
B)=M,N={x|a-1≤x≤-2a},且M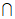 N=N,求a的取值范围。
N=N,求a的取值范围。
18. (本小题10分)
定义在R上的函数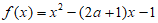 (a∈R)。
(a∈R)。
(1)若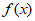 为偶函数且
为偶函数且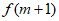 >
>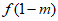 ,求实数m的取值范围;
,求实数m的取值范围;
(2)若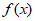 不是偶函数且在区间[-1,2]上不单调,求实数a的取值范围。
不是偶函数且在区间[-1,2]上不单调,求实数a的取值范围。
19. (本小题10分)
记关于x的方程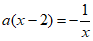 在区间(0,3]上的解集为A,若A至多有2个不同的子集,求实数a的取值范围。
在区间(0,3]上的解集为A,若A至多有2个不同的子集,求实数a的取值范围。
20. (本小题10分)
已知不等式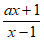 <0(a∈R)。
<0(a∈R)。
(1)当a=2时,解这个不等式;
(2)若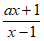 ≤1-x对
≤1-x对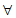 x∈(-
x∈(-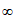 ,0)恒成立,求实数a的最大值。
,0)恒成立,求实数a的最大值。
21. (本小题12分)
已知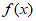 是定义在R上的单调递减函数,对任意实数m,n都有
是定义在R上的单调递减函数,对任意实数m,n都有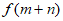 =
=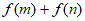 。函数
。函数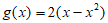 。定义在R上的单调递增函数
。定义在R上的单调递增函数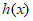 的图像经过点A(0,0)和点B(2,2)。
的图像经过点A(0,0)和点B(2,2)。
(1)判断函数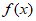 的奇偶性并证明;
的奇偶性并证明;
(2)若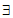 t∈[-1,2],使得
t∈[-1,2],使得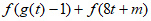 <0(m为常实数)成立,求m的取值范围;
<0(m为常实数)成立,求m的取值范围;
(3)设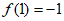 ,F1(x)=f(x)-x,F2(x)=g(x),F3(x)=h(x)-h(2-x),
,F1(x)=f(x)-x,F2(x)=g(x),F3(x)=h(x)-h(2-x),
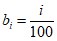 (i=0,1,2…,100)。若
(i=0,1,2…,100)。若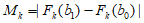 +
+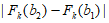 +…+
+…+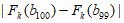 (k=1,2,3),比较M1,M2,M3的大小并说明理由。
(k=1,2,3),比较M1,M2,M3的大小并说明理由。
参考答案
1. C
2. A
3. D
当a=0,b=-l时,满足a>b,但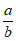 <l;
<l;
当a=-2,b=-1时,满足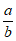 >1,但a<b。
>1,但a<b。
所以”a>b”是”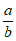 >l”的既不充分也不必要条件。
>l”的既不充分也不必要条件。
4. A
5. A
6. A
7. D
8. D
9. A
10. A
11. 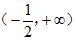
12. 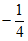 。
。
13. -1(答案不唯一,只需a∈(-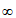 ,0)
,0)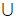 [3,+
[3,+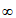 ))。
))。
14. 21.5。
15. [1,+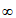 )。
)。
16. ①②③④.
17. (1)由题意知,A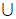 B=(-
B=(-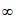 ,1]
,1]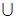 [4,+
[4,+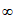 ),
),
又全集U=R,所以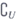 (A
(A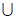 B)=(1,4)。
B)=(1,4)。
(2)由(1)得M=(1,4),由M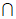 N=N得N
N=N得N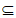 M。
M。
①当N=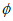 时,有a-1>-2a,所以a>
时,有a-1>-2a,所以a>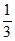 ;
;
②当N≠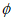 时,有
时,有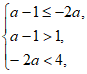 此不等式组无解。
此不等式组无解。
综上,a的取值范围是(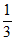 ,+
,+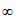 )。
)。
18. (1)因为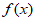 为偶函数,所以
为偶函数,所以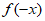 =
=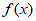 恒成立,
恒成立,
即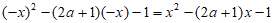 恒成立,所以
恒成立,所以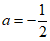 ,
,
所以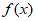 =
=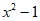 ,其图像是开口向上的抛物线且关于y轴对称,
,其图像是开口向上的抛物线且关于y轴对称,
因为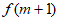 >
>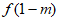 ,所以
,所以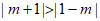 ,所以m>0。
,所以m>0。
所以实数m的取值范围是(0,+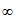 )。
)。
(2)依题意,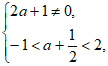 所以
所以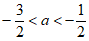 或
或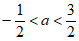 ,
,
所以实数a的取值范围是(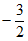 ,
,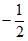 )
)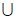 (
(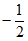 ,
,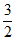 )。
)。
19. 因为A至多有2个不同的子集,所以A至多有1个元素。
因为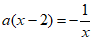 ,所以
,所以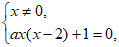 所以
所以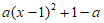 =0,
=0,
所以原题等价于函数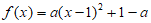 在区间(0,3]上至多有1个零点。
在区间(0,3]上至多有1个零点。
①当a=0时,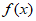 =1在区间(0,3]上无零点,符合题意;
=1在区间(0,3]上无零点,符合题意;
②当a>0时,抛物线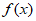 =
=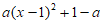 开口向上,对称轴为x=1,
开口向上,对称轴为x=1,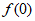 =1,
=1,
所以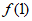 =1-a≥0,所以0<a≤1;
=1-a≥0,所以0<a≤1;
③当a<0时,抛物线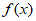 =
=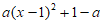 开口向下,对称轴为x=1,
开口向下,对称轴为x=1,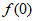 =1=
=1=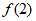 ,
,
所以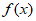 在(0,3]上至多有一个零点,符合题意。
在(0,3]上至多有一个零点,符合题意。
综上,实数a的取值范围是(-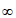 ,1]。
,1]。
20. (1)当a=2时,原不等式可化为(2x+1)(x-1)<0。
所以不等式解集为(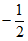 ,1)。
,1)。
(2)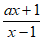 ≤l-x对
≤l-x对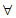 x∈(-
x∈(-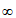 ,0)恒成立,
,0)恒成立,
等价于ax+1≥(x-1)(1-x)对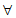 x∈(-
x∈(-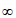 ,0)恒成立,
,0)恒成立,
等价于(a-2)x≥-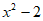 对
对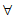 x∈(-
x∈(-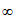 ,0)恒成立,
,0)恒成立,
等价于a-2≤-x-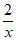 对
对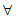 x∈(-
x∈(-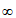 ,0)恒成立。
,0)恒成立。
因为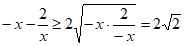 ,当且仅当-x=
,当且仅当-x=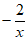 即
即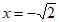 时等号成立,
时等号成立,
所以a-2≤2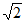 ,所以a≤2
,所以a≤2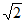 +2,
+2,
所以实数a的最大值为2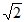 +2。
+2。
21. (1)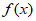 是R上的奇函数。证明如下:
是R上的奇函数。证明如下:
因为任意实数m,n都有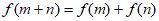 ,
,
所以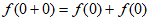 ,所以
,所以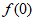 =0,
=0,
从而对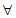 x∈R,恒有
x∈R,恒有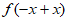 =
=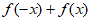 ,所以
,所以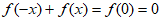 ,
,
所以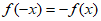 ,所以
,所以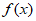 为奇函数。
为奇函数。
(2)由(1)知,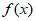 为R上单调递减的奇函数,
为R上单调递减的奇函数,
由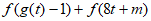 <0得
<0得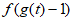 <
<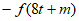 =
=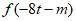 ,
,
所以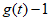 >-8t-m,
>-8t-m,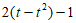 >
>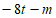 ,
,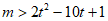 。
。
令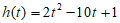 ,则
,则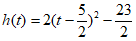 。
。
当t∈[-l,2]时,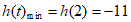 。
。
所以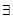 t∈[-l,2],使得
t∈[-l,2],使得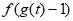 +
+ <0成立,
<0成立,
等价于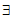 t∈[-1,2],使得m>h(t)成立,
t∈[-1,2],使得m>h(t)成立,
所以m>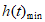 =-11,所以m的取值范围是(-11,+∞)。
=-11,所以m的取值范围是(-11,+∞)。
(3)依题意,易证F1(x)= 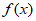 -x在R上单调递减,
-x在R上单调递减,
所以M1=|F1(b1)-F1(b0)|+| F1(b2)- F1(b1)|+…+| F1(b100)-F1(b99)|
= F1(b0)- F1(b1)+ F1(b1)- F1(b2)+…+ F1(b99)- F1(b100)
= F1(b0)- F1(b100)= F1(0)-Fl(1)=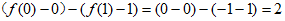 。
。
因为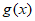 =2
=2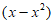 =-2
=-2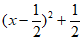 在[0,
在[0,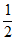 ]单调递增,在[
]单调递增,在[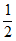 ,1]单调递减,
,1]单调递减,
所以M2=|F2(b1)- F2(b0)|+| F2(b2)- F2(b1)|+…+| F2(b100)- F2(b99)|
= F2(b1)- F2(b0)+ F2(b2)- F2(b1)+…+ F2(b50)- F2(b49)
+F2(b50)- F2(b51)+ F2(b51)- F2(b52)+…+ F2(b99)- F2(b100)
=-F2(b0)+F2(b50)+ F2(b50)- F2(b100)=- F2(0)+ F2(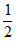 )+F2(
)+F2(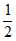 )-F2(1)=-0+
)-F2(1)=-0+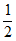 +
+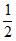 -0=1。
-0=1。
由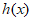 在R上单调递增,易证F3(x)=h(x)-h(2-x)在R上单调递增,
在R上单调递增,易证F3(x)=h(x)-h(2-x)在R上单调递增,
所以M3=|F3(b1)- F3(b0)|+| F3(b2)- F3(b1)|+…+| F3(b100)- F3(b99)|
= F3(b1)- F3(b0)+ F3(b2)- F3(b1)+…+ F3(b100)- F3(b99)
= F3(b100)- F3(b0)=F3(1)-F3(0)=(h(1)-h(2-1))-(h(0)-h(2))=0-(0-2)=2,
所以M1=M3>M2。
