(本试卷满分120分,考试时间100分钟)
一、选择题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 在复平面内,复数1+i的共轭复数所对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 直线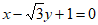 的倾斜角的度数是( )
的倾斜角的度数是( )
A. 30° B. 45° C. 60° D. 90°
3. 点(0,1)到直线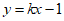 距离的最大值为( )
距离的最大值为( )
A. 1 B. 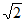 C.
C. 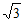 D. 2
D. 2
4. 直线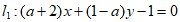 与
与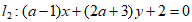 互相垂直,则实数a的值为( )
互相垂直,则实数a的值为( )
A. -1 B. 1 C. -1或1 D. 以上都不对
5. 已知向量a=(1,x,-2),b=(0,l,2),c=(1,0,0),若a,b,c共面,则x等于( )
A. -1 B. l C. 1或-1 D. 1或0
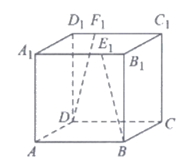
6. 如图,ABCD-A1B1C1D1是正方体,B1E1=D1F1=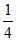 A1B1,则BE1与DF1所成角的余弦值是( )
A1B1,则BE1与DF1所成角的余弦值是( )
A. 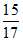 B.
B. 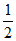 C.
C. 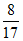 D.
D.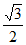
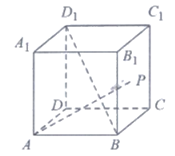
7. 如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
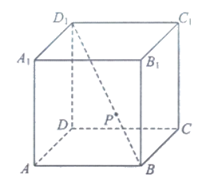
A. 3个 B. 4个 C. 5个 D. 6个
8. 设复数z满足|z-1-i|=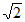 ,则|z|的最大值为( )
,则|z|的最大值为( )
A. 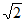 B. 2 C. 2
B. 2 C. 2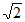 D. 4
D. 4
9. 通过求两个向量的夹角,可以求两条直线的夹角。已知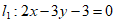 ,
,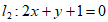 ,则l1,l2夹角的余弦值是( )
,则l1,l2夹角的余弦值是( )
A. 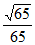 B.
B. 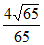 C.
C. 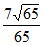 D.
D.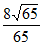
10. 已知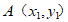 ,
,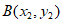 是不同的两点,点C(cos
是不同的两点,点C(cos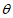 ,sin
,sin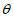 ),且
),且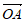 ·
·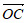 =
=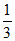 ,
,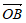 ·
·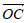 =
=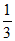 ,则直线AB与圆
,则直线AB与圆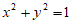 的位置关系是( )
的位置关系是( )
A. 相离 B. 相切
C. 相交 D. 以上三种情况都有可能
二、填空题共5小题,每小题5分,共25分。
11. 复数z=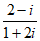 ,则|z|=_________。
,则|z|=_________。
12. 已知ABCD为平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),则顶点D的坐标为__________。
13. 已知圆C: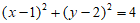 与直线
与直线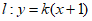 ,则圆心C的坐标为_________,若圆C关于直线l对称,则k=___________。
,则圆心C的坐标为_________,若圆C关于直线l对称,则k=___________。
14. 直线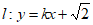 与圆
与圆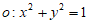 相交于A,B两点,当△AOB的面积达到最大时,k=__________。
相交于A,B两点,当△AOB的面积达到最大时,k=__________。
15. 在正方体ABCD-A1B1C1D1中,点P是侧面B1C1CB内(不包含边界)的一个动点,且AP⊥D1B,点H在棱D1D上运动,则二面角H-AC-P的余弦值的取值范围是________。
三、解答题共5小题,共45分。解答应写出文字说明、演算步骤或证明过程。
16. (本小题8分)
已知复数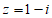 (i是虚数单位)。
(i是虚数单位)。
(1)求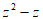 ;
;
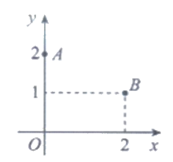
(2)如图,复数z1,z2在复平面上的对应点分别是A,B,求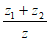 。
。
17. (本小题8分)
已知圆C的圆心在y轴上,且过(0,0),(0,2)两点。
(1)求圆C的方程;
(2)若圆C与圆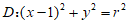 有公共点,求r的取值范围。
有公共点,求r的取值范围。
18. (本小题10分)
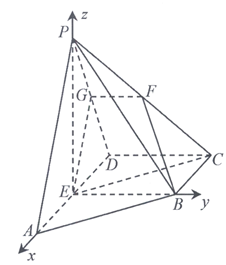
在四棱锥P-ABCD中,底面ABCD为直角梯形。BC∥AD,∠ADC=90°,BC=CD=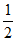 AD=1,E为线段AD的中点。PE⊥底面ABCD,且PE=
AD=1,E为线段AD的中点。PE⊥底面ABCD,且PE=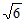 ,点F是棱PC的中点,平面BEF与校PD相交于点G。
,点F是棱PC的中点,平面BEF与校PD相交于点G。
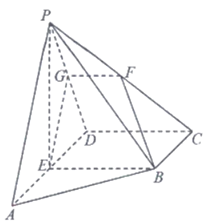
(1)求证:BE∥FG;
(2)求直线PB与平面BEF所成角的正弦值;
(3)设H为PB中点,DH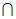 平面BEF=M,求BM的长。
平面BEF=M,求BM的长。
19. (本小题10分)
已知圆M: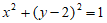 ,Q是x轴上的动点,QA,QB分别切圆M于A,B两点。
,Q是x轴上的动点,QA,QB分别切圆M于A,B两点。
(1)若Q(1,0),求切线QA,QB的方程;
(2)求四边形QAMB面积的最小值;
(3)若|AB|=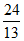 ,求直线MQ的方程。
,求直线MQ的方程。
20. (本小题9分)
已知集合Rn={(x1,x2,…,xn)|xi∈R,i=1,2. …,n}(n≥1),定义Rn上两点A(a1,a2,…,an),B(b1,b2,…,bn)的距离d(A,B)=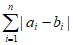 。
。
(1)当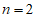 时,以下命题正确的有_________(不需证明);
时,以下命题正确的有_________(不需证明);
①若A(1,2),B(4,6),则d(A,B)=7;
②在△ABC中,若∠C=90°,则[d(A,C)]2+[d(C,B)]2=[d(A,B)]2;
③在△ABC中,若d(A,B)=d(A,C),则∠B=∠C;
(2)当n=2时,证明R2中任意三点A,B,C之间的距离满足d(A,B)≤d(A,C)+d(C,B);
(3)当n=3时,设A(0,0,0),B(4,4,4),P(x,y,z),其中x,y,z∈Z,d(A,P)+d(P,B)=d(A,B)。
求满足条件的P点的个数n,并证明从这n个点中任取11个点,其中必存在4个点,它们共面或以它们为顶点的三棱锥体积不大于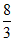 。
。
参考答案
1. D
2. A
3. D
4. C
5. A
6. A
7. B
设长方体的棱长为a,建立空间直角坐标系,如图所示。
则D(0,0,0),D1(0,0,a),C1(0,a,a),C(0,a,0),B(a,a,0),B1(a,a,a),A(a,0,0),A1(a,0,a),
P(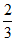 a,
a,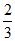 a,
a,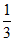 a),
a),
则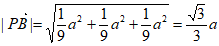 ,
,
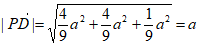 ,
,
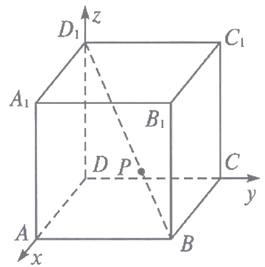
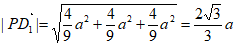 ,
,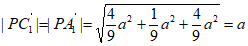 ,
,
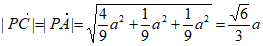 ,
,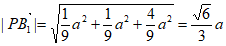
故有4个不同的取值,答案为B。
8. C
9. A
10. C
11. 1。
12. (5,13,-3)。
提示:AC的中点坐标为(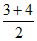 ,
,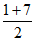 ,
,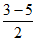 )。因为AC的中点同时为BD的中点,
)。因为AC的中点同时为BD的中点,
所以D的坐标为(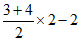 ,
,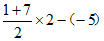 ,
,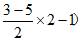 ,即(5,13,-3)。
,即(5,13,-3)。
13. (1,2);1。
14. ±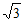 。
。
15. [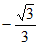 ,
,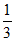 ]。
]。
16.
(1)因为z=1-i,
所以 。
。
(2)因为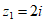 ,
,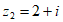 ,
,
所以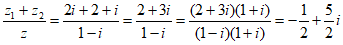 。
。
17.
(1)因为圆C的圆心在y轴上,所以设圆C的方程为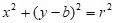 。
。
因为圆C过(0,0),(0,2)两点,所以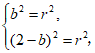 解得
解得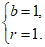
所以圆C的方程是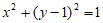 。
。
(2)r的取值范围为[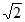 -1,
-1,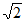 +1]
+1]
18.
(1)因为E为AD中点,所以DE=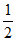 AD=1。
AD=1。
又因为BC=1,所以DE=BC。
在梯形ABCD中,DE∥BC,所以四边形BCDE为平行四边形。所以BE∥CD。
又因为BE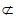 平面PCD,且CD
平面PCD,且CD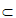 平面PCD,所以BE∥平面PCD。
平面PCD,所以BE∥平面PCD。
因为BE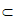 平面BEF,平面BEF
平面BEF,平面BEF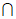 平面PCD=FG,
平面PCD=FG,
所以BE∥FG。
(2)因为PE⊥平面ABCD,
且AE,BE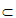 平面ABCD,
平面ABCD,
所以PE⊥AE,且PE⊥BE。
因为四边形BCDE为平行四边形,∠ADC=90°,
所以AE⊥BE。
以E为坐标原点,如图建立空间直角坐标系E-xyz。
则E(0,0,0),A(1,0,0),B(0,1,0),C(-1,1,0),D(-1,0,0)。
设P(0,0,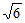 ),
),
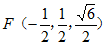 。
。
所以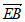 =(0,1,0),
=(0,1,0),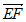 =(
=(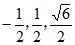 ),
),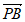 =(0,1,
=(0,1,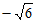 )。
)。
设平面BEF的法向量为n=(x,y,z),
则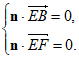 即
即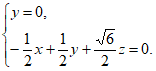
令x=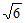 ,则z=1,所以n=(
,则z=1,所以n=(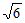 ,0,1)。
,0,1)。
所以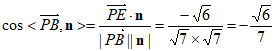 。
。
所以直线PB与平面BEF的所成角的正弦值为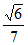 。
。
(3)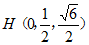 ,所以
,所以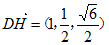 ,因为M
,因为M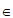 线段DH,所以存在
线段DH,所以存在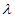 ∈[0,1],
∈[0,1],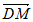 =
=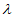
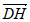 ,所以
,所以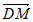 =(
=(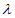 ,
,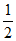
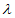 ,
,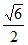
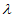 ),所以
),所以
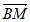 =
=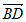 +
+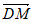 =(
=(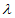 -1,
-1,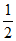
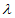 -1,
-1,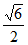
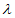 )
)
因为M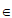 平面BEF
平面BEF
所以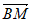 ·n=0,所以
·n=0,所以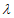 =
=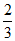 ,|BM|=
,|BM|=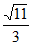
19. (1)设过点Q的圆M的切线方程为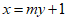 ,
,
则圆心M到切线的距离为1,
所以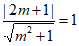 ,所以
,所以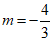 或0,
或0,
所以QA,QB的方程分别为3x+4y-3=0和x=1。
(2)因为MA⊥AQ,所以SMAQB=|MA|·|QA|=|QA|=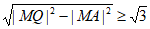 。
。
所以四边形QAMB面积的最小值为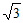 。
。
(3)设AB与MQ交于P,则MP⊥AB,MB⊥BQ,
所以|MP|=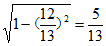 。
。
在Rt△MBQ中,|MB|2=|MP||MQ|,
即1=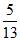 |MQ|,所以|MQ|=
|MQ|,所以|MQ|=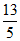 ,所以
,所以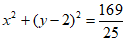 。
。
设Q(x,0),则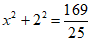 ,所以
,所以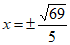 ,所以
,所以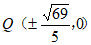 ,
,
所以MQ的方程为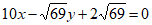 或
或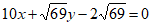 。
。
20. (1)①。
d(A,B)=|a1–b1|+|a2–b2|=|a1–c1+c1–b1|+|a2–c2+c2–b2|
(2)≤|a1–c1|+|c1–b1|+|a2–c2|+|c2–b2|
=|a1–c1|+|a2–c2|+|c1–b1|+|c2–b2|=d(A,C)+d(C,B)
(3)首先确定满足条件的点P有125个,即n=125,它们分布在4×4×4的正方体格点上。
下证从这125个点中任取11个点,必有4个点共面或构成的三棱锥体积不大于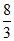 。
。
记选出的11个点为P1,P2,…,P11。若其中有4个点共面则得证;否则,记Si={(x,y,i-1)|0≤x≤4,0≤y≤4,x,y∈Z},i=1,2,3,4,5,则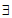 k∈{l,2,3,4,5}使得这11个点中的3个点(不妨记作P1,P2,P3)属于Sk(抽屉原理),此时
k∈{l,2,3,4,5}使得这11个点中的3个点(不妨记作P1,P2,P3)属于Sk(抽屉原理),此时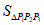 ≤8。
≤8。
当k=1时,若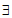 P4∈S2,则
P4∈S2,则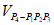 ≤
≤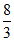 ,得证;否则,P4,…,P11这8个点分布在S3,S4,S5中,可以证明S3或S5中含有这8个点中的3个点(不妨记作P4,P5,P6)且
,得证;否则,P4,…,P11这8个点分布在S3,S4,S5中,可以证明S3或S5中含有这8个点中的3个点(不妨记作P4,P5,P6)且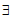 P7∈S4,则
P7∈S4,则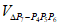 ≤
≤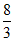 。k=5时同理可证。
。k=5时同理可证。
当k=2,3,4时,仿照上面的证明过程易证。
