一、选择题共10小题,每题3分,共30分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 500米口径球面射电望远镜,简称FAST,是世界上最大的单口径球面射电望远镜,被誉为”中国天眼”。2018年4月18日,FAST望远镜首次发现的毫秒脉冲星得到国际认证,新发现的脉冲星自转周期为0.00519秒,是至今发现的射电流量最弱的高能毫秒脉冲星之一。将0.00519用科学记数法表示应为( )
A. 0.519×10-2 B. 5.19×10-3
C. 51.9×10-4 D. 5.19×10-4
2. 如果把分式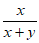 中的x,y都扩大到原来的5倍,那么分式的值( )
中的x,y都扩大到原来的5倍,那么分式的值( )
A. 扩大到原来的25倍 B. 扩大到原来的5倍
C. 值不变 D. 缩小为原来的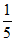
3. 下列运算结果为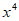 的是( )
的是( )
A. 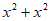 B.
B. 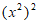 C.
C. 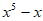 D.
D.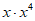
4. 一个多边形的每一个外角都等于60°,那么这个多边形的内角和为( )
A. 1260° B. 1080° C. 720° D. 360°
5. 下列等式由左边至右边的变形中,属于因式分解的是( )
A. 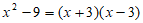 B.
B.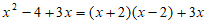
C. 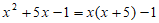 D.
D.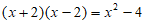
6. 若x=3是分式方程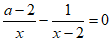 的解,则a的值是( )
的解,则a的值是( )
A. 5 B. -5 C. 3 D. -3
7. 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
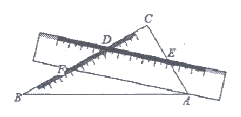
A. 40° B. 45° C. 50° D. 10°
8. 将图甲中阴影部分的小长方形变换到图乙位置,根据两个图形的面积关系可以得到一个关于a、b的恒等式为( )
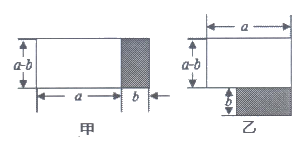
A. 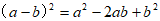 B.
B.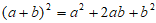
C. 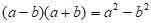 D.
D.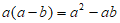
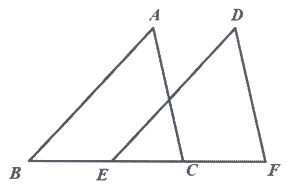
9. 如图,点F,B,E,C在同一条直线上,点A,D在直线BE的两侧,AC∥DF,CE=FB,添加下列哪个条件后,仍不能判定出△ABC≌△DEF( )
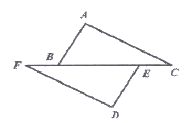
A. AB=DE B. AB∥DE C. ∠A=∠D D. AC=DF
10. 在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2。当AD-AB=2时,S2-S1的值为( )
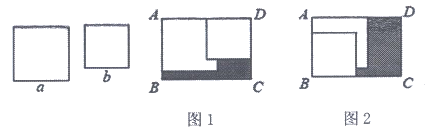
A. 2a B. 2b C. 2a-2b D. -2b
二、填空题共8小题,每题2分,共16分。
11. 当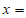 _________时,分式
_________时,分式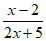 的值为0。
的值为0。
12. 分解因式: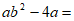 _________。
_________。
13. 化简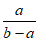 +
+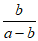 的结果是_________。
的结果是_________。
14. 若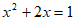 ,则
,则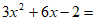 ___________。
___________。
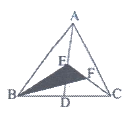
15. 如图,在△ABC中,已知点D、E、F分别为BC、AD、CE的中点,且S△ABC=8cm2,则S△BEF=__________cm2。
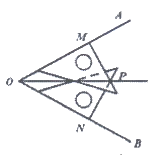
16. 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP。可判定△OMP≌△ONP,依据是__________(请从”SSS、SAS、AAS、ASA、HL”中选择一个填入)。
17. 已知BD,CE是△ABC的高,且BD,CE所在直线相交所成的4个角中,有一个角的度数是45°,则∠BAC的度数为__________。
18. 我们把正n边形(n>3)的各边三等分,分别以居中的那条线段为一边向外作正n边形,并去掉居中的那条线段,得到一个新的图形叫做正n边形的”扩展图形”,并将它的边数记为an。如图1,将正三角形进行上述操作后得到其”扩展图形”,且a3=12。
图2、图3分别是正五边形、正六边形的”扩展图形”。
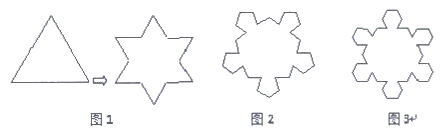
(1)已知a3=12,a4=20,a5=30,则图3中a6=__________;
(2)已知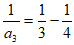 ,
,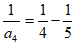 ,
,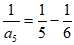 ,……,
,……,
且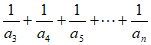 =
=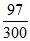 ,则
,则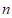 =_________。
=_________。
三、解答题共9小题,19题、20题每小题3分,21题、22题每题5分,23题至25题每题6分,26题、27题每题7分,共54分。解答应写出文字说明、演算步骤或证明过程。
19. 计算:
(1)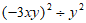 (2)
(2)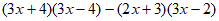
20. 计算:
(1)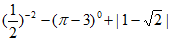
(2)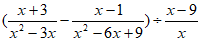
21. 先化简,再求值:(1+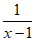 )÷
)÷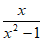 ,其中x=-2。
,其中x=-2。
22. 解分式方程: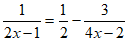 。
。
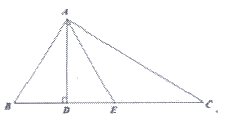
23. 已知:如图,在△ABC中,∠BAC=90°,AD⊥BC于D,AE平分∠DAC,∠B=62°,求∠AEC的度数。
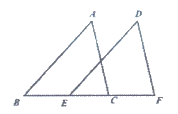
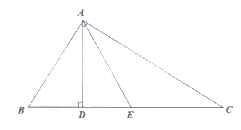
24. 如图,点B,E,C,F在一条直线上。∠B=∠DEF,∠ACB=∠F,BE=CF。求证:△ABC≌△DEF。
25. 在”新冠疫情”期间,某小区物业为预防业主感染病毒,购买A型和B型两种3M口罩,购买A型3M口罩花费了2500元,购买B型3M口罩花费了2000元,且购买A型3M口罩数量是购买B型3M口罩数量的2倍,已知购买一个B型3M口罩比购买一个A型3M口罩多花3元。求该物业购买A型3M口罩的单价为多少元?
26. 在平面直角坐标系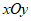 中,我们称横、纵坐标都是整数的点为整点,若坐标系内两个整点A(p,q),B(m,n)(m≤n)满足关于x的多项式
中,我们称横、纵坐标都是整数的点为整点,若坐标系内两个整点A(p,q),B(m,n)(m≤n)满足关于x的多项式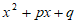 能够因式分解为(x+m)(x+n),则称点B是点A的分解点。例如A(3,2),B(1,2)满足
能够因式分解为(x+m)(x+n),则称点B是点A的分解点。例如A(3,2),B(1,2)满足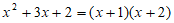 ,所以B是点A的分解点。
,所以B是点A的分解点。
(1)在点A1(-3,0),A2(5,6),A3(0,2)中,找出不存在分解点的是________;
(2)点P(a,1)存在分解点,求代数式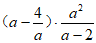 的值;
的值;
(3)点P,Q在纵轴上(P在Q的上方),点R在横轴上,且P,Q,R都存在分解点,若△PQR面积为9,请直接写出满足条件的点R的坐标:___________。
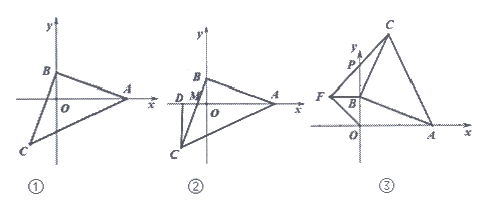
27. 如图,在三角形ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上。
(1)如图①,若点C的横坐标为-3,点B的坐标为__________;
(2)如图②,若x轴恰好平分∠BAC,BC交x轴于点M,过点C作CD垂直x轴于D点,试猜想线段CD与AM的数量关系,并说明理由;
(3)如图③,OB=BF,∠OBF=90°,连接CF交y轴于P点,点B在y轴的正半轴上运动时,△BPC与△AOB的面积比是否变化?若不变,直接写出其值。若变化,直接写出取值范围。
参考答案
一、选择题:本大题共10小题,每题3分,共30分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | B | C | A | A | D | C | A | B |
二、填空题:本大题共8小题,每题2分,共16分。
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
2 |
| -1 | 1 | 2 | HL | 45°或135° | 42 | 99 |
三、解答题:本大题共9小题,19题、20题每小题3分,21题、22题每题5分,23题~25题每题6分,26题、27题每题7分,共54分。
19. (1)原式=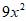 (2)原式=
(2)原式=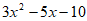
20. (1)
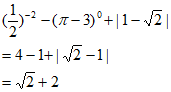
(2)
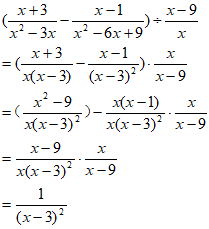
21. 解:
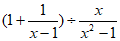
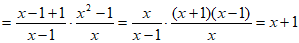 ,当
,当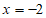 时,原式
时,原式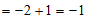
22. 解:两边同时乘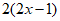 ,得
,得
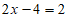 ,即
,即
x=3
经检验,x=3是原分式方程的解。
23.∵∠B=62°,AD⊥BC于D
∴∠BAD=28°
∵∠BAC=90°
∴∠DAC=62°
∵AE平分∠DAC,
∴∠DAE=31°
∴∠AEC=∠ADE+∠DAE=90°+31°=121°
24. 证明:∵BE=CF
∴BE+EC=CF+EC
∴BC=EF
在△ABC和△DEF中
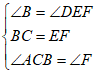
∴△ABC≌△DEF(ASA)
25. 解:设购买A型3M口罩的单价为x元,则B型口罩的单价为(x+3)元。
根据题意得: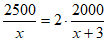
解得:x=5
经检验,x=5是原分式方程的解且符合题意。
答:该物业购买A型3M口罩的单价为5元。
26. (1)A3;
(2)由题意,得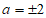 ,当
,当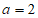 时,原式无意义,所以
时,原式无意义,所以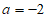 ,原式=
,原式=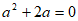
(3)(2,0)(-2,0)(6,0)(-6,0)
27. (1)(0,3)
(2)猜想:2CD=AM,理由如下:
延长CD,AB交于N,
∵x轴平分∠BAC
∴∠DAN=∠DAC
∵CD⊥x轴
∴∠NDA=∠CDA=90°
∵AD=AD
∴△AND≌△ADC(ASA)
∴DN=DC
∴CN=2CD
∵∠BAM+∠N=90°
∠BCN+∠N=90°
∴∠BAM=∠BCN
又∵∠ABM=∠CBN=90°
AB=BC
∴△ABM≌△CBN(ASA)
∴AM=CN=2CD
(3)不变,S△BPC:S△AOB=l:2