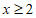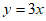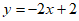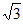一、选择题(本大题共10小题,每题4分,共40分)
1. 下列各式中,一定是最简二次根式的是(
)
A. 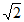 B.
B. 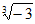 C.
C. 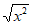 D.
D.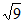
2. 如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是(
)
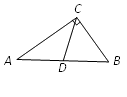
A. 20 B. 10 C. 5 D.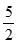
3. 下列线段能组成直角三角形的一组是(
)
A. 1,2,2 B. 3,4,5 C. 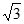 ,2,
,2,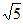 D. 5,6,7
D. 5,6,7
4. 如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是(
)
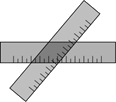
A. 矩形 B. 菱形 C. 正方形 D. 无法判断
5. 如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 2.5 | 2.5 | 6.4 | 7.1 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择(
)
A. 甲 B. 乙 C. 丙 D. 丁
6. 如图所示,函数 y = 2x 和 y = ax + 4 的图象相交于点A(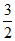 ,3),则关于 x 的不等式2x ≥ ax+4 的解集为( )
,3),则关于 x 的不等式2x ≥ ax+4 的解集为( )
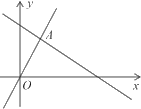
A. 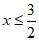 B.
B. 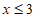 C.
C. 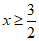 D.
D.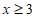
7. 如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各剪去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒。若纸盒的底面图中阴影部分)面积是32cm2,求剪去的小正方形的边长。设剪去的小正方形边长是xcm,根据题意可列方程为( )
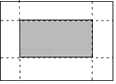
A. B.
C.( D.(
8. 在平面直角坐标系中,A、B、C三点的坐标分别为(0,0)、(0,-5)、(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在(
)
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
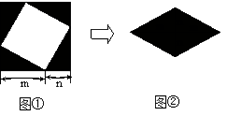
9. 图①是一个边长为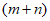 的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是(
的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是(
)
A. 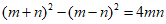
B. 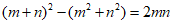
C. 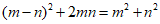
D. 
10. 小明、小聪参加了100 m跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图。
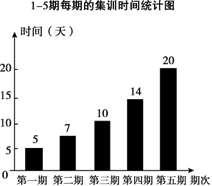
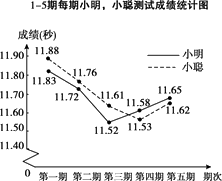
图1 图2
根据图中信息,有下面四个推断:
①这5期的集训共有56天;
②小明5次测试的平均成绩是11.68秒;
③从集训时间看,集训时间不是越多越好,集训时间过长,可能造成劳累,导致成绩下滑;
④从测试成绩看,两人的最好成绩都是在第4期出现,建议集训时间定为14天。
所有合理推断的序号是( )
A. ①③ B. ②④ C. ②③ D. ①④
二、填空题(本大题共10小题,每题3分,共30分)
11. 若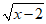 在实数范围内有意义,则实数x的取值范围是______。
在实数范围内有意义,则实数x的取值范围是______。
12. 已知是关于x的方程的一个根,则的值是____。
13. 若正比例函数图象经过点A(1,3),则该函数的解析式是________。
14. 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B两点间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A、B的点C,再找到AC,BC的中点D和E,并且测出DE的长为10m,则A、B间的距离为____m。
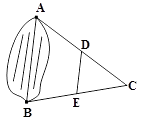
15. 已知点 A(5,y1)和点 B(4,y2)都在直线y = x + b 上,则y1与y2的大小关系为________。
16. 比较实数的大小: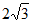 ____
____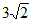 。
。
17. 一次函数y= −x+3的图象不经过第______象限。
18. 已知一次函数 y = kx + b的图象是由函数 y = −2x 的图象向上平移 2个单位得到的,则该一次函数的解析式为________。
19. 如图,在菱形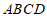 中,
中,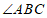 =120°,点E是边
=120°,点E是边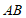 的中点,P是对角线
的中点,P是对角线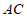 上的一个动点,若AB=2,则PB+PE的最小值是________。
上的一个动点,若AB=2,则PB+PE的最小值是________。
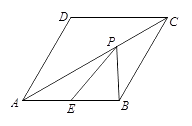
20. 在¨ ABCD中,对角线AC、BD相交于点O,E是边AB上的一个动点(不与A、B重合),连接EO 并延长,交 CD 于点 F,连接AF,CE,有下列四个结论:
①对于动点E,四边形AECF 始终是平行四边形;
②若∠ABC>90°,则至少存在一个点 E,使得四边形 AECF 是矩形;
③若 AB>AD ,则至少存在一个点 E,使得四边形 AECF 是菱形;
④若∠BAC = 45°,则至少存在一个点 E,使得四边形 AECF 是正方形。
以上所有错误说法的序号是____________。
三、解答题(共50分,第21~22题各5分,第23~26题各6分,第27~ 28题各8分)
21. 计算: 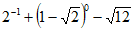 。
。
22. 解方程:。
23. 已知关于x的一元二次方程。
求证:无论m为何值,方程总有两个实数根;
若方程只有一个根为负数,求m的取值范围。
24. 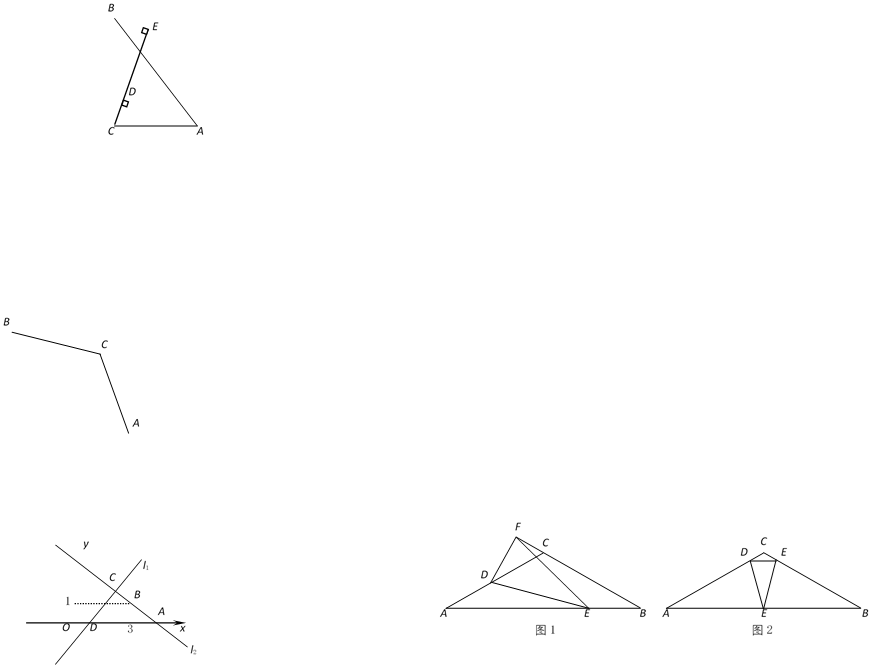 如图,在平面直角坐标系xOy中,直线AB与x轴交于点(2,0),与y轴交于点B(0,-4)。
如图,在平面直角坐标系xOy中,直线AB与x轴交于点(2,0),与y轴交于点B(0,-4)。
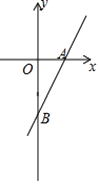
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且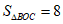 ,求点C的坐标。
,求点C的坐标。
25. 如图,在□ABCD中,点E,F分别在边BC,AD上,BE=DF,∠AEC=90°。
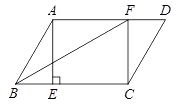
(1)求证:四边形AECF是矩形;
(2)连接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的长。
26. 2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗击疫情。为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传。某校为了了解初二年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试。现随机抽取甲、乙两班各15名同学的测试成绩(满分100分)进行整理分析,过程如下:
收集数据:
甲班15名学生测试成绩分别为:78,83,89,97,98,85,100,94,87,90,93,92,99,95,100。
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
整理数据:
班级 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x<100 |
甲 | 1 | 1 | 3 | 4 | 6 |
乙 | 1 | 2 | 3 | 5 | 4 |
分析数据:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 92 | a | 93 | 47.3 |
乙 | 90 | 87 | b | 50.2 |
应用数据:
(1)根据以上信息,可以求出:a=______分,b=________分;
(2)若规定测试成绩92分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可)。
27. 定义:若关于x的一元二次方程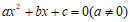 的两个实数根为
的两个实数根为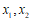 (
(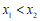 ),
),
分别以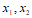 为横坐标和纵坐标得到点M
为横坐标和纵坐标得到点M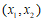 ,则称点M为该一元二次方程的衍生点。
,则称点M为该一元二次方程的衍生点。
(1)若方程为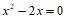 ,写出该方程的衍生点M的坐标。
,写出该方程的衍生点M的坐标。
(2)若关于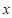 的一元二次方程
的一元二次方程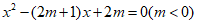 的衍生点为M,过点M向
的衍生点为M,过点M向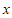 轴和
轴和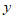 轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求
轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求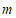 的值。
的值。
(3)是否存在b,c,使得不论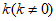 为何值,关于
为何值,关于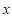 的方程
的方程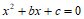 的衍生点M始终在直线
的衍生点M始终在直线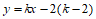 的图象上。若存在,直接写出b,c的值,若不存在,请说明理由。
的图象上。若存在,直接写出b,c的值,若不存在,请说明理由。
28. 如图,在正方形ABCD中,AB=6,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF。
(1)当DM=2时,依题意补全图1;
(2)在(1)的条件下,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,请直接写出此时DM与AD 的数量关系________________。
参考答案
一、选择题(本大题共10小题,每题4分,共40分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | C | B | B | A | C | D | D | B | A |
二、填空题(本大题共10小题,每题3分,共30分)
题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
答案 |
| -1 |
| 20 | 〉 | 〈 | 三 |
|
| ②④
|
三、解答题(共50分,第21~22题各5分,第23~26题各6分,第27~ 28题各8分)
21. 计算: 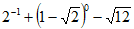 。 22. 解方程:。
。 22. 解方程:。
=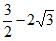
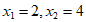
23. 证明:
(1)由于
,
方程总有两个实数根;
(2)解:由于,
或,
此方程有一个根是负数,
,
的取值范围是。
24.(1)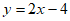 ;(2) C(4,4)
;(2) C(4,4)
25.(1)证明:∵□ABCD,
∴BC=AD,BC∥AD。
又∵BE=DF,
∴BC-BE=AD-DF,即EC=AF,
∴ECAF,
∴四边形AECF为平行四边形。
又∵∠AEC=90°,
∴四边形AECF是矩形。
(2)解法一:
在Rt△ABE中,∠AEB=90°,∠ABE=60°,AB=4,
∴BE=2,AE=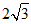 。
。
∵四边形AECF是矩形,
∴FC⊥BC,FC=AE=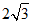 。
。
∵BF平分∠ABC,
∴∠FBC=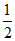 ∠ABC=30°,
∠ABC=30°,
在Rt△BCF中,∠FCB=90°,∠FBC=30°,FC=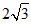 ,
,
∴BC=6,
∴AD=BC=6。
解法二:∵BF平分∠ABC,
∴∠ABF=∠FBC。
∵BC∥AD,
∴∠AFB=∠FBC,
∴∠AFB=∠ABF,
∴AF=AB=4。
在Rt△ABE中,∠AEB=90°,∠ABE=60°,AB=4,
∴BE=2,
∴FD=BE=2,
∴AD=AF+FD=6。
26.(1)100;91;(2)成绩为优秀的学生共有256人;(3)甲班的学生防疫测试的整体成绩较好。理由:平均分较高,中位数较大,方差小。
27. 解:(1)解得: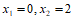
故方程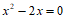 的衍生点为M
的衍生点为M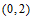
(2)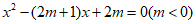
解得: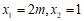
方程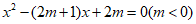 的衍生点为
的衍生点为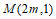
点M在第二象限内且纵坐标为1,由于过点M向两坐标轴作垂线,两条垂线与x轴、y轴恰好围城一个正方形,所以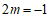 ,解得
,解得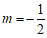
(3)存在。
直线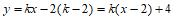 ,过定点
,过定点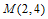 。
。
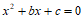 两个根为
两个根为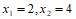
解得: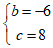
28. 解:(1)补全图形如图1所示。
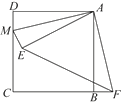
图1
(2)如图2,连接BM。
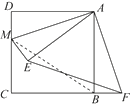
图2
∵点D与点E关于AM所在的直线对称,
∴AE=AD,∠MAD=∠MAE。
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°。
又∵DM = BF,
∴△ADM≌△ABF。
∴AF=AM,∠FAB=∠MAD。
∴∠FAB=∠MAE。
∴∠FAB+∠BAE=∠BAE+∠MAE。
∴∠FAE=∠MAB。
∴△FAE≌△MAB(SAS)。
∴EF=BM。
∵四边形ABCD是正方形,
∴BC=CD=AB=6。
∵DM=2,∴CM=4。∴在Rt△BCM中,BM=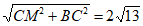
∴EF=2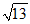 。
。
(3)当点M在CD边上运动时,若使△AEF为等腰三角形,则
AD=2DM或AD=DM