(本试卷满分100分,考试时间120分钟)
本试卷共25题,满分100分,考试时间120分钟。
一、选择题(本题共24分,每小题3分)
1. 民族图案是数学文化中的一块瑰宝。下列图案中,是轴对称图形但不是中心对称图形的是(
)



A B C D
2. 抛物线y=(x-2)2+1的顶点坐标是(
)
A. (2,1) B. (-2,1) C.(-2,-1) D.(1,2)
3. 下列各式中计算正确的是(
)
A. x2·x4=x6 B. 2m-(n+1)=2m-n+1
C. x5+2x5=3x10 D.(2a)3=2a3
4. A(– ,y1),B(1,y2),C(4,y3)三点都在二次函数y=–(x-2)2+k的图像上,则y1,y2,y3的大小关系为(
,y1),B(1,y2),C(4,y3)三点都在二次函数y=–(x-2)2+k的图像上,则y1,y2,y3的大小关系为(
)
A. y1<y2<y3 B. y1<y3<y2
C. y3<y1<y2 D. y3<y2<y1
5. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED∥AB,则∠1的度数为(
)
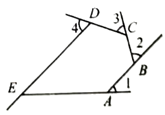
A. 55° B. 45° C. 35° D. 25°
6. 在平面直角坐标系xOy中,点A的坐标是(-2,0),点B的坐标是(0,6),将线段AB绕点B逆时针旋转90°后得到线段A’B。若反比例函数y=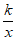 的图像恰好经过A’点,则k的值是(
的图像恰好经过A’点,则k的值是(
)
A. 9 B. 12 C. 15 D. 24
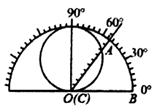
7. 某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转。从图中所示的图尺可读出sin∠AOB的值是(
)
A. 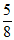 B.
B. 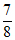 C.
C. 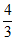 D.
D.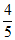
8. 为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某学校初二(8)班举办了“乐知杯古诗词“大赛。现有小璟、小桦、小花三位同学进入了最后冠军的角逐。决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军。下表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,下列说法正确的是(
)
第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 | 第六轮 | 最后得分 | |
小璟 | a | a | 26 | ||||
小桦 | a | b | c | 11 | |||
小花 | b | b | 11 |
A.
小璟可能有一轮比赛获得第二名 B. 小桦有三轮比赛获得第三名
C. 小花可能有一轮比赛获得第一名 D. 每轮比赛第一名得分a为5
二、填空题(本题共24分,每小题3分)
9. 已知关于x的不等式组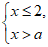 无解,则a的取值范围是_________。
无解,则a的取值范围是_________。
10. 圆心角是90°,半径为20的扇形的弧长为_________。
11. 某班学生分组做抛掷瓶盖实验,各组实验结果如下表:
累计抛掷次数 | 100 | 200 | 300 | 400 | 500 |
盖面朝上次数 | 54 | 105 | 158 | 212 | 264 |
盖面朝上的频率 | 0.5400 | 0.5250 | 0.5267 | 0.5300 | 0.5280 |
根据表中的信息,估计掷一枚这样的瓶盖,落地后盖面朝上的概率为________。(精确到0.01)
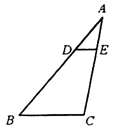
12. 如图,△ABC中,点D,E分别在AB,AC上,DE∥BC。若AD=1,BD=2,则△ADE与△ABC的面积之比为________。
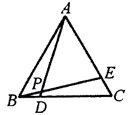
13. 如图,等边△ABC中,BD=CE,AD与BE相交于P,则∠APE的度数为________度。
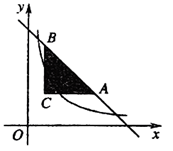
14. 如图,过点C(1,2)分别作x轴,y轴的平行线,交直线y=-x+6于A,B两点,若反比例函数y=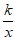 (x>0)的图像与△ABC有公共点,则k的取值范围是________。
(x>0)的图像与△ABC有公共点,则k的取值范围是________。
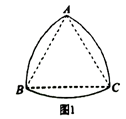
15. 中国科学技术馆有“圆与非圆“展品,涉及了“等宽曲线“的知识。因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线“。除了圆以外,还有一些几何图形也是“等宽曲线“,如勒洛三角形(图1),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形,图2是等宽的勒洛三角形和圆。
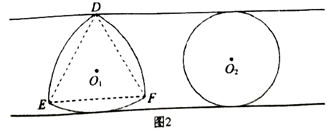
下列说法:
①勒洛三角形是轴对称图形;
②图1中,点A到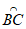 上任意一点的距离都相等;
上任意一点的距离都相等;
③图2中,勒洛三角形上任意一点到等边三角形DEF的中心O1的距离都相等;
④图2中,勒洛三角形的周长与圆的周长相等。其中说法正确的是________。
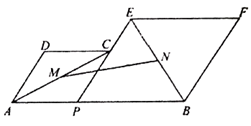
16. 如图,已知AB=12,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为________。
三、解答题(本题共52分,第17-20题,每小题5分,第21-23题,每小题6分,第24-25题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17.(本小题5分)
(1)计算(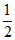 )
)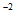 –(
–(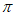 –
–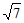 )0+|
)0+|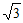 -2|+4cos30°;
-2|+4cos30°;
(2)如果a-2b=0,求代数式1-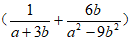 ÷
÷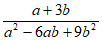 的值。
的值。
18. (本小题5分)
在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,连接OE并延长到点F,使EF=EO,连接AF,BF。
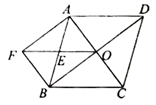
(1)求证:四边形AOBF是矩形;
(2)若AD=5,cos∠AFO=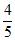 ,求菱形ABCD的面积。
,求菱形ABCD的面积。
19. (本小题5分)
在平面直角坐标系xOy中,双曲线y=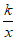 过点A(1,1),与直线y=4x交于B,C两点(点B的横坐标小于点C的横坐标)。
过点A(1,1),与直线y=4x交于B,C两点(点B的横坐标小于点C的横坐标)。
(1)求k的值;
(2)求点B,C的坐标;
(3)若直线x=t与双曲线y=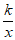 交于点D(t,y1),与直线y=4x交于点E(t,y2),当y1<y2时,直接写出t的取值范围。
交于点D(t,y1),与直线y=4x交于点E(t,y2),当y1<y2时,直接写出t的取值范围。
20. (本小题5分)
教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果。现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息。
a. 教育未来指数得分的频数分布直方图(数据分成7组:20≤x<30,30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x≤90);
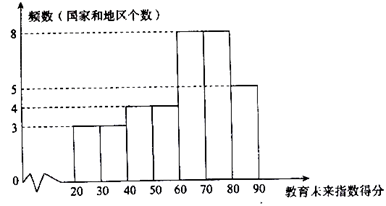
b. 未来教育指数得分在60≤x<70这一组的是:
61. 2 62. 8 64. 6 65. 2 67. 2 67. 3 67. 5 68. 5
c. 35个国家的人均国内生产总值和教育未来指数得分情况统计图
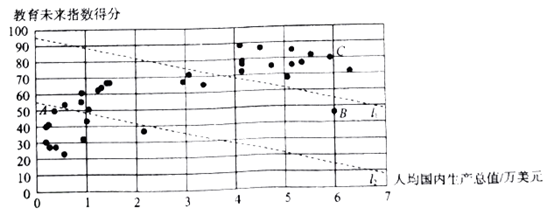
d. 中国内地和中国香港的未来教育指数得分分别为32. 9和68. 5。
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)中国香港的教育未来指数得分排名世界第________;
(2)在35个国家和地区的人均国内生产总值和国家教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○“画出代表中国香港的点;
(3)在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为________万美元;(结果保留一位小数)
(4)下列推断合理的是________。(填序号)
①相较于点A、C所代表的国家和地区,中国内地的教育未来指数得分还有一定差距,“十三五“规划提出“教育优先发展,教育强则国家强“的任务,进一步提高国家教育水平;
②相较于点B、C所代表的国家和地区,中国内地的人均国内生产总值还有一定差距,中国提出”决胜全面建成小康社会“的奋斗目标,进一步提高人均国内生产总值。
21. (本小题6分)
如图,△ABC中,AB=AC,以AC为直径的⊙O与BC相交于点D,与BA的延长线相交于点E,过点D作DF⊥AB交AB于点F。
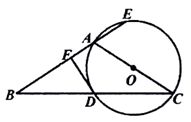
(1)求证:直线DF与⊙O相切;
(2)如果sinB=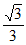 ,AE的长为2,求OA的长。
,AE的长为2,求OA的长。
22. (本小题6分)
甲同学想利用特殊角的三角函数值来计算75°角的三角函数值,他是这样思考的:
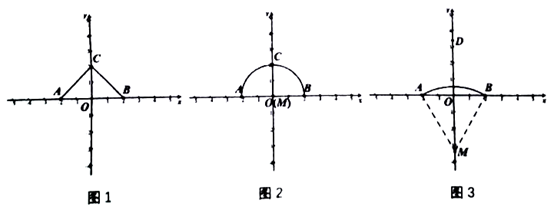
首先,因为45°+30°=75°,可以画出∠MON=45°,并在∠MON的外部再作∠NOP=30°,则∠MOP=75°(如图1)。
然后,在OP上取点A,设OA=1,作AB⊥OM于点B,则sin75°=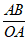 =AB,也就是说,只要求出AB的长度,就可以求出75°的正弦。
=AB,也就是说,只要求出AB的长度,就可以求出75°的正弦。
接着,作AC⊥ON于C,作CD⊥OM于D,作AE⊥CD交DC的延长线于点E(如图2),最后可以运用解直角三角形的知识和方法求出AB的长。
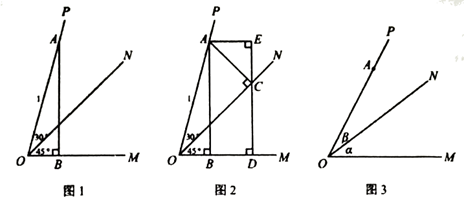
(1)根据甲同学的思路,补全下面的计算过程:
在Rt△AOC中,∠ACO=90°,∠AOC=30°,OA=1所以AC=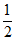 ,OC=
,OC=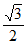 。
。
在Rt△COD中,∠CDO=90°,∠COD=45°,OC=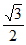 ,所以CD=_______。
,所以CD=_______。
在Rt△ACE中,∠E=90°,∠ACE=_______,AC=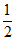 ,所以CE=_______。
,所以CE=_______。
可以证明四边形ABDE是矩形,所以AB=DE=_______,即sin75°=_______。
(2)借鉴甲同学的思路,乙同学提出了更进一步的问题:如图3,∠MON=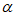 ,∠NOP=
,∠NOP=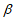 ,则∠MOP=
,则∠MOP=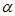 +
+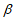 ,请构造图形,并用
,请构造图形,并用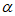 和
和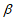 的三角函数来表示sin(
的三角函数来表示sin(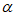 +
+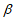 )=________。
)=________。
23. (本小题6分)
在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图像经过点A(0,-4)和B(-2,2)。
(1)求c的值,并用含a的式子表示b;
(2)当-2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,直接写出a的取值范围。
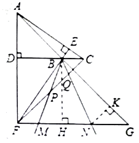
24. (本小题7分)
已知:△ABC的高AD所在直线与高BE所在直线相交于点F。
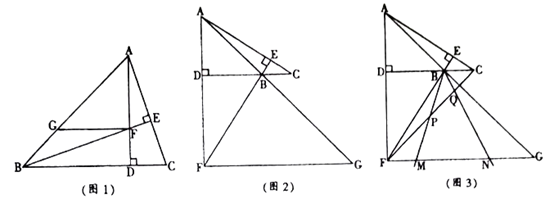
(1)如图1,若△ABC为锐角三角形,且∠ABC=45°,过点F作FG∥BC,交直线AB于点G,求证:FG+DC=AD;
(2)如图2,若∠ABC=135°,过点F作FG∥BC,交直线AB于点G,则FG,DC,AD之间满足的数量关系是_________。
(3)在(2)的条件下,若AG=5 ,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M,N两点(如图3),连接CF,线段CF分别与线段BM,线段BN相交于P,Q两点,若NG=
,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M,N两点(如图3),连接CF,线段CF分别与线段BM,线段BN相交于P,Q两点,若NG= ,求线段PQ的长。
,求线段PQ的长。
25. (本小题7分)
在平面直角坐标系xOy中,对于点P和图形W,如果以P为端点的任意一条射线与图形W最多只有一个公共点,那么称点P独立于图形W。
已知点A(-2,0),B(2,0),C(0,2)。
(1)如图1,作折线AC-CB。
①在点P1(0,3),P2(3,0),P3(2,4),P4(2,-1)中,独立于折线AC-CB的点是__________;
②点P是直线l:y=2x+4的一个动点,若点P独立于折线AC-CB,求点P的横坐标xP的取值范围;
(2)已知M(0,m),其中m≤0,以M为圆心,MA为半径作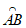 。
。
①如图2,若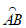 经过点C,请在图2中画出独立于
经过点C,请在图2中画出独立于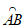 的所有点组成的图形(用阴影表示)。
的所有点组成的图形(用阴影表示)。
②如图3,∠AMB=60°,D(0,2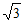 ),若以D为圆心,r为半径的⊙D上的所有点都独立于劣弧AB,请直接写出r的取值范围_________。
),若以D为圆心,r为半径的⊙D上的所有点都独立于劣弧AB,请直接写出r的取值范围_________。
参考答案
一、选择题(本题共24分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | A | B | B | D | D | D |
二、填空题(本题共24分,每小题3分)
9. a≥2 10. 10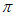
11. 0. 53 12. 1:9
13. 60 14. 2≤k≤9
15. ①②④ 16. 3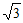
三、解答题(本题共52分,第17-20题,每小题5分,第21-23题,每小题6分,第24-25题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. (1)原式=4-1+2-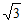 +2
+2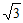 =5+
=5+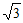 ;
;
(2)化简原式=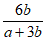 ,把a=2b代入得
,把a=2b代入得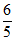 。
。
18. (1)因为点E为AB的中点,EF=EO,
所以四边形AOBF是平行四边形,
又因为四边形ABCD是菱形,
所以AC⊥BD,∠AOB=90°,
所以四边形AOBF是矩形。
(2)因为四边形AOBF是矩形,
所以AB=OF,∠FAO=90°,
又因为四边形ABCD是菱形,所以AB=AD=5,OF=5。
因为在Rt△AFO中,OF=5,cos∠AFO=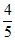 ,
,
所以AF=4,AO=3。
所以在菱形ABCD中,AC=6,BD=8。
所以菱形ABCD的面积=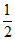 ×6×8=24。
×6×8=24。
19. (1)因为双曲线y=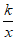 过点A(1,1),所以k=1。
过点A(1,1),所以k=1。
(2)由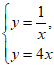 得
得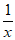 =4x,去分母,得4x2=1,解得x1=-
=4x,去分母,得4x2=1,解得x1=-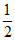 ,x2=
,x2=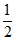 。
。
经检验,x1=–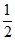 ,x2=
,x2=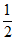 是原方程的解。
是原方程的解。
所以y1=-2,y2=2。
因为点B的横坐标小于点C的横坐标,所以B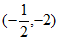 ,C
,C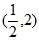 。
。
(3)当y1<y2时,–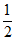 <t<0或t>
<t<0或t>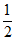 ,
,
20. (1)14;(2)如图所示;(3)6. 3;(4)①②
21. (1)连接OD。
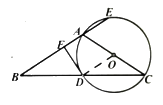
因为AB=AC,所以∠B=∠C。
因为OC=OD,所以∠C=∠ODC。
所以∠B=∠ODC。
因为OD∥AB,所以∠ODF=∠DFB。
因为DF⊥AB,∠DFB=90°。
所以∠ODF=90°,半径OD⊥DF。
DF是⊙O的切线。
(2)连接AD,CE,如图。
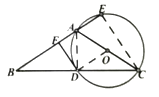
因为AC是⊙O的直径,
所以∠ADC=∠E=90°。
因为AB=AC,所以BD=CD。
因为∠DFB=∠E=90°,所以DF∥CE。
所以EF=BF。
设OA长为r,则AB=AC=2r。
因为AE=2,
所以EF=FB=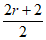 =r+1,所以AF=r-1。
=r+1,所以AF=r-1。
因为∠ADF+∠FDB=90°,∠FDB+∠B=90°。
所以∠B=∠ADF。
因为sinB=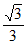 ,所以sinB=sin∠ADF=
,所以sinB=sin∠ADF=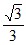 。
。
所以AD=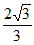 r,所以
r,所以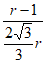 =
=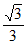 。
。
所以r=3即OA长为3。
22. (1)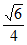 ,45°,
,45°,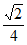 ,EC+CD=
,EC+CD=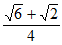 ;
;
(2)sin(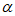 +
+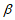 )=sin
)=sin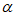 cos
cos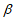 +cos
+cos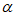 sin
sin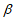 。
。
23. (1)c=-4,b=2a-3;
(2)当a<0时,需满足–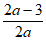 ≤-2,解得–
≤-2,解得–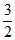 ≤a<0;
≤a<0;
当a>0时,需满足–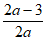 ≥0解得0<a≤
≥0解得0<a≤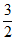 ;
;
所以a的取值范围是–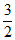 ≤a<0或0<a≤
≤a<0或0<a≤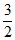 ;
;
(3)a的取值范围是0<a<4或a=-3-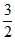
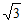
24. (1)因为∠ADB=90°,∠ABC=45°,
所以∠BAD=∠ABC=45°,所以AD=BD。
因为∠BEC=90°,所以∠CBE+∠C=90°,
因为∠DAC+∠C=90°,所以∠CBE=∠DAC。
因为GF∥BD,所以∠AGF=∠ABC=45°,
所以∠AGF=∠BAD,所以FA=FG,所以FG+DC=FA+DF=AD。
(2)FG-DC=AD。
(3)如图,因为∠ABC=135°,所以∠ABD=45°,
因为∠ADB=90°,所以∠DAB=∠DBA=45°,所以AD=BD,
因为FG∥BC,所以∠G=∠DBA=∠DAB,所以AF=FG。
所以AG=5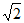 ,FG2+AF2=AG2,所以FG=AF=5。
,FG2+AF2=AG2,所以FG=AF=5。
因为DC=3,由(2)知FG-DC=AD,所以AD=BD=2,BC=1,DF=3,所以△FDC为等腰直角三角形。
所以FC=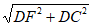 =3
=3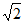 。
。
分别过B,N作BH⊥FG于点H,NK⊥BG于点K,所以四边形DFHB为矩形。
所以HF=BD=2,BH=DF=3,所以BH=HG=3,
所以BG=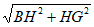 =3
=3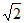 ,又因为sinG=
,又因为sinG=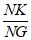 ,
,
所以NK=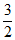 ×
×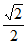 =
=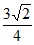 ,所以BK=
,所以BK=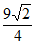 。
。
因为∠MBN=∠HBG=45°,所以∠MBH=∠NBK,因为∠MHB=∠NKB=90°,
所以△MBH~△NBK,所以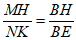 。
。
所以MH=1,FM=1。
因为BC∥FG,所以∠BCF=∠CFN,
因为∠BPC=∠MPF,CB=FM,
所以△BPC≌△MPF,所以PC=PF=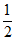 FC=
FC=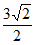 ,
,
因为∠BQC=∠NQF,所以△BCQ~△NFQ,
所以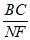 =
=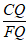 ,所以
,所以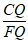 =
=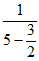 =
=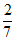 。
。
所以CQ=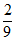 FC=
FC=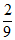 ×3
×3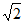 =
=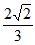 ,
,
所以PQ=CP-CQ=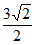 –
–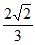 =
=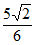 。
。
25. (1)①P1和P4;
②xP<-2或xP>–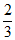 。
。
(2)①如图所示,不包含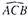 上的点;
上的点;
②0<r≤2。