(本试卷满分120分,考试时间100分钟)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知函数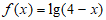 的定义域为M,函数
的定义域为M,函数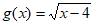 的定义域为N,则M
的定义域为N,则M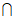 N=(
N=(
)
A. M B. N C. {4} D.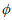
2. sin2021°可化简为(
)
A. sin41° B. -sin41° C. cos41° D. -cos41°
3. 向量“a,b不共线“是“| a+ b|<| a|+| b |“的(
)
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 函数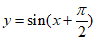 ,x∈(–
,x∈(–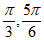 ]的值域为(
]的值域为(
)
A. [-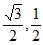 ) B. [-
) B. [-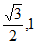 ] C. [-
] C. [-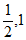 ] D. [-
] D. [-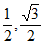 )
)
5. 已知偶函数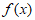 在(–
在(–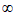 ,0)上单调递减,若a=f(1),b=f(2),c=f(–
,0)上单调递减,若a=f(1),b=f(2),c=f(–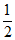 ),则a,b,c的大小关系为(
),则a,b,c的大小关系为(
)
A. a>b>c B. a>c>b C. b>a>c D. c>a>b
6. 甲、乙两人解关于x的方程:log2x+b+clogx2=0,甲写错了常数b,得到根为x=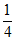 ,x=
,x=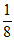 ;乙写错了常数c,得到根为x=
;乙写错了常数c,得到根为x=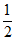 ,x=64。那么原方程的根正确的是(
,x=64。那么原方程的根正确的是(
)
A. x=4 B. x=3 C. x=4或x=8 D. x=2或x=3
7. 已知2cos2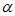 -3 sin2
-3 sin2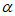 =1,
=1,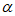 ∈(–
∈(–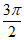 ,–
,–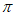 ),那么tan
),那么tan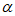 的值为(
的值为(
)
A. 2 B. -2 C. 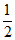 D. –
D. –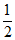
8. 如图所示的是函数y=sinx(0≤x≤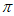 )的图像,A(x,y)是图像上任意一点,过点A作x轴的平行线,交图像于另一点B(A,B可重合)。设线段AB的长为f(x),则函数f(x)的图像是(
)的图像,A(x,y)是图像上任意一点,过点A作x轴的平行线,交图像于另一点B(A,B可重合)。设线段AB的长为f(x),则函数f(x)的图像是(
)
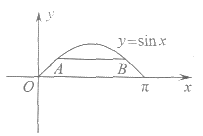
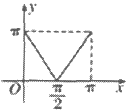
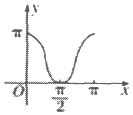
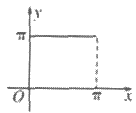
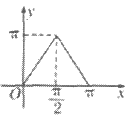
A B C D
9. 已知3 sin(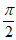 –
–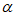 )-sin(
)-sin(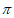 +
+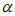 )=-
)=-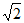 ,则cos
,则cos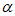 -sin
-sin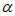 的取值可以为(
的取值可以为(
)
A. 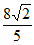 B.
B. 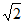 C. –
C. –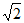 D. –
D. –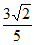
10. 如图,一个摩天轮的半径为10 m,轮子的最低处距离地面2m,如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点P(点P与摩天轮中心O的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17 m的时间大约是(
)
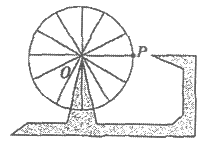
A. 8分钟 B. 10分钟 C. 12分钟 D. 14分钟
二、填空题共6小题,每小题5分,共30分。
11. 已知向量a=(1,-2),b=(x,4),且a∥b,则实数x=_______________。
12. 若角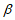 与角
与角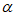 =
=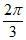 的终边关于直线y=x对称,则角
的终边关于直线y=x对称,则角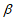 的终边上的所有角的集合可以写为___________。
的终边上的所有角的集合可以写为___________。
13. 已知幂函数f(x)=(m-1)2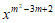 在(0,+
在(0,+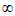 )上单调递增,则实数m的值为________。
)上单调递增,则实数m的值为________。
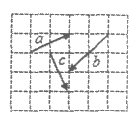
14. 在如图所示的方格纸中,向量a,b,c的起点和终点均在格点(小正方形顶点)上,若c与xa+yb(x,y为非零实数)共线,则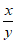 的值为_________。
的值为_________。
15. 某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常。排气4分钟后测得车库内一氧化碳浓度为64 ppm(ppm为浓度单似,1ppm表示百万分之一)。经检验知,该地下车库一氧化碳浓度y(ppm)与排气时间t(分钟)之间存在函数关系y=27-mt(m为常数)。求得m=________;若空气中一氧化碳浓度不高于0.5 ppm为正常,那么至少需要排气________分钟才能使这个地下车库中一氧化碳含量达到正常状态。
16. 已知△ABC,点P是平面上任意一点,且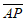 =
=
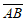 +
+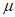
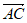 (
(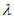 ,
,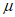 ∈R),给出以下命题:
∈R),给出以下命题:
①若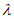 =
=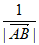 ,
,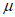 =
=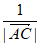 ,则P为△ABC的内心;
,则P为△ABC的内心;
②若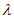 =
=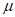 =1,则直线AP经过△ABC的重心;
=1,则直线AP经过△ABC的重心;
③若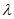 +
+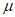 =1,且
=1,且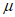 >0,则点P在线段BC上;
>0,则点P在线段BC上;
④若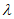 +
+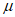 >1,则点P在△ABC外;
>1,则点P在△ABC外;
⑤若0<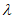 +
+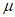 <1,则点P在△ABC内。
<1,则点P在△ABC内。
其中真命题为_________。
三、解答题共4小题,共50分。解答应写出文字说明、演算步骤或证明过程。
17. (本小题12分)
已知函数f(x)=1+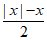 (-2<x≤2)。
(-2<x≤2)。
(1)求函数f(x)的值域;
(2)若函数g(x)=logax的图像与函数f(x)的图像有交点,请直接写出实数a的取值范围。
18.(本小题12分)
已知关于x的方程2x2–bx+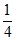 =0的两根为sin
=0的两根为sin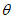 和cos
和cos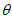 ,
,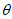 ∈(
∈(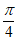 ,
,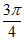 )。
)。
(1)求实数b的值;
(2)求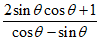 的值。
的值。
19.(本小题13分)
已知函数f(x)=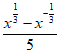 ,g(x)=
,g(x)= 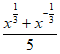 。
。
(1)①直接写出函数f(x)的奇偶性;
②写出函数f(x)的单调递增区间,并用定义证明;
(2)计算:f(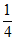 )-5 f(
)-5 f(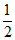 )g(
)g(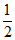 )=__________;
)=__________;
f(4)-5f(2)g(2)=___________;
f(9)-5f(3)g(3)=___________;
(3)由(2)中的各式概括出f(x)和g(x)对所有不等于0的实数x都成立的一个等式,并加以证明。
20. (本小题13分)
设A是由n个实数构成的一个有序数组,记作:A=(a1,a2,…,ai…,an)。其中ai(i=1,2,…,n)称为数组A的“元”,i称为数组A的“元”ai的下标。如果数组S=(b1,b2,…,bm)(m≤n,m∈N+)中的每个“元“都是来自数组A中不同下标的“元“。则称S为A的“子数组“。定义两个数组A=(a1,a2,…,an),B=(b1,b2,…,bn)的“关系数“为C(A,B)= a1 b1+ a2 b2+…+ anbn。
(1)若A=(–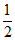 ,
,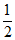 ),B=(b1,b2, b3,b4),且B中的任意两个“元“互不相等,B的含有两个”元“的不同“子数组“共有p个,分别记为S1,S2,…,Sp。
),B=(b1,b2, b3,b4),且B中的任意两个“元“互不相等,B的含有两个”元“的不同“子数组“共有p个,分别记为S1,S2,…,Sp。
①p=________;
②若bj∈N+,1≤bj≤101(j=1,2,3,4),记X=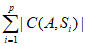 ,求X的最大值与最小值;
,求X的最大值与最小值;
(2)若A=(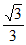 ,
,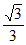 ,
,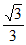 ),B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元“的“子数组“,求C(A,S)的最大值。
),B=(0,a,b,c),且a2+b2+c2=1,S为B的含有三个“元“的“子数组“,求C(A,S)的最大值。
参考答案
1. D 2. B 3. A 4. B 5. C 6. C 7. D 8. A 9. C 10. B
11. -2 12. {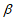 |
|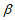 =-
=-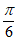 +2k
+2k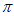 ,k∈Z} 13. 0
,k∈Z} 13. 0
14. 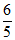 15.
15. 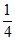 ;32 16. ②④
;32 16. ②④
17. (1)当0≤x≤2时,f(x)=1+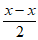 =1;
=1;
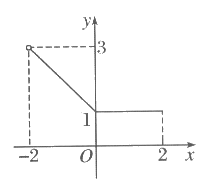
当-2<x<0时,f(x)=1+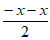 =1-x。
=1-x。
所以f(x)=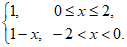
函数的值域为[1,3)。
(2)实数a的取值范围是(0,1) (1,2]。
(1,2]。
18. (1)因为sin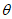 ,cos
,cos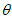 为关于x的方程
为关于x的方程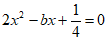 的两根,
的两根,
所以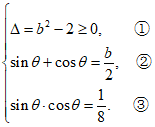
由②③,得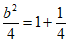 ,解得b=±
,解得b=±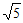 ,此时△=5-2>0,
,此时△=5-2>0,
又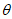 ∈(
∈(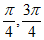 ),所以sin
),所以sin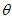 +cos
+cos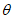 >0,所以b=
>0,所以b=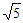 。
。
(2)由(1),得sin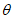 +cos
+cos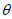 =
=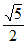 ,又
,又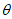 ∈(
∈(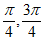 ),所以sin
),所以sin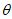 >cos
>cos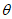 ,
,
所以cos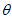 -sin
-sin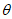 =
=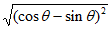 =
=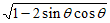 =-
=-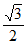 ,
,
所以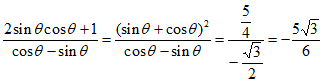 。
。
19. (1)①因为函数f(x)的定义域是(–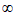 ,0)
,0)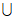 (0,+
(0,+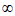 ),所以定义域关于原点对称。
),所以定义域关于原点对称。
又因为f(–x)=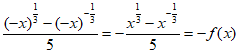 ,
,
所以函数f(x)是奇函数。
②函数f(x)的单调递增区间为(–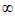 ,0),(0,+
,0),(0,+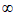 )。
)。
证明:在(0,+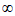 )上任取x1,x2,且x1< x2,
)上任取x1,x2,且x1< x2,
则(x1)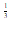 <( x2)
<( x2)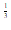 ,(x2)
,(x2)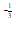 <( x1)
<( x1)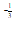 ,从而
,从而
f(x1)–f(x2)=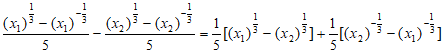 <0,
<0,
即f(x1)<f(x2),所以f(x)=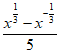 在(0,+∞)上单调递增。
在(0,+∞)上单调递增。
又因为f(x)是奇函数,所以f(x)在(-∞,0)上也单调递增。
所以函数f(x)的单调递增区间为(-∞,0),(0,+∞)。
(2)0,0,0.
(3)由(2)推测出一个等式:f(x2)-5f(x)g(x)=0(x≠0)。
证明如下:f(x2)-5f(x)g(x)
=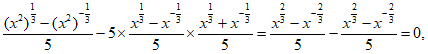
所以f(x2)-5f(x)g(x)=0(x≠0)成立。
20. (1)①12。
②X=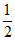 (|b1– b2|+| b1– b3|+| b1– b4|+| b2– b1|+| b2– b3|+| b2– b4|
(|b1– b2|+| b1– b3|+| b1– b4|+| b2– b1|+| b2– b3|+| b2– b4|
+| b3– b1|+| b3– b2|+| b3– b4|+| b4– b1|+| b4– b2|+| b4– b3|)
=| b1– b2|+| b1– b3|+| b1– b4|+| b2– b3|+| b2– b4|+| b3– b4|。
因为B中的任意两个“元“互不相等,不妨设b1< b2< b3< b4,则X=3 b4+ b3– b2-3 b1。
又1≤b3– b2≤98,3≤b4– b1≤100,所以10≤X≤398。
当b1=l,b2=2,b3=100,b4=101时,X取最大值398。
当b1=l,b2=2,b3=3,b4=4时,X取最小值10。
(2)①当0是S中的“元“时,根据B中a,b,c三个“元“的对称性,
可只求解C(A,S)=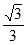 (a+b)的最大值,其中a2+b2+c2=1。
(a+b)的最大值,其中a2+b2+c2=1。
因为(a+b)2=a2+b2+2ab≤2(a2+b2)≤2(a2+b2+c2)=2,
所以–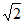 ≤a+b≤
≤a+b≤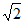 。
。
当且仅当a=b=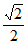 ,c=0时,a+b达到最大值
,c=0时,a+b达到最大值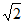 ,
,
从而C(A,S)max=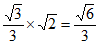 。
。
②当0不是S中的“元”时,即求解C(A,S)=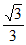 (a+b+c)的最大值,
(a+b+c)的最大值,
其中a2+b2+c2=1。
因为(a+b+c) 2=a2+b2+c2+2ab+2ac+2bc≤3(a2+b2+c2)=3,
所以当且仅当a=b=c=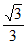 时,a+b+c取得最大值
时,a+b+c取得最大值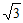 ,
,
此时C(A,S)max=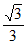 (a+b+c)=1。
(a+b+c)=1。
综上,C(A,S)的最大值为1。
