本试卷共150分。考试时长120分钟。
第一部分
(选择题
共50分)
一、选择题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 在复平面内,复数z对应的点的坐标是(2,1),则复数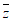 =
=
A. 2-i B. 1-2i C. 2+i D. 1+2i
2. 在(a+b)n的展开式中,只有第4项的二项式系数最大,则n=
A. 4 B. 5 C. 6 D. 7
3. 椭圆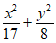 =1的焦点坐标为
=1的焦点坐标为
A. (5,0),(-5,0) B. (3,0),(-3,0)
C. (0,5),(0,-5) D. (0,3),(0,-3)
4. 已知直线l1:ax-y-1=0,l2:ax+(a+2)y+1=0。若l1⊥l2,则实数a=
A. -1或1 B. 0或1
C. -1或2 D. -3或2
5)已知平面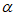 ⊥平面
⊥平面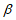 ,
,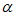
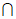
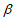 =l。下列结论中正确的是
=l。下列结论中正确的是
A. 若直线m⊥平面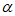 ,则m∥
,则m∥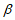
B. 若平面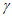 ⊥平面
⊥平面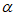 ,则
,则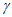 ∥
∥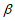
C. 若直线m⊥直线l,则m⊥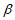
D. 若平面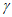 ⊥直线l,则
⊥直线l,则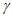 ⊥
⊥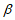
6. 将4张座位编号分别为1,2,3,4的电影票全部分给3人,每人至少1张。如果分给同一人的2张电影票具有连续的编号,那么不同的分法种数是
A. 24 B. 18 C. 12 D. 6
7. 已知双曲线C: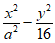 =1的两个焦点是F1,F2,点P在双曲线C上。若C的离心率为
=1的两个焦点是F1,F2,点P在双曲线C上。若C的离心率为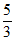 ,且|PF1|=10,则|PF2|=
,且|PF1|=10,则|PF2|=
A. 4或16 B. 7或13
C. 7或16 D. 4或13
8. 在正三棱锥P-ABC中,AB=3,PA=2,则直线PA与平面ABC所成角的大小为
A. 30° B. 45° C. 60° D. 75°
9. 已知圆O1的方程为(x-a)2+(y-b)2=4,圆O2的方程为x2+(y-b+1)2=1,其中a,b∈R。那么这两个圆的位置关系不可能为
A. 外离 B. 外切 C. 内含 D. 内切
10. 点M在直线l:x=2上,若椭圆C:x2+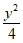 =1上存在两点A,B,使得△MAB是等腰三角形,则称椭圆C具有性质P。下列结论中正确的是
=1上存在两点A,B,使得△MAB是等腰三角形,则称椭圆C具有性质P。下列结论中正确的是
A. 对于直线l上的所有点,椭圆C都不具有性质P
B. 直线l上仅有有限个点,使椭圆C具有性质P
C. 直线l上有无穷多个点(但不是所有的点),使椭圆C具有性质P
D. 对于直线l上的所有点,椭圆C都具有性质P
第二部分
(非选择题
共100分)
二、填空题共6小题,每小题4分,共24分。
11. 已知复数z=i·(1+i),则|z|=_______。
12. 若双曲线C:x2–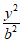 =l(b>0)的焦距为2
=l(b>0)的焦距为2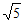 ,则b=_______;C的渐近线方程为_______。
,则b=_______;C的渐近线方程为_______。
13. 设(x-2)4=a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4=_______。
14. 在空间直角坐标系Oxyz中,已知点A(1,0,0),B(0,2,0),C(0,0,2),D(0,0,1),则直线AD与BC所成角的大小是_______。
15. 已知抛物线y2=4x的焦点为F,准线为l,点P在抛物线上,PQ⊥l于点Q。若△PQF是锐角三角形,则点P的横坐标的取值范围是_______。
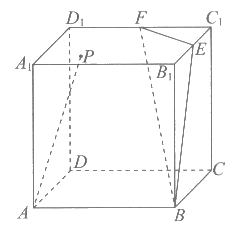
16. 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为B1C1,C1D1的中点,P是底面A1B1C1D1上一点。若AP∥平面BEF,则AP长度的最小值是_______;最大值是_______。
三、解答题共6小题,共76分。解答应写出文字说明,演算步骤或证明过程。
17. (本小题10分)
生物兴趣小组有12名学生,其中正、副组长各1名,组员10名。现从该小组选派3名同学参加生物学科知识竞赛。
(I)如果正、副组长2人中有且只有1人入选,共有多少种不同的选派方法?
(II)如果正、副组长2人中至少有1人入选,且组员甲没有入选,共有多少种不同的选派方法?
18. (本小题12分)
已知圆C过原点O和点A(1,3),圆心在直线y=1上。
(I)求圆C的方程;
(II)直线l经过点O,且l被圆C截得的弦长为2,求直线l的方程。
19. (本小题13分)
如图,在正三棱柱ABC-A1B1C1中,AB=AA1,D,E,F分别是BC,BB1,AA1的中点。
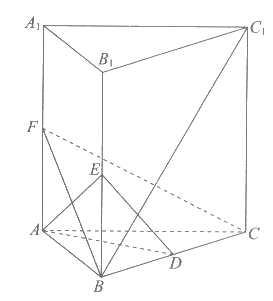
(I)求证:CF∥平面ADE:
(II)求证:BC1⊥平面ADE。
20. (本小题13分)
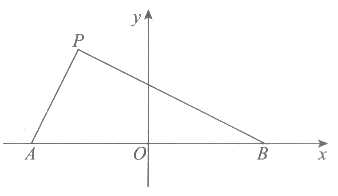
如图,设点A,B在x轴上,且关于原点O对称。点P满足tan∠PAB=2,tan∠PBA=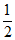 ,且△PAB的面积为20。
,且△PAB的面积为20。
(I)求点P的坐标;
(II)以A,B为焦点,且过点P的椭圆记为C。设M(x0,y0)是C上一点,且-1<x0<3,求y0的取值范围。
21. (本小题14分)
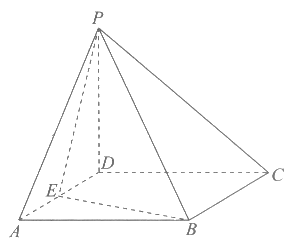
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,E为AD的中点,底面ABCD是边长为2的正方形,且二面角P-BE-C的余弦值为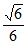 。
。
(I)求PD的长;
(II)求点C到平面PEB的距离。
22. (本小题14分)
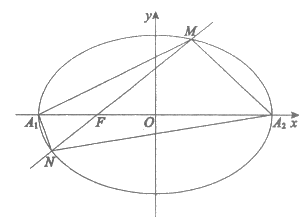
已知椭圆C: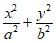 =1(a>b>0)的一个焦点为F(-l,0),A1(-a,0),A2(a,0),且|A2F|=3。
=1(a>b>0)的一个焦点为F(-l,0),A1(-a,0),A2(a,0),且|A2F|=3。
(I)求椭圆C的方程;
(II)过点F的直线交椭圆C于点M,N。记△A1MN和△A2MN的面积分别为S1和S2。
当S2-S1=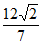 时,求直线MN的方程。
时,求直线MN的方程。
参考答案
一、选择题(共10小题,每小题5分,共50分)
1. A 2. C 3. B 4. C 5. D
6. B 7. A 8. A 9. C 10. D
二、填空题(共6小题,每小题4分,共24分)
11. 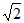 12. 2 y=±2x
12. 2 y=±2x
13. -15 14. 60°
15. (1,+∞) 16.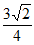
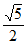
注:12、16题每空2分。
三、解答题(共6小题,共76分)
17. (共10分)
解:(I)正、副组长2人中有且只有1人入选,
选派方法数为C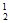 ·C
·C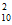 =90。 ……3分
=90。 ……3分
(II)正、副组长2人都入选,且组员甲没有入选,
选派方法数为C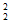 C
C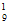 =9。 ……6分
=9。 ……6分
正、副组长2人中有且只有1人入选,且组员甲没有入选,选派方法数为
C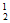 C
C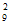 =72。 …9分
=72。 …9分
所以正、副组长2人中至少有1人入选,且组员甲没有入选,选派方法数为
9+72=81。 ……10分
18. (共12分)
解:(I)设圆C的圆心坐标为(a,1)。 ……1分
依题意,有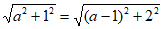 , ……3分
, ……3分
解得a=2。 ……4分
从而圆C的半径为r=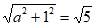 , ……5分
, ……5分
所以圆C的方程为(x-2)2+(y-1)2=5。 ……6分
(II)依题意,圆C的圆心到直线l的距离为2。 ……7分
显然直线x=0符合题意。 ……8分
当直线l的斜率存在时,设其方程为y=kx,即kx-y=0。 ……9分
所以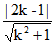 =2, …10分
=2, …10分
解得k=-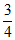 。 ……11分
。 ……11分
所以直线l的方程为y=-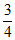 x。 ……12分
x。 ……12分
综上,直线l的方程为x=0或3x+4y=0。
19. (共13分)
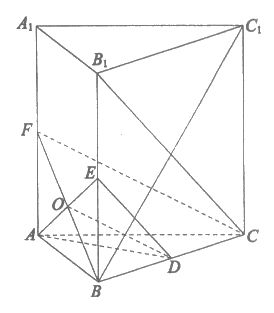
解:(I)设AE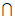 BF=O,连接OD。
BF=O,连接OD。
因为ABC-A1B1C1为正三棱柱,且AB=AA1,
所以侧面A1ABB1为正方形。 ……1分
因为E,F分别是BB1,AA1的中点,
所以O是BF的中点。 ……2分
又因为D是BC的中点,
所以OD∥CF。 ……4分
因为OD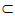 平面ADE,CF
平面ADE,CF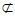 平面ADE, ……5分
平面ADE, ……5分
所以CF∥平面ADE。 ……6分
(II)因为△ABC为正三角形,
所以AD⊥BC。 ……7分
又CC1⊥平面ABC,
所以AD⊥CC1。 ……8分
所以AD⊥平面B1BCC1。 ……9分
所以BC1⊥AD。 ……10分
连接B1C。
因为侧面B1BCC1为正方形,
所以BC1⊥B1C。 ……11分
所以BC1⊥DE。 ……12分
所以BC1⊥平面ADE。 ……1 3分
20. (共13分)
解:(I)设A(-c,0),B(c,0)。
则直线PA的方程为y=2(x+c),直线PB的方程为y=- (x-c)。 ……2分
(x-c)。 ……2分
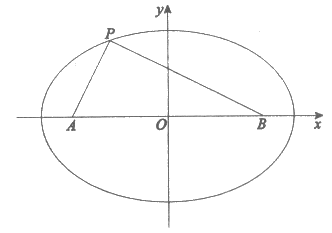
由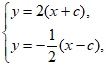 解得
解得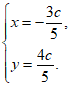
所以P(–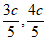 ). …3分
). …3分
故△PAB的面积S=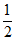 |AB|·|yP|=
|AB|·|yP|=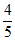 c2。 ……4分
c2。 ……4分
所以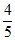 c2=20,
c2=20,
解得c=5。 ……5分
所以点P的坐标为(-3,4)。 ……6分
(II)由(I)得A(-5,0),B(5,0),
所以|PA|=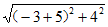 =2
=2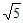 ,|PB|=
,|PB|=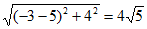 。……8分
。……8分
设以A,B为焦点且过点P的椭圆方程为C: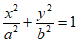 。
。
则a=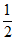 (|PA|+|PB|)=3
(|PA|+|PB|)=3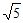 ,又b2=a2-c2=20, ……10分
,又b2=a2-c2=20, ……10分
所以椭圆C的方程为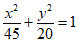 . ……11分
. ……11分
所以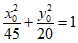 ,即
,即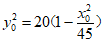 。
。
因为-1<x0<3,所以0≤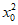 <9。
<9。
所以16<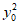 ≤20。 ……12分
≤20。 ……12分
所以y0的取值范围是[-2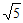 ,-4)
,-4) (4,2
(4,2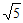 ]。 ……13分
]。 ……13分
21. (共14分)
解:(I)依题意,DA,DC,DP两两互相垂直,如图
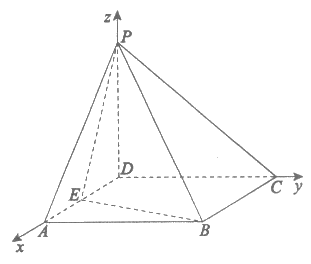
建立空间直角坐标系D-xyz。 ……1分
设PD=h(h>0)。
由题意得E(1,0,0),B(2,2,0),P(0,0,h)。
所以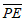 =(1,0,-h),
=(1,0,-h),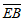 =(1,2,0)。
=(1,2,0)。
设平面PEB的法向量为n=(x0,y0,z0),
则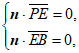 即
即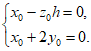 …4分
…4分
令x0=2,则y0=-1,z0=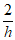 。
。
于是n=(2,-l,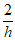 )。 ……6分
)。 ……6分
又因为PD⊥平面ABCD,
所以平面ABCD的一个法向量为m=(0,0,1)。 ……7分
依题意,有cos<m,n>=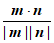 =
=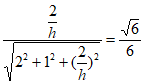 , …。9分
, …。9分
解得h=2,
所以PD=2。 ……10分
(II)由(I)得,平面PEB的法向量为n=(2,-1,1)。 ……11分
又C(0,2,0),
所以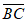 =(-2,0,0)。 ……12分
=(-2,0,0)。 ……12分
所以点C到平面PEB的距离为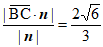 。 …。14分
。 …。14分
22. (共14分)
解:(I)依题意,椭圆C的半焦距c=1, ……1分
所以|A2F|=a+c=3。
解得a=2。 ……2分
所以b2=a2-c2=3。 ……3分
所以椭圆C的方程为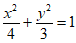 。 ……4分
。 ……4分
(II)当直线MN的斜率不存在时,其方程为x=-1。
此时M(-l,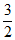 ),N(-1,–
),N(-1,–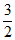 ),或M(-l,–
),或M(-l,–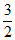 ),N(-l,
),N(-l,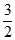 )。
)。
所以S1=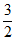 ,S2=
,S2=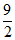 ,即S2-S1=3,不合题意。 ……5分
,即S2-S1=3,不合题意。 ……5分
当直线MN的斜率存在时,设其方程为y=k(x+1)(k≠0)。
由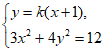 得(3+4k2)x2+8k2x+4k2-12=0。 …6分
得(3+4k2)x2+8k2x+4k2-12=0。 …6分
设M(x1,y1),N(x2,y2),则x1+x2=-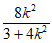 ,x1x2=
,x1x2=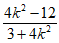 ……8分
……8分
因为S1=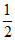 |A1F|(|y1|+|y2|),:S2=
|A1F|(|y1|+|y2|),:S2=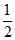 |A2F|(|y1|+|y2|),
|A2F|(|y1|+|y2|),
所以S2-S1=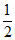 ×2×(|y1|+|y2|)=|y1-y2|=|k(x1-x2)| …10分
×2×(|y1|+|y2|)=|y1-y2|=|k(x1-x2)| …10分
=|k|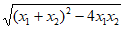
=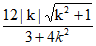 . …。12分
. …。12分
令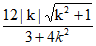 =
=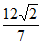 ,解得k=±1。 ……13分
,解得k=±1。 ……13分
所以直线MN的方程为x-y+1=0,或x+y+1=0。 ……14分
