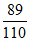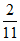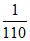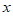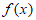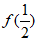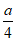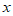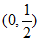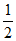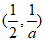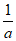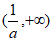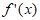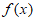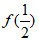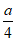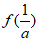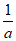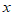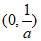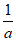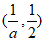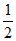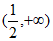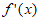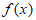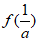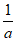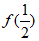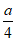(考试时间120分钟
满分150分)
本试卷分为选择题
(共40分)和非选择题
(共110分)两部分
第一部分
(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知全集U={-1,0,1,2,3,4},集合A={0,1,2},则 =
=
A. {3,4} B. {-1,3,4}
C. {0,1,2} D. {-1,4}
2. 已知向量a=(-1,2),b=(x,4),且a⊥b,则|b|=
A. 2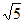 B. 4
B. 4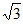 C. 4
C. 4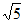 D. 8
D. 8
3. 某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,则该三棱锥的体积为
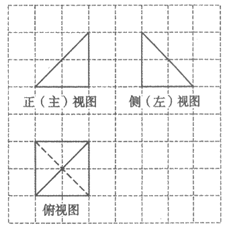
A. 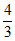 B.
B. 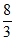 C. 3 D. 4
C. 3 D. 4
4. 已知等比数列{an}的各项均为正数,且a3=9,则log3a1+log3a2+ log3a3+ log3a4+ log3a5=
A. 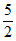 B.
B. 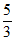 C. 10 D. 15
C. 10 D. 15
5. 设抛物线C:y2=4x的焦点为F,准线l与x轴的交点为M,P是C上一点。若|PF|=4,则|PM|=
A. 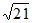 B. 5 C. 2
B. 5 C. 2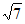 D. 4
D. 4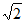
6. 已知函数f(x)=cos(2x-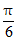 ),给出下列四个结论:
),给出下列四个结论:
①函数f(x)是周期为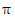 的偶函数;
的偶函数;
②函数f(x)在区间[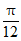 ,
,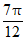 ]上单调递减;
]上单调递减;
③函数f(x)在区间[0,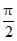 ]上的最小值为-1;
]上的最小值为-1;
④将函数f(x)的图象向右平移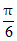 个单位长度后,所得图象与g(x)=sin2x的图象重合。
个单位长度后,所得图象与g(x)=sin2x的图象重合。
其中,所有正确结论的序号是
A. ①③ B. ②③ C. ①④ D. ②④
7. 已知定义在R上的奇函数f(x)满足f(x+2)=f(x),且f(1)=0,当x∈(0,1)时,f(x)=2x+x。设a=f(5),b=f(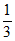 ),c=f(–
),c=f(–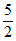 ),则a,b,c的大小关系为
),则a,b,c的大小关系为
A. b>a>c B. a>c>b C. c>a>b D. b>c>a
8. 已知圆C:x2+y2=4,直线l:x+y+t=0,则“l与C相交“是“|t|<2”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 已知双曲线C: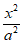 –
–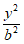 =1(a>0,b>0)的左焦点为F,右顶点为A,过F作C的一条渐近线的垂线FD,D为垂足。若|DF|=|DA|,则C的离心率为
=1(a>0,b>0)的左焦点为F,右顶点为A,过F作C的一条渐近线的垂线FD,D为垂足。若|DF|=|DA|,则C的离心率为
A. 2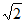 B. 2 C.
B. 2 C. 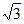 D.
D.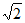
10. 在平面直角坐标系xOy中,已知直线y=mx(m>0)与曲线y=x3从左至右依次交于A,B,C三点。若直线l:kx-y+3=0(k∈R)上存在点P满足|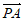 +
+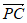 |=2,则实数k的取值范围是
|=2,则实数k的取值范围是
A. (-2,2) B. [-2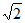 ,2
,2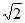 ]
]
C. (-∞,-2)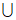 (2,+∞) D. (-∞,-2
(2,+∞) D. (-∞,-2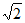 ]
]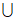 [2
[2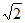 ,+∞)
,+∞)
第二部分
(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
11. 设a∈R。若复数z=i(1+ai)为纯虚数,则a=_______,z2=_______。
12. 在(x2+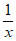 )6的展开式中,常数项是________。(用数字作答)
)6的展开式中,常数项是________。(用数字作答)
13. 在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦。根据《周髀算经》记载,西周数学家商高就发现勾股定理的一个特例:若勾为三,股为四,则弦为五。一般地,像(3,4,5)这样能够成为一个直角三角形三条边长的正整数组称为勾股数组。若从(3,4,5),(5,12,13),(6,8,10),(7,24,25),(8,15,17),(9,12,15),(9,40,41),(10,24,26),(11,60,61),(12,16,20)这些勾股数组中随机抽取1组,则被抽出的勾股数组中的三个数恰好构成等差数列的概率为________。
14. 若函数f(x)=sin(x+φ)+cosx为偶函数,则常数φ的一个取值为________。
15. 设函数y=f(x)的定义域为D,若对任意x1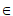 D,存在x2∈D,使得f(x1)·f(x2)=1,则称函数f(x)具有性质M,给出下列四个结论:
D,存在x2∈D,使得f(x1)·f(x2)=1,则称函数f(x)具有性质M,给出下列四个结论:
①函数y=x3-x不具有性质M;
②函数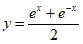 具有性质M;
具有性质M;
③若函数y=log8(x+2),x∈[0,t]具有性质M,则t=510;
④若函数y=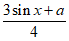 具有性质M,则a=5。
具有性质M,则a=5。
其中,正确结论的序号是________。
注:本题给出的结论中,有多个符合题目要求。全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
在△ABC中,cosA=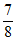 ,c=3,且b≠c,再从条件①、条件②中选择一个作为已知,求:
,c=3,且b≠c,再从条件①、条件②中选择一个作为已知,求:
(I)b的值;
(II)△ABC的面积。
条件①:sinB=2sinA:
条件②:sinA+sinB=2sinC。
注:如果选择条件①和条件②分别解答,按第一个解答计分。
17. (本小题13分)
某公司为了解用户对其产品的满意程度,从A地区随机抽取了400名用户,从B地区随机抽取了100名用户,请用户根据满意程度对该公司产品评分。该公司将收集到的数据按照[20,40),[40,60),[60,80),[80,100]分组,绘制成评分频率分布直方图如下:
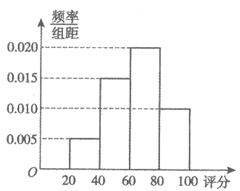
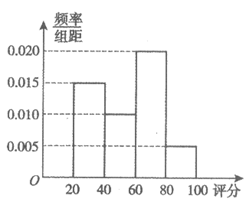
A地区用户满意程度评分频率分布直方图 B地区用户满意程度评分频率分布直方图
(I)从A地区抽取的400名用户中随机选取一名,求这名用户对该公司产品的评分不低于60分的概率;
(Ⅱ)从B地区抽取的100名用户中随机选取两名,记这两名用户的评分不低于80分的个数为X。求X的分布列和数学期望;
(Ⅲ)根据频率分布直方图,假设同组中的每个数据用该组区间的中点值代替,估计A地区抽取的400名用户对该公司产品的评分的平均值为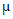 1,B地区抽取的100名用户对该公司产品的评分的平均值为
1,B地区抽取的100名用户对该公司产品的评分的平均值为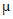 2,以及A,B两个地区抽取的500名用户对该公司产品的评分的平均值为
2,以及A,B两个地区抽取的500名用户对该公司产品的评分的平均值为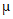 0,试比较
0,试比较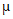 0和
0和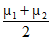 的大小。(结论不要求证明)
的大小。(结论不要求证明)
18. (本小题14分)
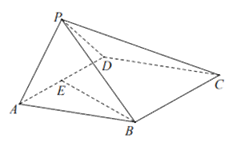
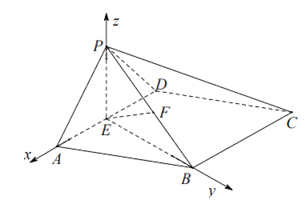
如图,在四棱锥P-ABCD中,底面ABCD为菱形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,∠BAD=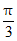 ,E是线段AD的中点,连结BE。
,E是线段AD的中点,连结BE。
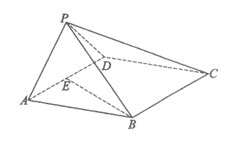
(I)求证:BE⊥PA;
(II)求二面角A-PD-C的余弦值;
(Ⅲ)在线段PB上是否存在点F,使得EF∥平面PCD?
若存在,求出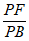 的值;若不存在,说明理由。
的值;若不存在,说明理由。
19. (本小题15分)
已知椭圆C: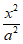 +
+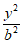 =1(a>b>0)过点(1,
=1(a>b>0)过点(1,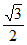 ),且C的离心率为
),且C的离心率为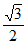 。
。
(I)求椭圆C的方程;
(Ⅱ)过点P(1,0)的直线l交椭圆C于A,B两点,求|PA|·|PB|的取值范围。
20. (本小题15分)
已知函数f(x)=lnx-(a+2)x+ax2(a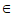 R)。
R)。
(I)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)若f(x)恰有两个零点,求实数a的取值范围。
21. (本小题15分)
已知无穷数列{an}满足:a1=0,an+1=a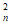 +c(n∈N*,c∈R)。对任意正整数n≥2,记Mn={c|对任意i∈{1,2,3,…,n},|ai|≤2},M={c|对任意i∈N*,|ai|≤2}。
+c(n∈N*,c∈R)。对任意正整数n≥2,记Mn={c|对任意i∈{1,2,3,…,n},|ai|≤2},M={c|对任意i∈N*,|ai|≤2}。
(I)写出M2,M3;
(II)当c>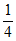 时,求证:数列{an}是递增数列,且存在正整数k,使得c
时,求证:数列{an}是递增数列,且存在正整数k,使得c Mk;
Mk;
(III)求集合M。
参考答案
一、选择题(共10小题,每小题4分,共40分)
1. B 2. C 3. A 4. C 5. C
6. D 7. A 8. B 9. B 10. D
二、填空题(共5小题,每小题5分,共25分)
11. 0;-1 12. 15
13. 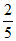 14.
14. 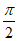 (答案不唯一)
(答案不唯一)
15. ①③
三、解答题(共6小题,共85分)
16. (共13分)
解:选条件①:sinB=2sinA。
(I)在△ABC中,因为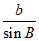 =
=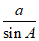 ,所以b=
,所以b=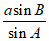 =2a。
=2a。
因为cosA=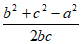 ,且c=3,cosA=
,且c=3,cosA=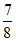 ,b=2a,
,b=2a,
所以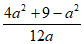 =
=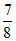 。
。
化简得2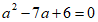 ,
,
解得a=2或a=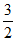 。
。
当a=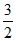 时,
时,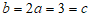 ,与题意矛盾。
,与题意矛盾。
所以a=2,所以b=4。 9分
(II)因为cosA=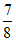 ,A∈(0,
,A∈(0,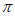 ),所以sinA=
),所以sinA=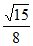 。
。
所以S△ABC=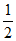 bcsinA=
bcsinA=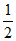 ×4×3×
×4×3×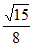 =
=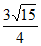 13分
13分
选条件②:sinA+sinB=2sinC。
(I)在△ABC中,因为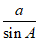 =
=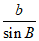 =
=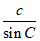 ,
,
所以由sinA+sinB=2sinC得a+b=2c=6。
因为cosA=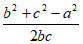 ,且c=3,cosA=
,且c=3,cosA=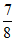 ,a=6-b,
,a=6-b,
所以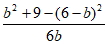 =
=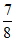 。
。
解得b=4。 9分
(II)由(I)知b=4,所以a=6-b=2。
因为cosA=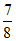 ,A∈(0,
,A∈(0,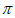 ),所以sinA=
),所以sinA=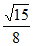 。
。
所以S△ABC=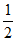 bcsinA=
bcsinA=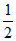 ×4×3×
×4×3×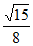 =
=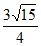 。 13分
。 13分
17. (共13分)
解:(I)由题知A地区共抽取400名用户,其中有240名用户对该公司产品的评分不低于60分,所以从A地区抽取的400名用户中随机选取一名,
这名用户对该公司产品的评分不低于60分的概率是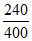 =0.6。 3分
=0.6。 3分
(II)由题可知X的可能取值为0,1,2。
P(X=0)=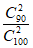 =
=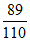 ;
;
P(X=1)=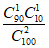 =
=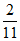 ;
;
P(X=2)=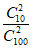 =
=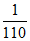 。
。
所以X的分布列如下表:
X | 0 | 1 | 2 |
P |
|
|
|
所以X的数学期望EX=0×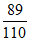 +1×
+1×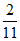 +2×
+2×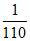 =
=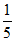 。 10分
。 10分
(III)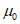 >
>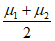 。 13分
。 13分
18. (共14分)
解:(I)因为四边形ABCD为菱形,所以AB=AD。
又因为∠BAD=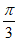 ,E为AD的中点,所以BE⊥AD。
,E为AD的中点,所以BE⊥AD。
又因为平面PAD⊥平面ABCD,
平面PAD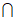 平面ABCD=AD,
平面ABCD=AD,
所以BE⊥平面PAD。
因为PA 平面PAD,
平面PAD,
所以BE⊥PA。 4分
(II)连结PE。因为PA=PD,E为AD的中点,
所以PE⊥AD。
由(I)可知BE⊥平面PAD,
所以BE⊥AD,PE⊥BE。
设AD=2a,则PE=a。
如图,建立空间直角坐标系E-xyz。
所以A(a,0,0),B(0, a,0),C(-2a,
a,0),C(-2a,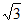 a,0),D(–a,0,0),P(0,0,a)。
a,0),D(–a,0,0),P(0,0,a)。
所以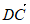 =(–a,
=(–a,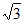 a,0),
a,0),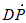 =(a,0,a)。
=(a,0,a)。
因为BE⊥平面PAD,所以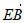 =(0,
=(0,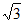 a,0)是平面PAD的一个法向量。
a,0)是平面PAD的一个法向量。
设平面PCD的法向量为n=(x,y,z),
则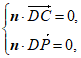 即
即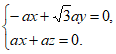 所以
所以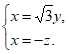
令x=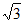 ,则y=1,z=
,则y=1,z=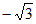 。于是n=(
。于是n=(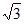 ,1,
,1,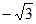 )。
)。
所以cos<n,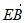 >=
>=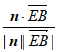 =
=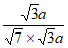 =
=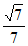 。
。
由题知,二面角A-PD-C为钝角,所以其余弦值为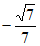 。 9分
。 9分
(III)当点F是线段PB的中点时,EF∥平面PCD。理由如下:
因为点E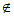 平面PCD,所以在线段PB上存在点F使得EF∥平面PCD等价于
平面PCD,所以在线段PB上存在点F使得EF∥平面PCD等价于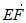 ·n=0。
·n=0。
假设线段PB上存在点F使得EF∥平面PCD。
设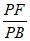 =
=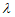 (
(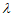 ∈[0,1]),则
∈[0,1]),则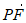 =
=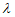
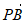 。
。
所以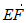 =
=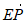 +
+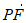 =
=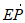 +
+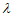
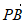 =(0,0,a)+
=(0,0,a)+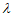 (0,
(0,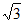 a,–a)=(0,
a,–a)=(0,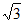
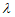 a,a–
a,a–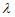 a)。
a)。
由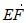 .n=
.n=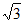
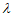 a-
a-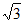 (a–
(a–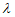 a)=0,得
a)=0,得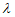 =
=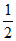 。
。
所以当点F是线段PB的中点时,EF∥平面PCD,且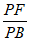 =
=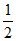 。 14分
。 14分
19. (共15分)
解:(I)由题意得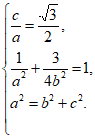 解得
解得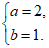
所以椭圆C的方程为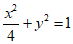 。 5分
。 5分
(II)当直线l的斜率不存在时,直线l:x=1与椭圆C交于A(1,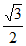 ),B(1,–
),B(1,–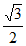 )两点,
)两点,
所以|PA|=|PB|=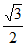 ,所以|PA|·|PB|=
,所以|PA|·|PB|=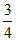 。
。
当直线l的斜率存在时,设其方程为y=k(x-1),
由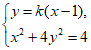 得
得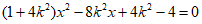 。
。
且△=64k4-4(1+4k2)(4k2-4)=16(3k2+1)>0。
设A(x1,y1),B(x2,y2),则
x1+x2=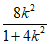 ,x1x2=
,x1x2=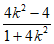 。
。
所以
|PA|·|PB|=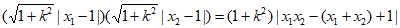
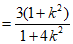
令t=1+4k2,则t≥1,
所以|PA|·|PB|=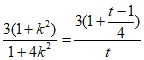 =
=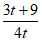 =
=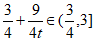 。
。
当t=1,即k=0时,|PA|·|PB|取最大值3。
综上所述,|PA|·|PB|的取值范围是[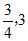 ]。 15分
]。 15分
20. (共15分)
解:(I)当a=0时,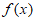 =lnx-2x,
=lnx-2x,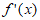 =
=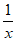 -2,
-2,
所以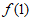 =-2,
=-2,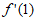 )=-1。
)=-1。
所以曲线在点(1,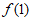 )处的切线方程为y+2=-(x-1),即x+y+1=0。 3分
)处的切线方程为y+2=-(x-1),即x+y+1=0。 3分
(II)因为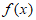 =lnx-(a+2)x+ax2,定义域为(0,+∞),
=lnx-(a+2)x+ax2,定义域为(0,+∞),
所以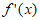 =
=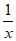 –(a+2)+2ax=
–(a+2)+2ax=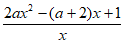 =
=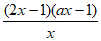 。
。
①当a≤0时, 与
与 在(0,+∞)上的变化情况如下:
在(0,+∞)上的变化情况如下:
|
|
|
|
| + | 0 | – |
| ↗ | 最大值 | ↘ |
所以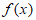 在(0,
在(0,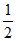 )内单调递增,在(
)内单调递增,在(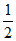 ,+∞)内单调递减。
,+∞)内单调递减。
②当0<a<2时,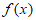 与
与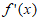 在(0,+∞)上的变化情况如下:
在(0,+∞)上的变化情况如下:
|
|
|
|
|
|
| + | 0 | – | 0 | + |
| ↗ | 极大值
| ↘ | 极小值
| ↗ |
所以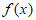 在(0,
在(0,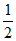 ),(
),(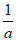 ,+∞)内单调递增,在(
,+∞)内单调递增,在(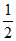 ,
,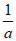 )内单调递减。
)内单调递减。
③当a=2时,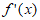 ≥0,所以
≥0,所以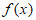 在(0,+∞)上单调递增。
在(0,+∞)上单调递增。
④当a>2时,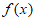 与
与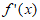 在(0,+∞)上的变化情况如下:
在(0,+∞)上的变化情况如下:
|
|
|
|
|
|
| + | 0 | – | 0 | + |
| ↗ | 极大值
| ↘ | 极小值
| ↗ |
所以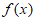 在(0,
在(0,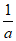 ),(
),(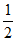 ,+∞)内单调递增,在
,+∞)内单调递增,在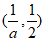 内单调递减。 9分
内单调递减。 9分
(III)由(II)可知:
①当a≤0时,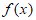 在(0,
在(0,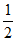 )内单调递增,在(
)内单调递增,在(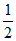 ,+∞)内单调递减,
,+∞)内单调递减,
当x=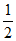 时,
时,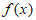 取得最大值
取得最大值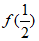 =-ln2-1-
=-ln2-1-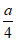 。
。
(i)当-4ln2-4≤a≤0时,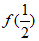 ≤0,
≤0,
所以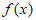 在(0,+∞)上至多有一个零点,不符合题意。
在(0,+∞)上至多有一个零点,不符合题意。
(ii)当a<-41n2-4时,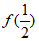 >0。
>0。
因为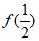 >0,
>0,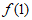 =-2<0,
=-2<0,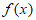 在(
在(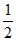 ,+∞)内单调递减,
,+∞)内单调递减,
所以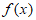 在(
在(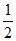 ,+∞)内有唯一零点。
,+∞)内有唯一零点。
因为a<-41n2-4<-e,
所以-a>e且0<-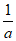 <
<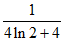 <
<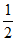 。
。
因为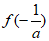 =-ln(-a)+1+
=-ln(-a)+1+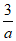 <1-1n(-a)<1-lne=0,
<1-1n(-a)<1-lne=0,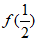 >0,
>0,
且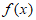 在(0,
在(0,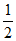 )内单调递增,所以
)内单调递增,所以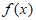 在(0,
在(0,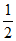 )内有唯一零点。
)内有唯一零点。
所以当a<-4ln2-4时,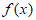 恰有两个零点。
恰有两个零点。
②当0<a<2时,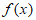 在(0,
在(0,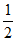 ),(
),(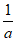 ,+∞)内单调递增,在(
,+∞)内单调递增,在(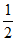 ,
,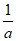 )内单调递减,
)内单调递减,
因为当x=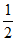 时,
时,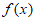 取得极大值
取得极大值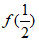 =-ln2-1-
=-ln2-1-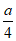 <0,
<0,
所以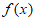 在(0,+∞)上至多有一个零点,不符合题意。
在(0,+∞)上至多有一个零点,不符合题意。
③当a=2时,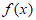 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
所以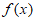 在(0,+∞)上至多有一个零点,不符合题意。
在(0,+∞)上至多有一个零点,不符合题意。
④当a>2时,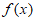 在(0,
在(0,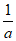 ),(
),(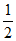 ,+∞)内单调递增,在(
,+∞)内单调递增,在(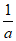 ,
,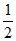 )内单调递减。
)内单调递减。
因为当x=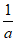 时,
时,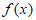 取得极大值
取得极大值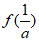 =-lna-1-
=-lna-1-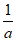 <0,
<0,
所以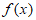 在(0,+∞)上至多有一个零点,不符合题意。
在(0,+∞)上至多有一个零点,不符合题意。
综上所述,实数a的取值范围是(–∞,-4ln2-4)。 15分
21. (共15分)
解:(I)M2=[-2,2],M3=[-2,1]。 4分
(Ⅱ)当c> 时,对任意n∈N*,都有
时,对任意n∈N*,都有
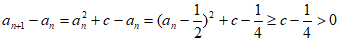 ,
,
所以an+1>an。
所以数列{an}是递增数列。 7分
因为
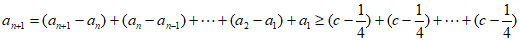 ,
,
所以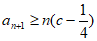 。
。
令n0=min{t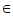 N|t>
N|t>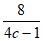 },则
},则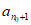
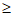 n0(c-
n0(c-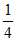 )>
)>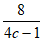 (c-
(c-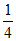 )=2,
)=2,
所以c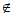
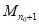 。
。
所以存在正整数k=n0+1,使得c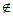 Mk。 9分
Mk。 9分
(III)由题意得,对任意n∈N*,都有Mn+1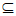 Mn且M
Mn且M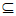 Mn。
Mn。
由(Ⅱ)可得,当c>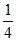 时,存在正整数k,使得c
时,存在正整数k,使得c Mk,所以c
Mk,所以c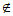 M。
M。
所以若c∈M,则c≤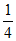 。
。
又因为M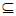 M3=[-2,1],所以若c∈M,则c≥-2。
M3=[-2,1],所以若c∈M,则c≥-2。
所以若c∈M,则-2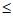 c
c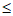
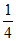 ,即M
,即M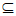 [-2,
[-2,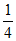 ]。
]。
下面证明[-2,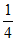 ]
] M。
M。
①当0≤c≤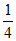 时,对任意n∈N*,都有an≥0。
时,对任意n∈N*,都有an≥0。
下证对任意n∈N*,an<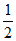 。
。
假设存在正整数k,使得ak≥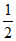 。
。
令集合S={k∈N*|ak≥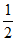 },则非空集合S存在最小数s0。
},则非空集合S存在最小数s0。
因为0≤a2=c≤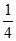 <
<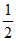 ,所以s0>2。
,所以s0>2。
因为s0-1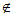 S,所以0≤
S,所以0≤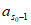 <
<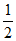 。
。
所以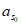 =
=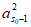 +c<
+c<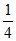 +c≤
+c≤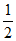 ,与
,与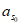 ≥
≥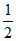 矛盾。
矛盾。
所以对任意n∈N*,0≤an<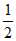 。
。
所以当0≤c≤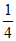 时,|an|≤2。
时,|an|≤2。
②当-2≤c<0时,c2+2c≤0。
下证对任意n∈N*,|an|≤|c|。
假设存在正整数k,使得|ak|>|c|。
令集合T={k∈N*||ak|>|c|},则非空集合T存在最小数t0。
因为a2=c,所以|a2|≤|c|,所以t0>2。
因为t0-1 T,所以|
T,所以|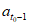 |≤|c|。
|≤|c|。
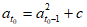 ≤
≤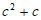 ≤-c,且
≤-c,且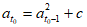 ≥c,
≥c,
所以|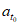 |≤|c|,与|
|≤|c|,与|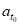 |>|c|矛盾。
|>|c|矛盾。
所以当-2≤c<0时,|an|≤|c|≤2。
所以当c∈[-2,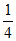 ]时,对任意n∈N*,都有|an|≤2。
]时,对任意n∈N*,都有|an|≤2。
所以c∈M,即[-2,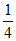 ]
]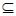 M。
M。
因为M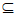 [-2,
[-2,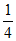 ],且[-2,
],且[-2,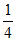 ]
]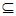 M,所以M=[-2,
M,所以M=[-2,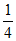 ]。 15分
]。 15分