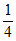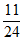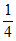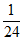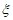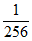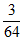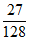(本试卷满分120分,考试时间100分钟)
一、选择题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 将2封不同的信投入3个不同的信箱,不同的投法种数为(
)
A. A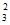 B. C
B. C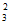 C. 32 D. 23
C. 32 D. 23
2. 已知盒子中装有3个红球,2个白球,5个黑球,它们的大小形状完全相同,现需一个红球,甲每次从中任取一个球,且不放回,则在甲第一次拿到白球的条件下,第二次拿到红球的概率为(
)
A. 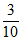 B.
B. 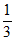 C.
C. 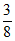 D.
D.
3. 若直线2x-y-4=0在x轴和y轴上的截距分别为a和b,则a-b的值为(
)
A. 6 B. 2 C. -2 D. -6
4. 若直线y=kx+1与圆x2+y2=1相交于P,Q两点,且∠POQ=90°(其中O为原点),则k的值为(
)
A. 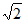 B. 1 C. ±
B. 1 C. ±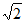 D. ±1
D. ±1
5. 将标号为1,2,3,4,5的五个小球放入三个不同的盒子中,每个盒子至少放一个小球,则不同的放法种数为(
)
A. 150 B. 300 C. 60 D. 90
6. (x3–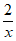 )4+(x+
)4+(x+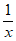 )8的展开式中的常数项为(
)8的展开式中的常数项为(
)
A. 32 B. 34 C. 36 D. 38
7. 过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=(
)
A. 2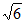 B. 8 C. 4
B. 8 C. 4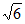 D. 10
D. 10
8. 双曲线C: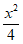 –
–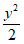 =1的右焦点为F,点P在C的一条渐近线上,O为坐标原点,则下列说法错误的是(
=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点,则下列说法错误的是(
)
A. 该双曲线离心率为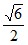
B. 双曲线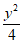 –
–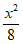 =1与双曲线C的渐近线相同
=1与双曲线C的渐近线相同
C. 若PO⊥PF,则△PFO的面积为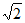
D. |PF|的最小值为2
9. 某市新高考方案规定的选课要求为:学生先从物理、历史两科中任选一科,再从化学、生物、政治、地理四科中任选两科,现有甲、乙两名学生按规定选科,则甲、乙恰有一门学科相同的选科方法种数为(
)
A. 24 B. 30 C. 48 D. 60
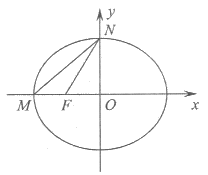
10. 已知椭圆C: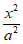 +
+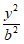 =1(a>b>0),点M,N,F分别为椭圆C的左顶点、上顶点、左焦点,若∠MFN=∠NMF+90°,则椭圆C的离心率是(
=1(a>b>0),点M,N,F分别为椭圆C的左顶点、上顶点、左焦点,若∠MFN=∠NMF+90°,则椭圆C的离心率是(
)
A. 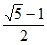 B.
B. 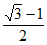 C.
C. 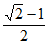 D.
D.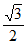
二、填空题共5小题,每小题5分,共25分。
11. 如果椭圆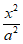 +
+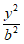 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为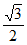 ,那么双曲线
,那么双曲线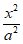 –
–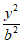 =1(a>0,b>0)的离心率为___________。
=1(a>0,b>0)的离心率为___________。
12. 已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2距离之和的最小值是___________。
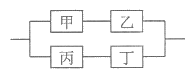
13. 如图所示,已知一个系统由甲、乙、丙、丁4个部件组成,当甲、乙都正常工作,或丙、丁都正常工作时,系统就能正常工作。若每个部件的可靠性均为r(0<r<1),而且甲、乙、丙、丁互不影响,则系统的可靠度为___________。
14. 甲、乙两人对同一目标各射击一次,甲命中的概率为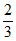 ,乙命中的概率为
,乙命中的概率为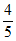 ,且他们的结果互不影响,若命中目标的人数为
,且他们的结果互不影响,若命中目标的人数为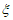 ,则E(
,则E(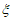 )=___________。
)=___________。
15. 已知点A(2,4)在抛物线y2=2px(p>0)上,直线l交抛物线于B,C两点,且直线AB与AC都是圆N:x2+y2-4x+3=0的切线,则B,C两点纵坐标之和是________,直线l的方程为___________。
三、解答题共5小题,共45分。解答应写出文字说明、演算步骤或证明过程。
16. (本小题10分)
从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为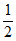 ,
,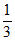 ,
,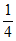 。
。
(1)记X表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;
(2)若有2辆车独立从甲地到乙地,求这2辆车共遇到1个红灯的概率。
17. (本小题10分)
已知椭圆C: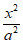 +
+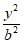 =1(a>b>0),过点(0,-1),离心率e=
=1(a>b>0),过点(0,-1),离心率e=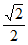 。
。
(1)求椭圆的标准方程;
(2)过右焦点F的直线l与椭圆C交于A,B两点,点M的坐标为(2,0),设直线AM和BM的斜率分别为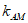 和
和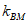 ,求
,求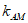 +
+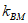 的值。
的值。
18. (本小题10分)
某不透明纸箱中共有4个小球,其中1个白球,3个红球,它们除了颜色外均相同。
(1)一次从纸箱中摸出两个小球,求恰好摸出2个红球的概率;
(2)每次从纸箱中摸出一个小球,记录颜色后放回纸箱,这样摸取4次,记取到红球的次数为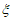 ,求
,求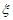 的分布列;
的分布列;
(3)每次从纸箱中摸出一个小球,记录颜色后放回纸箱,这样摸取20次,取到几次红球的概率最大?(只需写出结论)
19. (本小题10分)
设椭圆C: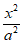 +
+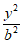 =1(a>b>0),F1,F2为左、右焦点,B为何轴端点,长轴长为4,焦距为2c,且b>c,△BF1F2的面积为
=1(a>b>0),F1,F2为左、右焦点,B为何轴端点,长轴长为4,焦距为2c,且b>c,△BF1F2的面积为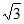 。
。
(1)求椭圆C的方程;
(2)设动直线l:y=kx+m与椭圆有且只有一个公共点M,且与直线x=4相交于点N,试探究:在坐标平面内是否存在定点P,使得以MN为直径的圆恒过定点P?若存在,求出点P的坐标;若不存在,请说明理由。
20. (本小题5分)
(1)设i为虚数单位,则(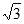 -i)7的实部为_________;
-i)7的实部为_________;
(2)计算: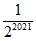 (1-3C
(1-3C +32C
+32C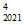 -33C
-33C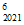 +…-31009C
+…-31009C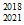 +31010C
+31010C )=_________。
)=_________。
参考答案
1. C
2. B
3. A
4. D
5. A
6. D
7. (2015高考课标II理7)C
可得圆的方程为x2+y2-2x+4y-20=0,令x=0,得y2+4y-20=0,设两个根为y1,y2,则y1+y2=-4,y1y2=-20,所以|MN|=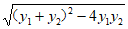 =4
=4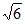 。
。
8. D
9. D
10. A
11. 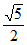 。
。
12. 2。
13. 2r2-r4。
14. 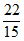 。
。
15. -8;15x+15y+22=0。
16. (2017高考天津理16)
(1)随机变量X的所有可能取值为0,1,2,3;
则P(X=0)=(1-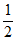 )×(1-
)×(1-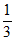 )×(1-
)×(1-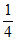 )=
)=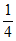 ,
,
P(X=1)=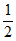 ×(1-
×(1-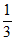 )×(1-
)×(1-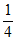 )+(1-
)+(1-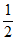 )×
)×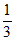 ×(1-
×(1-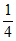 )+(1-
)+(1-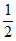 )×(1-
)×(1-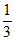 )×
)×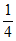 =
=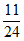 ,
,
P(X=2)=(1-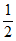 )×
)×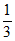 ×
×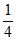 +
+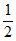 ×(1-
×(1-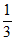 )×
)×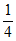 +
+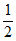 ×
×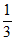 ×(1-
×(1-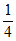 )=
)=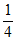 ,
,
P(X=3)=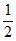 ×
×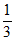 ×
×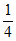 =
=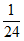 。
。
所以,随机变量X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
随机变量X的数学期望为E(X)=0×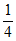 +1×
+1×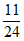 +2×
+2×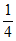 +3×
+3×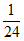 =
=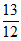 。
。
(2)设Y表示第一辆车遇到红灯的个数,Z表示第二辆车遇到红灯的个数,
则所求事件的概率为
P(Y+Z=1)=P(Y=0,Z=1)+P(Y=1,Z=0)
=P(Y=0)·P(Z=1)+P(Y=1)·P(Z=0)=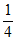 ×
×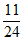 +
+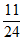 ×
×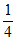 =
=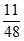 。
。
所以,这2辆车共遇到1个红灯的概率为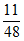 。
。
17. (1)依题意可得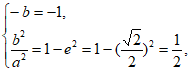 所以
所以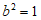 ,
,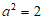 ,
,
所以椭圆的标准方程为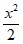 +
+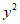 =1。
=1。
(2)因为F(1,0),直线l的斜率不为0,
所以设直线l的方程为x=my+1,A(x1,y1),B(x2.y2)。
由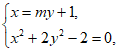 得
得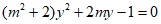 。
。
所以△=4m2+4(m2+2)=8>0,y1+y2=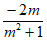 ,y1y2=
,y1y2=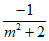 。
。
所以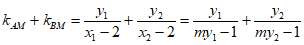
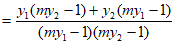 =
=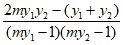 =
=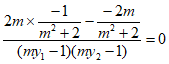 。
。
18. (1)设”一次从纸箱中摸出两个小球,恰好摸出2个红球”为事件A。
则P(A)=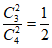 。
。
(2)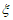 可能取0,1,2,3,4。
可能取0,1,2,3,4。
P(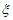 =0)=C
=0)=C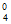 (
(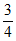 )0(1-
)0(1-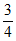 )4=
)4=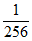 ,P(
,P(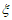 =1)=C
=1)=C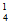 (
(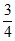 )1(1-
)1(1-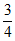 )3=
)3=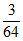 ,
,
P(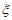 =2)=C
=2)=C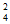 (
(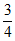 )2(1-
)2(1-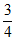 )2=
)2=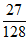 ,P(
,P(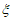 =3)=C
=3)=C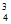 (
(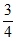 )3(1-
)3(1-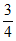 )1=
)1=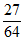 ,
,
P(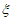 =4)=C
=4)=C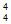 (
(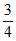 )4(1-
)4(1-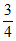 )0=
)0=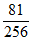 。
。
所以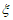 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
(3)15。
19. (1)由题意知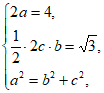 解得
解得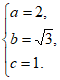
所以椭圆C的方程是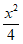 +
+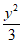 =1。
=1。
(2)由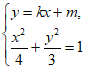 得
得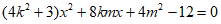 。
。
因为动直线l与椭圆C有且只有一个公共点M(x0,y0),
所以m≠0,且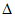 =0,
=0,
即64k2m2-4(4k2+3)(4m2-12)=0,化简得4k2-m2+3=0。(*)
此时x0=-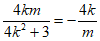 ,y0=kx0+m=
,y0=kx0+m=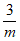 ,所以M(–
,所以M(–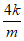 ,
,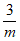 )。
)。
由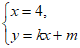
得N(4,4k+m)。
假设平面内存在定点P满足条件,由图形对称性可知,点P必在x轴上。
设P(x1,0),则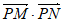 =0对满足(*)式的m,k恒成立。
=0对满足(*)式的m,k恒成立。
因为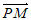 =(–
=(–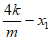 ,
,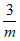 ),
),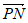 =(4-x1,4k+m),
=(4-x1,4k+m),
由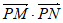 =0,得–
=0,得–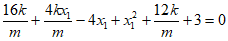 ,
,
整理,得(4x1-4)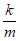 +
+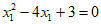 。(**)
。(**)
由于(**)式对满足(*)式的m,k恒成立,
所以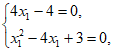 解得x1=1。
解得x1=1。
所以存在定点P(1,0),使得以MN为直径的圆恒过点M。
20. (1)-64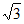 ;(2)
;(2)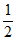 。
。