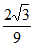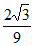本试卷共150分。考试时长120分钟。
第一部分
(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合A={x|-1<x<3},B={x|0<x≤4},则A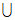 B=
B=
A. (0,3) B. (-1,4) C. (0,4] D. (-1,4]
2. 在复平面内,复数z所对应的点的坐标为(1,-1),则z·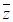 =
=
A. 2 B. -2i C. 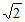 D. 2i
D. 2i
3. 已知f(x)为奇函数,其局部图象如图所示,那么
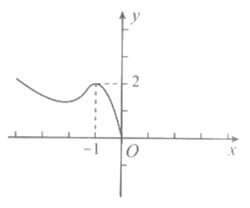
A. f(2)=2 B. f(2)=-2
C. f(2)>-2 D. f(2)<-2
4. 已知A(4,8),B(2,4),C(3,y)三点共线,则y的值为
A. 4 B. 5 C. 6 D. 7
5. 已知双曲线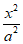 –
–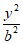 =1的焦距等于实轴长的2倍,则其渐近线的方程为
=1的焦距等于实轴长的2倍,则其渐近线的方程为
A. 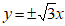 B. y=
B. y=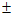 2x
2x
C. 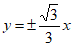 D. y=±
D. y=±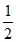 x
x
6. 已知半径为2的圆经过点(1,0),其圆心到直线3x-4y+12=0的距离的最小值为
A. 0 B. 1 C. 2 D. 3
7. 已知函数f(x)=sin2x,x∈[a,b],则“b-a≥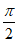 “是“f(x)的值域为[-1,1]”的
“是“f(x)的值域为[-1,1]”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 被誉为信息论之父的香农提出了一个著名的公式:C=Wlog2(1+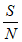 ),其中C为最大数据传输速率,单位为bit/s;W为信道带宽,单位为Hz;
),其中C为最大数据传输速率,单位为bit/s;W为信道带宽,单位为Hz;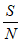 为信噪比。香农公式在5G技术中发挥着举足轻重的作用。
为信噪比。香农公式在5G技术中发挥着举足轻重的作用。
当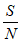 =99,W=2000Hz时,最大数据传输速率记为Cl;当
=99,W=2000Hz时,最大数据传输速率记为Cl;当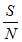 =9999,W=3000Hz时,最大数据传输速率记为C2,则
=9999,W=3000Hz时,最大数据传输速率记为C2,则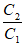 为
为
A. 1 B. 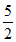 C.
C. 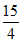 D. 3
D. 3
9. 设函数f(x)和g(x)的定义域为D,若存在非零实数c∈D,使得f(c)+g(c)=0,则称函数f(x)和g(x)在D上具有性质P。
现有三组函数:
①f(x)=x,g(x)=x2
②f(x)=2-x,g(x)=-ex
③f(x)=-x2,g(x)=2x
其中具有性质P的是
A. ①② B. ①③ C. ②③ D. ①②③
10. 在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为BD1,B1C1的中点,点P在正方体的表面上运动,且满足MP⊥CN,则下列说法正确的是
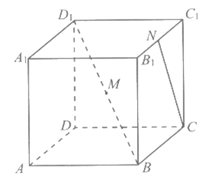
A. 点P可以是棱BB1的中点
B. 线段MP的最大值为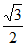
C. 点P的轨迹是正方形
D. 点P轨迹的长度为2+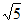
第二部分
(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
11. (x-2)5的展开式中x的系数是________。
12. 数列{an}是公差为-2的等差数列,记{an}的前n项和为Sn,且a1,a3,a4成等比数列,则a1=________;Sn=________。
13. 一个三棱锥的三视图如图所示,该三棱锥中最长棱的长度为________。
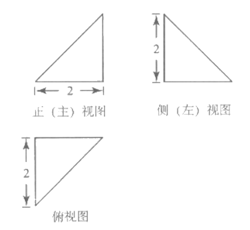
14. 已知抛物线C:y2=2px(p>0)的焦点为F,过点M(-l,4)作y轴的垂线交抛物线C于点A,且满足|AF|=|AM|,则抛物线C的方程为________;设直线AF交抛物线C于另一点B,则点B的纵坐标为________。
15. 炎炎夏日,冰激凌成为非常受欢迎的舌尖上的味道。某商店统计了一款冰激凌6月份前6天每天的供应量和销售量,结果如下表:
6月1日 | 6月2日 | 6月3日 | 6月4日 | 6月5日 | 6月6日 | |
供应量 | 90 | 100 | 90 | 100 | 90 | 100 |
销售量 | 80 | 90 | 85 | 80 | 90 | 85 |
记V(t)为6月t日冰激凌的供应量,W(t)为6月t日冰激凌的销售量,其中t=l,2,…,30。
用销售指数P(t,n)=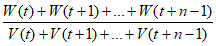 ×100%,(n≥1,n∈N)来评价从6月t日开始连续n天的冰激凌的销售情况。当n=1时,P(t,1)表示6月t日的日销售指数。
×100%,(n≥1,n∈N)来评价从6月t日开始连续n天的冰激凌的销售情况。当n=1时,P(t,1)表示6月t日的日销售指数。
给出下列四个结论:
①在6月1日至6日这6天中,P(4,1)最小,P(5,1)最大;
②在6月1日至6日这6天中,日销售指数越大,说明该天冰激凌的销售量越大;
③P(1,3)=P(4,3);
④如果6月7日至12日冰激凌每天的供应量和销售量与6月1日至6日每天的供应量和销售量对应相等,则对任意t∈{l,2,3,4,5,6,7},都有P(t,6)=P(1,12)。
其中所有正确结论的序号是_______。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
如图,在直三棱柱ABC-A1B1C1中,AB=AC=2,AA1=4,AB⊥AC,BE⊥AB1交AA1于点E,D为CC1的中点。
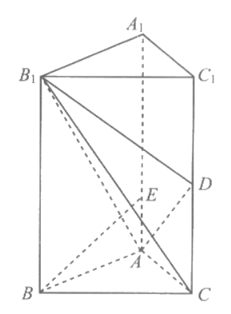
(I)求证:BE⊥平面AB1C;
(II)求二面角C-AB1-D的余弦值。
17. (本小题13分)
已知△ABC的面积为4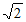 ,再从条件①、条件②这两个条件中选择一个作为已知,求:
,再从条件①、条件②这两个条件中选择一个作为已知,求:
(I)b和c的值;
(II)sin(A-B)的值。
条件①:a=6,cosC=-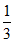 ;条件②:A=C,cosB=-
;条件②:A=C,cosB=-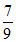 。
。
注:如果选择条件①和条件②分别解答,按第一个解答计分。
18. (本小题14分)
防洪工程对防洪减灾起着重要作用,水库是我国广泛采用的防洪工程之一,既有滞洪作用又有蓄洪作用。北京地区2010年至2019年每年汛末(10月1日)水库的蓄水量数据如下:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
蓄水量(亿立方米) | 11.25 | 13.25 | 13.58 | 17.4 | 12.4 | 12.1 | 18.3 | 26.5 | 34.3 | 34.1 |
(I)从2010年至2019年的样本数据中随机选取连续两年的数据,求这两年蓄水量数据之差的绝对值小于1亿立方米的概率;
(II)从2014年至2019年的样本数据中随机选取两年的数据,设X为蓄水量超过33亿立方米的年份个数,求随机变量X的分布列和数学期望;
(III)由表中数据判断从哪年开始连续三年的水库蓄水量方差最大?(结论不要求证明)
19. (本小题15分)
已知函数f(x)=x3-x。
(I)求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)求函数f(x)的单调区间和极值;
(III)设函数t(x)=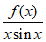 -2,x∈(0,
-2,x∈(0,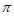 ),试判断t(x)的零点个数,并证明你的结论。
),试判断t(x)的零点个数,并证明你的结论。
20. (本小题15分)
已知椭圆C=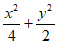 =1。
=1。
(I)求椭圆C的离心率和长轴长;
(II)已知直线y=kx+2与椭圆C有两个不同的交点A,B,P为x轴上一点。是否存在实数k,使得△PAB是以点P为直角顶点的等腰直角三角形?若存在,求出k的值及点P的坐标;若不存在,说明理由。
21. (本小题15分)
对于数列{an},定义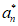 =
=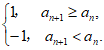 设{
设{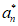 }的前n项和为
}的前n项和为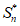 。
。
(I)设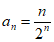 ,写出
,写出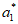 ,
,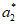 ,
,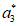 ,
,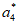 ;
;
(II)证明:“对任意n∈N*,有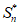 =an+1-a1“的充要条件是“对任意n∈N*,有|an+1-an|=1″;
=an+1-a1“的充要条件是“对任意n∈N*,有|an+1-an|=1″;
(III)已知首项为0,项数为m+1(m≥2)的数列{an}满足:
①对任意1≤n≤m且n∈N*,有an+l-an∈{-1,0,1};②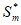 =am。
=am。
求所有满足条件的数列{an}的个数。
参考答案
一、选择题(共10小题,每小题4分,共40分)
1. D 2. A 3. C 4. C
5. A 6. B 7. B 8. D
9. B 10. D
二、填空题(共5小题,每小题5分,共25分)
11. 80 12. 8,-n2+9n
13. 2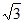 14. y2=4x,-1
14. y2=4x,-1
15. ①④
注:第(12)和(14)题第一空3分,第二空2分。第(15)题全部选对得5分,不选或有错选得0分,其他得3分。
三、解答题(共6小题,共85分)
16. (共13分)
解:(I)因为三棱柱ABC-A1B1C1为直三棱柱,所以AA1⊥平面ABC,
所以AA1⊥AC。 ……………1分
因为AC⊥AB,AB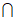 AA1=A,所以AC⊥平面AA1B1B。……………3分
AA1=A,所以AC⊥平面AA1B1B。……………3分
因为BE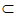 平面AA1B1B,所以AC⊥BE。……………4分
平面AA1B1B,所以AC⊥BE。……………4分
因为BE⊥AB1,AC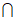 AB1=A,
AB1=A,
所以BE⊥平面AB1C。 ……………5分
(II)由(I)知AB,AC,AA1两两垂直,
如图建立空间直角坐标系A-xyz。
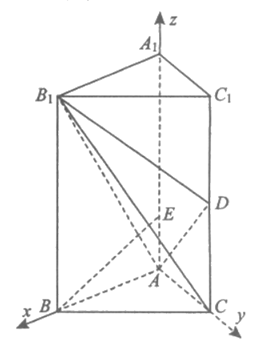
则A(0,0,0),B1(2,0,4),D(0,2,2),B(2,0,0)。
……………7分
设E(0,0,a),所以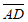 =(0,2,2),
=(0,2,2),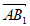 =(2,0,4),
=(2,0,4),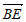 =(-2,0,a),
=(-2,0,a),
因为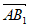 ⊥
⊥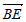 ,所以4a-4=0,即a=1。 ……………8分
,所以4a-4=0,即a=1。 ……………8分
所以平面AB1C的一个法向量为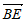 =(-2,0,1)。 ……………9分
=(-2,0,1)。 ……………9分
设平面AB1D的法向量为n=(x,y,z),
所以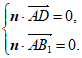 所以
所以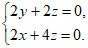 即
即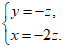 ………10分
………10分
令z=-1,则x=2,y=1,
所以平面AB1D的一个法向量为n=(2,1,-1)。 ……………11分
所以cos<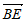 ,n>=
,n>=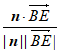 =
=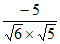 =-
=-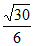 。 ………12分
。 ………12分
由已知,二面角C-AB1-D为锐角,
所以二面角C-AB1-D的余弦值为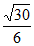 。 ……………13分
。 ……………13分
17. (共13分)
若选择条件①:
解:(I)在△ABC中,因为cosC=-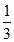 ,
,
所以C∈(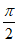 ,
,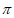 ),sinC=
),sinC=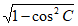 =
=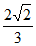 。………2分
。………2分
因为S=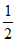 absinC=4
absinC=4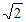 ,a=6,所以b=2。 ……………4分
,a=6,所以b=2。 ……………4分
由余弦定理,c2=a2+b2-2abcosC=48, ……………5分
所以c=4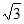 。 ……………6分
。 ……………6分
(II)由正弦定理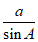 =
=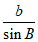 =
=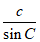 ,可得
,可得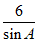 =
=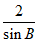 =
=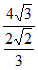 。……7分
。……7分
所以sinA=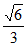 ,sinB=
,sinB=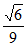 。 ………9分
。 ………9分
因为A,B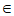 (0,
(0,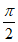 ),所以cosA=
),所以cosA=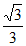 ,cosB=
,cosB=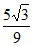 。 ………11分
。 ………11分
所以sin(A-B)=sinAcosB-cosAsinB
=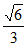 ×
×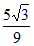 –
–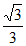 ×
×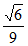 =
=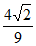 。 …………13分
。 …………13分
若选择条件②:
解:(I)在△ABC中,因为A=C,所以a=c。
因为cosB=-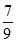 ,所以B∈(
,所以B∈(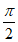 ,
, ),sinB=
),sinB=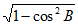 =
=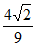 。………2分
。………2分
因为S=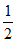 acsinB=
acsinB=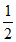 c2×
c2×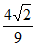 =4
=4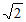 ,
,
所以a=c=3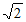 。 ……………4分
。 ……………4分
由余弦定理,b2=a2+c2-2accosB=64,所以b=8。 ……………6分
(II)由正弦定理得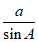 =
=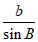 ,
,
所以sinA=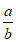 sinB=
sinB=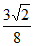 ×
×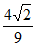 =
=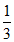 . ………8分
. ………8分
因为A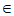 (0,
(0,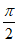 ),所以cosA=
),所以cosA=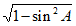 =
=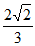 。 ………10分
。 ………10分
所以sin(A-B)=sinAcosB-cosAsinB
=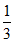 ×(-
×(-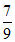 )-
)-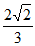 ×
×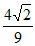 =-
=-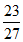 。 ………13分
。 ………13分
18. (共14分)
解:(I)设事件A为“连续两年的蓄水量数据之差的绝对值小于1亿立方米“,
从2010年到2019年的样本数据中随机选取连续两年共有9种可能,…2分
由图表可知,事件A包含“2011年和2012年“,“2014年和2015年“,“2018年和2019年“。 ……………3分
所以P(A)=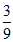 =
=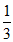 。 ……………4分
。 ……………4分
(II)由表可知,2014到2019年的样本数据中,蓄水量超过33亿立方米有2年,
蓄水量不超过33亿立方米有4年。
随机变量X的所有可能取值为0,1,2。 ……………5分
P(X=0)=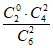 =
=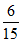 =
=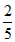 ,P(X=1)=
,P(X=1)=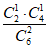 =
=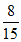 ,
,
P(X=2)=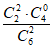 =
=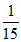 ………8分
………8分
所以随机变量X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
……………9分
所以E(X)=0×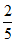 +1×
+1×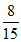 +2×
+2×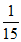 =
=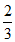 。 ……………11分
。 ……………11分
(III)从2016年开始连续三年的水库蓄水量方差最大。 ……………14分
19. (共15分)
解:(I)由f(x)=x3-x,得f ‘(x)=3x2-1。 ……………1分
因为f(1)=0,f ‘(1)=2, ……………3分
所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-2。 …………4分
(II)令f ‘(x)=0,得3x2-1=0,解得x=-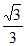 或x=
或x=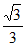 。
。
当x变化时,f(x)和f ‘(x)变化情况如下表:
x | (– | – | (– |
| ( |
f ‘(x) | + | 0 | – | 0 | + |
f(x) | ↗ |
| ↘ | – | ↗ |
……7分
所以,f(x)的单调递减区间是(–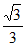 ,
,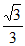 ),单调递增区间是(-∞,–
),单调递增区间是(-∞,–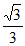 ),(
),(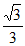 ,+∞);
,+∞);
f(x)在x=-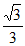 处取得极大值
处取得极大值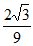 ,在x=
,在x=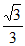 处取得极小值–
处取得极小值–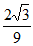 。
。
(III)x∈(0,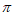 ),t(x)=0,即
),t(x)=0,即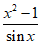 -2=0,
-2=0,
等价于x2-1-2sinx=0。 ……………10分
设g(x)=x2-1-2sinx,x∈(0,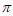 ),则g’(x)=2x-2cosx。
),则g’(x)=2x-2cosx。
①当x∈[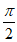 ,
,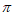 )时,g’(x)>0,g(x)在区间[
)时,g’(x)>0,g(x)在区间[ ,
,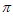 )上单调递增。
)上单调递增。
又g(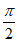 )=
)=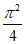 -3<0,g(
-3<0,g(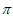 )=
)=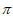 2-l>0,
2-l>0,
所以g(x)在区间[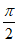 ,
,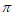 )上有一个零点。 ……………11分
)上有一个零点。 ……………11分
②当x∈(0,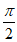 )时,设h(x)=g’(x)=2x-2cosx。
)时,设h(x)=g’(x)=2x-2cosx。
h’(x)=2+2sinx>0,所以g’(x)在区间(0,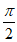 )上单调递增。………12分
)上单调递增。………12分
又g’(0)=-2<0,g’(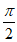 )=
)=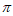 >0,
>0,
所以存在x0∈(0,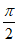 ),使得g’(x0)=0。
),使得g’(x0)=0。
所以,当x∈(0,x0)时,g’ (x)<0,g(x)单调递减;
当x∈(x0,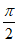 )时,g’(x)>0,g(x)单调递增。· ……………13分
)时,g’(x)>0,g(x)单调递增。· ……………13分
又g(0)=-1<0,g(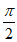 )=
)=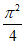 -3<0,
-3<0,
所以g(x)在区间(0,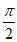 )上无零点。 ……………14分
)上无零点。 ……………14分
综上所述,函数t(x)在定义域内只有一个零点。 ……………15分
20. (共15分)
解:(I)由题意:a2=4,b2=2,所以a=2。 ……………1分
因为a2=b2+c2,所以c2=2,c=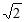 。 ……………2分
。 ……………2分
所以e=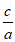 =
=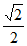 。 ……………3分
。 ……………3分
所以椭圆C离心率为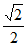 ,长轴长为4。 ……………4分
,长轴长为4。 ……………4分
(II)联立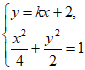 消y整理得:(2k2+1)x2+8kx+4=0。 ……………5分
消y整理得:(2k2+1)x2+8kx+4=0。 ……………5分
因为直线与椭圆交于A,B两点,故△>0,解得k2>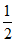 。 ……………6分
。 ……………6分
设A(xl,yl),B(x2,y2),则x1+x2=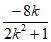 ,x1x2=
,x1x2=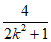 。………8分
。………8分
设AB中点G(x0,y0),
则x0=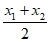 =
=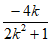 ,y0=kx0+2=
,y0=kx0+2=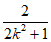 ,
,
故G(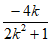 ,
,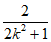 )。 ………9分
)。 ………9分
假设存在k和点P(m,0),使得△PAB是以P为直角顶点的等腰直角三角形,
则PG⊥AB,故kPG·kAB=-1,
所以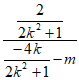 ×k=-l,解得m=
×k=-l,解得m=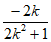 ,故P(
,故P(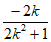 ,0)。……10分
,0)。……10分
又因为∠APB=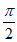 ,所以
,所以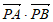 =0。
=0。
所以(x1-m,y1)·(x2-m,y2)=0,即(x1-m)(x1-m)+y1y2=0。
整理得(k2+1)x1x2+(2k-m)(x1+x2)+m2+4=0。
所以(k2+1)·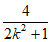 -(2k-m)·
-(2k-m)·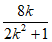 +m2+4=0, ………12分
+m2+4=0, ………12分
代入m=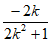 ,整理得k4=1,即k2=1。 ……………14分
,整理得k4=1,即k2=1。 ……………14分
当k=-1时,P点坐标为(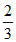 ,0);当k=1时,P点坐标为(–
,0);当k=1时,P点坐标为(–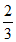 ,0)。
,0)。
此时,△PAB是以P为直角顶点的等腰直角三角形。 ……………15分
21. (共15分)
解:(I)因为a1=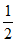 ,a2=
,a2=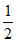 ,a3=
,a3=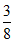 ,a4=
,a4=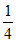 ,a5=
,a5=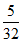 ,
,
根据题意可得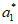 =1,
=1,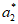 =-1,
=-1,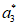 =-1,
=-1,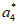 =-1。 ……………4分
=-1。 ……………4分
(II)必要性:对n=1,有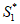 =a2-a1,因此|a2-a1|=|
=a2-a1,因此|a2-a1|=|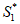 |=|
|=|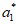 |=1。 ……5分
|=1。 ……5分
对任意n∈N*且n≥2,有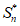 =an+1-a1,
=an+1-a1,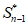 =an-a1,
=an-a1,
两式作差,得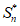 –
–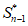 = an+1-an,即
= an+1-an,即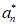 = an+1-an,
= an+1-an,
因此|an+1-an|=|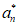 |=1。 ……………7分
|=1。 ……………7分
综上,对任意n∈N*,有|an+1-an|=1。
充分性:若对任意n∈N*,有|an+1-an|=1,则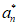 = an+1-an,
= an+1-an,
所以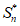 =
=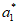 +
+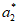 +…+
+…+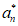 =(a2-a1)+(a3– a2)+…+( an+1-an)=an+l-a1。
=(a2-a1)+(a3– a2)+…+( an+1-an)=an+l-a1。
综上,“对任意n∈N*,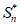 =an+1-a1,“的充要条件是“对任意n∈N*,
=an+1-a1,“的充要条件是“对任意n∈N*,
|an+1-an|=1″ …………10分
(III)构造数列{bn}:b1=0,bn+1-bn=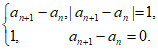
则对任意1≤n≤m且n∈N*,有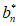 =
=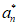 ,|bn+1-bn|=1。
,|bn+1-bn|=1。
结合(II)可知,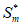 =
=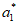 +
+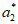 +…+
+…+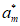 =
=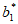 +
+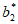 +…+
+…+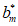 =bm+1–b1=bm+l。
=bm+1–b1=bm+l。
又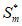 =am,因此bm+l =am。
=am,因此bm+l =am。
设a2-a1,a3-a2,…,am+1-am中有k项为0,
则am+l=a1+( a2– a1)+( a3– a2)+…+( am+1-am)
=b1+(b2-b1)+(b3-b2)+…+(bm+1-bm)-k
=bm+1-k
=am-k。
即am+l-am=-k。
因为am+1-am∈{-1,0,1},所以k=0或1。 ……………13分
若k=0,则am+l-am=0,
与a2-a1,a3-a2,…,am+1-am中有0项为0,即k=0矛盾,不符题意。
若k=1,则am+1-am=-1。
所以,当am+1-am=-1,a2– a1,a3– a2,…,am-am-1中有一项为0,其余m-2项为±l时,数列{an}满足条件。
a2– a1,a3-a2,…,am– am-1中有一项为0,共m-1种取法;其余m-2项每项有1或-1两种取法,
所以,满足条件的数列{an}的个数为(m-1)·2m-2。 ……………15分

 ,-
,-
 ,
,