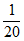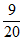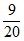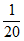本试卷满分为150分,考试时间为120分钟。
第一部分
(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合A={1,2,3},B={-l,0,2,3),则A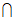 B=
B=
A. {0,l,2} B. {0,2}
C. {2,3} D. {-1,0,l,2,3}
2. 复数(1-i)2=
A. 0 B. 1 C. 2i D. -2i
3. (x+1)5的展开式中x的系数为
A. 1 B. 5 C. 10 D. 15
4. 某三棱锥的三视图如图所示,则该三棱锥的体积为
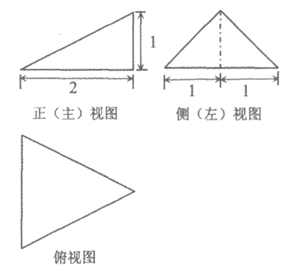
A. 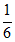 B.
B. 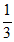 C.
C. 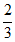 D. 2
D. 2
5. 若抛物线y2=4x上的点A到焦点的距离为10,则点A到y轴的距离是
A. 6 B. 7 C. 8 D. 9
6. “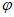 =
=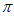 “是“函数y=sin(x+
“是“函数y=sin(x+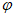 )为奇函数“的
)为奇函数“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
7. 直线l:y=kx+1与圆C:x2+(y-1)2=4的位置关系是
A. 相切 B. 相交 C. 相离 D. 不确定
8. 等差数列{an}的首项为1,公差不为0,若a1,a2,a4成等比数列,则{an}前5项的和为
A. 10 B. 15 C. 21 D. 28
9. 已知函数f(x)=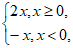 则函数y=f(x)-2|x|的零点个数是
则函数y=f(x)-2|x|的零点个数是
A. 0 B. 1 C. 2 D. 3
10. 斐波那契螺线又叫黄金螺线,广泛应用于绘画、建筑等,这种螺线可以按下列方法画出:如图,在黄金矩形ABCD(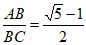 )中作正方形ABFE,以F为圆心,AB长为半径作圆弧
)中作正方形ABFE,以F为圆心,AB长为半径作圆弧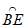 ;然后在矩形CDEF中作正方形DEHG,以H为圆心,DE长为半径作圆弧
;然后在矩形CDEF中作正方形DEHG,以H为圆心,DE长为半径作圆弧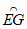 ;……;如此继续下去,这些圆弧就连成了斐波那契螺线。
;……;如此继续下去,这些圆弧就连成了斐波那契螺线。
记圆弧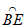 ,
,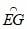 ,
,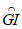 的长度分别为l,m,n,对于以下四个命题:
的长度分别为l,m,n,对于以下四个命题:
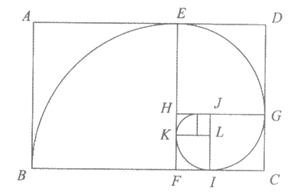
①l=m+n ②m2= l·n
③2m= l +n ④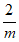 =
=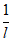 +
+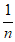
其中正确的是
A. ①② B. ①④ C. ②③ D. ③④
第二部分
(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
11. 函数f(x)=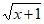 +lnx的定义域为_________。
+lnx的定义域为_________。
12. 已知平面向量a=(2,1),b=(4,y),且a∥b,则实数y=_________。
13. 已知双曲线C的两个焦点为(-3,0),(3,0),一个顶点是(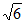 ,0),则C的标准方程为_________;C的焦点到其渐近线的距离是_________。
,0),则C的标准方程为_________;C的焦点到其渐近线的距离是_________。
14. 若函数f(x)=sin(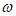 x)+cos(
x)+cos(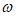 x +
x +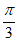 )的一个周期是
)的一个周期是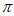 ,则常数
,则常数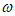 的一个取值可以为_________。
的一个取值可以为_________。
15. 从4G到5G通信,网络速度提升了40倍。其中,香农公式C=Wlog2(1+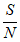 )是被广泛公认的通信理论基础和研究依据,它表示:在受噪声干扰的信道中,最大信息传递率C取决于信道带宽W、信道内信号的平均功率S、信道内部的高斯噪声功率N的大小,其中
)是被广泛公认的通信理论基础和研究依据,它表示:在受噪声干扰的信道中,最大信息传递率C取决于信道带宽W、信道内信号的平均功率S、信道内部的高斯噪声功率N的大小,其中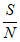 叫做信噪比。
叫做信噪比。
根据香农公式,以下说法正确的是_________。(参考数据:lg5≈0.6990)
①若不改变信噪比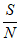 ,而将信道带宽W增加一倍,则C增加一倍;
,而将信道带宽W增加一倍,则C增加一倍;
②若不改变信道带宽W和信道内信号的平均功率S,而将高斯噪声功率N降低为原来的一半,则C增加一倍;
③若不改变带宽W,而将信噪比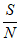 从255提升至1023,C增加了25%;
从255提升至1023,C增加了25%;
④若不改变带宽W,而将信噪比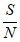 从999提升至4999,C大约增加了23.3%。
从999提升至4999,C大约增加了23.3%。
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16. (本小题13分)
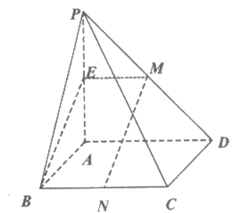
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,M,N分别为棱PD,BC的中点,PA=AB=2。
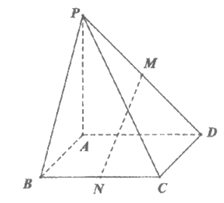
(I)求证:MN∥平面PAB;
(II)求直线MN与平面PCD所成角的正弦值。
17. (本小题13分)
在△ABC中,c=2,C=30°。再从条件①、条件②、条件③这三个条件中选择一个作为已知,使其能够确定唯一的三角形,求:
(I)a的值;
(IT)△ABC的面积。
条件①:2b=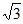 a;
a;
条件②:A=45°;
条件③:b=2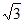 。
。
注:如果选择多个条件分别解答,按第一个解答计分。
18. (本小题14分)
在学期末,为了解学生对食堂用餐满意度情况,某兴趣小组按性别采用分层抽样的方法,从全校学生中抽取容量为200的样本进行调查。被抽中的同学分别对食堂进行评分,满分为100分。调查结果显示:最低分为51分,最高分为100分。随后,兴趣小组将男、女生的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
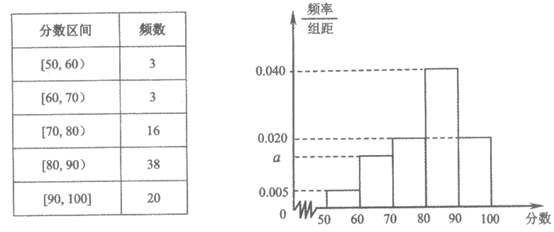
男生评分结果的频数分布表
女生评分结果的频率分布直方图
为了便于研究,兴趣小组将学生对食堂的评分转换成了“满意度情况“,二者的对应关系如下:
分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
满意度情况 | 不满意 | 一般 | 比较满意 | 满意 | 非常满意 |
(I)求a的值;
(Ⅱ)为进一步改善食堂状况,从评分在[50,70)的男生中随机抽取3人进行座谈,记这3人中对食堂“不满意“的人数为X,求X的分布列;
(III)以调查结果的频率估计概率,从该校所有学生中随机抽取一名学生,求其对食堂“比较满意“的概率。
19. (本小题15分)
已知椭圆C: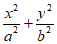 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=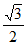 ,且经过点D(0,1)。
,且经过点D(0,1)。
(I)求椭圆C的方程。
(II)已知点O(0,0)和点A(-1,0),过点B(-4,0)的动直线l交椭圆C于M,N两点(M在N左侧),试讨论∠BAM与∠OAN的大小关系,并说明理由。
20. (本小题15分)
设函数f(x)=alnx+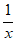 ,a∈R。
,a∈R。
(I)设l是y=f(x)图象的一条切线,求证:当a=0时,l与坐标轴围成的三角形的面积与切点无关;
(II)若函数g(x)=f(x)-x在定义域上单调递减,求a的取值范围。
21. (本小题15分)
对于数列{an},若从第二项起的每一项均大于该项之前的所有项的和,则称{an}为P数列。
(I)数列{an}为-1,1,3,5,7,数列{bn}为-l,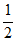 ,–
,–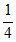 ,
,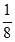 。判断数列{an},{bn}是否为P数列,并说明理由;
。判断数列{an},{bn}是否为P数列,并说明理由;
(II)设数列{an}是首项为2的P数列,其前n项和为Sn(n∈N*)。
求证:当n≥2时,Sn>2n;
(III)设无穷数列{an}是首项为a(a>0),公比为q的等比数列,有穷数列{bn},{cn}是从{an}中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为T1,T2。
若T1=T2。判断{an}是否为P数列,并说明理由。
参考答案
一、选择题:本大题共10个小题,每小题4分,共40分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | D | B | C | D | A | B | B | C | A |
二、填空题:本大题共5个小题,每小题5分,共25分。
11. (0,+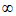 ); 12. 2; 13.
); 12. 2; 13. 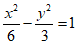 ,
,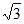 ;
;
14. 2;(答案不唯一) 15. ①③④。
三、解答题:本大题共6个小题,共85分。解答题应写出文字说明,证明过程或演算步骤。
16. (本小题13分)
解:(I)在四棱锥P-ABCD中,
取PA的中点E,连接EB、EM,
因为M是PD的中点,
所以EM∥AD,且EM=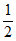 AD。
AD。
…………2分
又因为底面ABCD是正方形,N是BC的中点,
所以BN∥AD,且BN=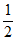 AD。
AD。
所以EM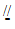 BN。
BN。
所以四边形MNBE是平行四边形。 …………4分
所以MN∥EB。
由于EB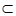 平面PAB,
平面PAB,
MN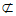 平面PAB,
平面PAB,
所以MN∥平面PAB。 …………6分
(II)因为底面ABCD是正方形,所以AB⊥AD。
又因为PA⊥平面ABCD。
所以以点A为坐标原点,AB、AD、AP分别为x、y、z轴,
如图建立空间直角坐标系。 …………8分
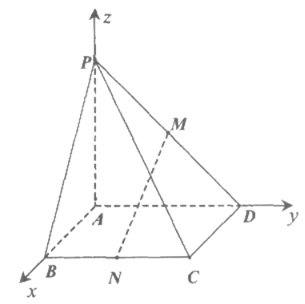
A(0,0,0),C(2,2,0),D(0,2,0),P(0,0,2),M(0,1,1),N(2,1,0)。
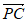 =(2,2,-2),
=(2,2,-2),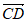 =(-2,0,0),
=(-2,0,0),
设平面PCD的法向量为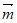 =(x,y,z)。
=(x,y,z)。
有: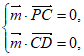 即
即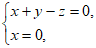 令y=1,则z=1,所以
令y=1,则z=1,所以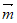 =(0,1,1)。
=(0,1,1)。
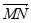 =(2,0,-1)。
=(2,0,-1)。
设直线MN与平面PCD所成角为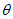 。
。
有: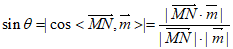
=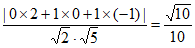 。
。
所以直线MN与平面PCD所成角的正弦值为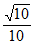 。…………13分
。…………13分
17. (本小题13分)
选择条件①:2b=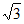 a
a
解:(I)在△ABC中,
因为2b=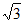 a,
a,
所以b=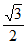 a。
a。
因为c=2,C=30°。
根据余弦定理:cosC=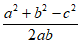 ,得cos30°=
,得cos30°=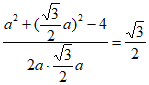 ,
,
整理,得a2=16,
由于a>0,
所以a=4。……… 7分
(II)由(I)可知,b=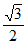 a=2
a=2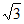 。
。
因为a=4,c=2,
所以a2=b2+c2。
所以A=90°。
因此,△ABC是直角三角形。
所以S=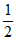 bc=
bc=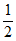 ×2
×2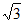 ×2=2
×2=2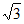 。 ……13分
。 ……13分
选择条件②:A=45°。
解:(I)在△ABC中,
因为A=45°,C=30°,c=2。
根据正弦定理: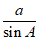 =
=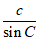 ,
,
所以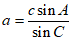 =
=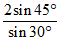 =
=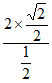 =2
=2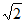 。 ……7分
。 ……7分
(II)在△ABC中,
因为sinB=sin(A+C)。
所以sinB=sin(30°+45°)=sin30°cos45°+cos30°sin45°=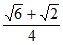 。
。
所以S=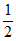 acsinB=
acsinB=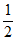 ×2
×2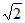 ×2×
×2×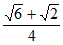 =
=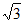 +1。 ……13分
+1。 ……13分
选择条件③:不给分
18. (本小题14分)
解:(I)因为(0.005+a+0.020+0.040+0.020)×10=1,
所以a=0.015。 …………3分
(II)依题意,随机变量X的所有可能取值为0,1,2,3。 …………4分
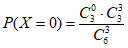 =
=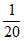 ;
;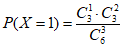 =
=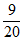 ;
;
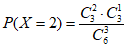 =
=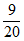 ;
;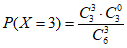 =
=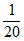 。
。
所以随机变量X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
…………9分
(III)设事件A=”随机抽取一名学生,对食堂‘比较满意“‘。 …………10分
因为样本人数200人,其中男生共有80人,
所以样本中女生共有120人。
由频率分布直方图可知,
女生对食堂“比较满意“的人数共有:120×0.020×10=24人。…………12分
由频数分布表,可知男生对食堂“比较满意“的共有16人,
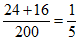 。
。
所以随机抽取一名学生,对食堂“比较满意“的概率为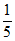 。…………14分
。…………14分
19. (本小题15分)
解:(I)由已知b=1,e=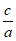 =
=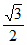 , …………2分
, …………2分
又a2=b2+c2,解得a=2,b=1。 …………5分
所以椭圆C的方程为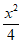 +y2=1。 …………6分
+y2=1。 …………6分
(II)依题意设直线l的方程为y=k(x+4),设M(x1,y1),N(x2,y2)。
联立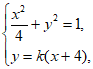 消去y,得(4k2+1)x2+32k2x+64k2-4=0,
消去y,得(4k2+1)x2+32k2x+64k2-4=0,
则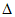 =16(1-12k2)>0,解得–
=16(1-12k2)>0,解得–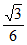 <k<
<k<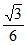 。
。
(*)
则x1+x2=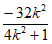 ,x1x2=
,x1x2=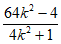 。 …………10分
。 …………10分
若x1=-1,则y1=±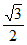 ,k=±
,k=±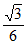 与(*)式矛盾,所以x1≠-1。
与(*)式矛盾,所以x1≠-1。
同理x2≠-1。
所以直线AM和AN的斜率存在,分别设为kAM和kAN。 …………11分
因为kAM和kAN=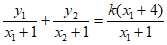 +
+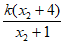 =2k+
=2k+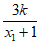 +
+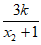
=2k+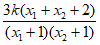 =2k+
=2k+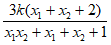
=2k+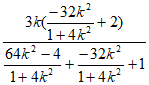 =2k+
=2k+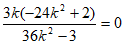
所以kAM=-kAN。
所以∠BAM=∠OAN。 …………15分
20. (本小题15分)
解:(I)当a=0时,f(x)=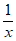 ,f ‘(x)=-
,f ‘(x)=-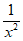 , …………2分
, …………2分
设f(x)图象上任意一点P(x0,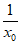 ),
),
切线l斜率为k=f ‘(x0)=-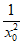 。 …………3分
。 …………3分
过点P(x0,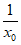 )的切线方程为y-
)的切线方程为y-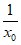 =-
=-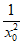 (x-x0)。
(x-x0)。
令x=0,解得y=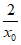 ;令y=0,解得x=2x0。 …………5分
;令y=0,解得x=2x0。 …………5分
切线与坐标轴围成的三角形面积为S=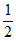 |
|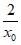 |·|2x0|=2。
|·|2x0|=2。
所以l与坐标轴围成的三角形的面积与切点无关。 …………7分
(II)由题意,函数g(x)的定义域为(0,+∞)。 …………8分
因为g(x)在(0,+∞)上单调递减, …………10分
所以g’(x)=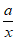 –
–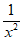 -1≤0在(0,+∞)上恒成立,
-1≤0在(0,+∞)上恒成立,
即当x∈(0,+∞),a≤x+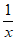 恒成立, …………12分
恒成立, …………12分
因为当x∈(0,+∞),x+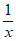 ≥2,当且仅当x=1时取等号。 …………14分
≥2,当且仅当x=1时取等号。 …………14分
所以a≤2。
所以a的取值范围为(–∞,2]。 …………15分
21. (本小题15分)
解:(I)数列{an}不是P数列,数列{bn}是P数列。 …………2分
对于数列{an},-1+l+3+5>7,所以数列{an}不是P数列;…………3分
对于数列{bn},-1<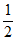 ,-1+
,-1+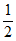 <-
<-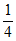 ,-1+
,-1+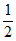 –
–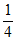 <
<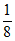 ,所以数列{bn}是P数列。
,所以数列{bn}是P数列。
…………4分
(II)由题意知,an+1>Sn,即Sn+1-Sn>Sn,即Sn+1>2Sn。
又因为S1=a1=2>0,
所以Sn>0。
所以当n≥2时,Sn=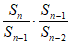 ……
……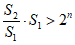
命题得证。 …………8分
(III)假设数列{an}是P数列,则a2=aq>a得q>1,
所以数列{an}是单调递增数列,且an>0,n∈N*。
(1)若数列{bn}中的元素都在数列{cn}中,则T1<T2;
(2)若数列{cn}中的元素都在数列{bn}中,则T1>T2;
(3)若数列{bn}和数列{cn}有部分公共元素,将数列{bn}和{cn}的公共元素去掉得到新的数列{bn‘}和{cn‘},
不妨设数列{bn‘}和{cn‘}中的最大元素am在数列{cn‘}中,
则数列{an}的前m-1项和Sm-1<am。
因为an>0,n∈N*,
所以数列{bn‘}中的所有项和小于等于Sm-1。
所以数列{bn‘}中的所有项和小于am。
所以T1<T2。
综上(1)(2)(3)知T1≠T2。与已知T1=T2矛盾,所以数列{an}不是P数列。
…………15分
【若有不同解法,请酌情给分】