本试卷共三道大题,25道小题,满分100分,考试时间120分钟。
一、选择题(本题共24分,每小题3分)
下面各题均有四个选项,符合题意的选项只有一个。
1. 已知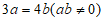 ,则下列各式正确的是
,则下列各式正确的是
A. 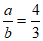 B.
B. 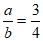 C.
C. 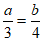 D.
D.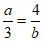
2. 在△ABC中,∠C=90°,tanA=2,则sinA的值是
A. 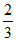 B.
B. 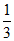 C.
C. 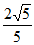 D.
D.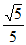
3. 如图所示,将一根长2m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是
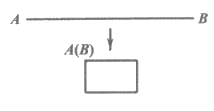
A. 正比例函数关系 B. 一次函数关系
C. 二次函数关系 D. 反比例函数关系
4. 如图,PA,PB为⊙O的两条切线,点A,B是切点,OP交⊙O于点C,交弦AB于点D,下列结论中错误的是
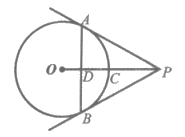
A. PA=PB B. AD=BD C. OP⊥AB D. ∠PAB=∠APB
5. 下列函数中,当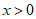 时,y随x的增大而减小的是
时,y随x的增大而减小的是
A. 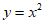 B.
B. 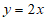 C.
C. 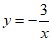 D.
D.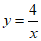
6. 不透明的袋子中有三个小球,上面分别写着数字”1“,”2“,”3“,除数字外三个小球无其他差别,从中随机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数字之和为4的概率是
A. 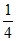 B.
B. 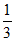 C.
C. 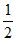 D.
D.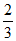
7. 大约在两千四五百年前,如图1墨子和他的学生做了世界上第一个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:”景到,在午有端,与景长,说在端”,如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是
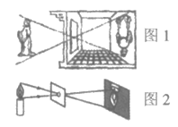
A. 3cm B. 4cm C. 6cm D.9cm
8. 已知某函数的图象过A(2,1),B(-1,-2)两点,下面有四个推断:
①若此函数的图象为直线,则此函数的图象和直线y=4x平行
②若此函数的图象为双曲线,则此函数的图象分布在第一、三象限
③若此函数的图象为抛物线,且开口向下,则此函数图象一定与y轴的负半轴相交
④若此函数的图象为抛物线,且开口向上,则此函数图象对称轴在直线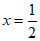 左侧
左侧
所有合理推断的序号是
A. ①③ B. ①④ C. ②③ D. ②④
二、填空题(本题共24分,每小题3分)
9. 若抛物线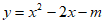 与x轴有两个交点,则m的取值范围是____________。
与x轴有两个交点,则m的取值范围是____________。
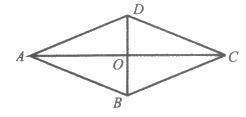
10. 如图,菱形ABCD中,AC,BD交于点O,BD=4,sin∠DAC=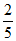 ,则菱形的边长是___________。
,则菱形的边长是___________。
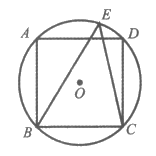
11. 如图,正方形ABCD内接于⊙O,点E在 上,则∠BEC=___________°。
上,则∠BEC=___________°。
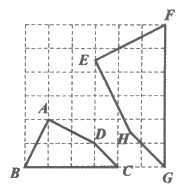
12. 如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是___________。若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是___________。
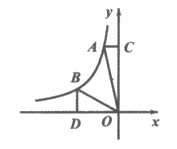
13. 如图,A,B两点在函数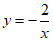 (
(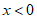 )图象上,AC垂直y轴于点C,BD垂直x轴于点D,△AOC,△BOD面积分别记为
)图象上,AC垂直y轴于点C,BD垂直x轴于点D,△AOC,△BOD面积分别记为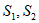 ,则
,则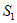 ______
______ 。(填”<”,”=”,或”>”)。
。(填”<”,”=”,或”>”)。
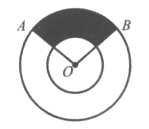
14. 如图在以点O为圆心的两个同心圆中,大圆的半径为2,小圆的半径为1,∠AOB=100°,则阴影部分的面积是______________。
15. 在平面直角坐标系xOy中,函数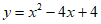 的图象G与直线
的图象G与直线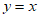 交于点A(__________),B(___________)(其中点A横坐标小于点B横坐标),记图象G在点A,B之间的部分与线段AB围成的区域(不含边界)为W,若横、纵坐标都是整数的点叫做整点,则区域W内的整点有__________个。
交于点A(__________),B(___________)(其中点A横坐标小于点B横坐标),记图象G在点A,B之间的部分与线段AB围成的区域(不含边界)为W,若横、纵坐标都是整数的点叫做整点,则区域W内的整点有__________个。
16. 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了统计表。
树苗数 | 2000 | 4000 | 6000 | 8000 | 10000 | 12000 | 14000 |
成活树苗数 | 1862 | 3487 | 5343 | 7234 | 9108 | 10931 | 12752 |
成活频率 | 0.931 | 0.8718 | 0.8905 | 0.9043 | 0.9108 | 0.9109 | 0.9109 |
根据统计表提供的信息解决下列问题:
(1)请估计树苗成活的概率是__________(精确到小数点后第3位);
(2)该地区已经移植这种树苗5万棵,估计这种树苗能成活_________万棵。
三、解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 计算:sin60°·tan30°+ 。
。
18. 已知关于x的二次函数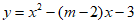 。
。
(1)该函数图象经过点(2,-3)。
①求这个二次函数的表达式及顶点坐标;
②分别求出这个二次函数图象与x轴,y轴的交点坐标;
(2)将这个二次函数的图象沿x轴平移,使其顶点恰好落在y轴上,请直接写出平移后的函数表达式。
19. 下面是小石设计的”过圆上一点作圆的切线”的尺规作图的过程。
已知:如图1,⊙O及⊙O上一点P。
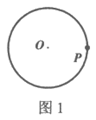
求作:直线PN,使得PN与⊙O相切。
作法:如图2。
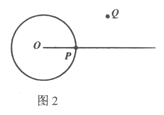
①作射线OP;
②在⊙O外取一点Q(点Q不在射线OP上),以Q为圆心,QP为半径作圆,⊙Q与射线OP交于另一点M;
③连接MQ并延长交⊙Q于点N;
④作直线PN。
所以直线PN即为所求作直线。
根据小石设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明。
证明:∵MN是⊙Q的直径,
∴∠MPN=__________°(_______________)(填推理的依据)。
∴OP⊥PN。
又∵OP是⊙O的半径,
∴PN是⊙O的切线(______________)(填推理的依据)。
20. 如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD。
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,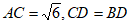 ,求AD的长。
,求AD的长。
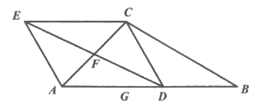
21. 在平面直角坐标系xOy中,直线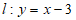 与函数
与函数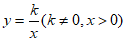 的图象交于点
的图象交于点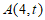 。
。
(1)求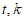 的值;
的值;
(2)点B是函数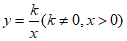 的图象上任意一点(不与点A重合),点P,Q在直线
的图象上任意一点(不与点A重合),点P,Q在直线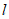 上,点P横坐标为2,若
上,点P横坐标为2,若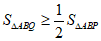 ,求点Q横坐标的取值范围。
,求点Q横坐标的取值范围。
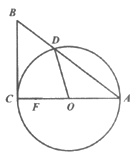
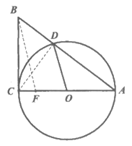
22. 如图,DO是⊙O的半径,点F是直径AC上一点,点B在AD的延长线上,连接BC,使得∠ABC=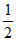 ∠AOD。
∠AOD。
(1)求证:BC是⊙O的切线;
(2)连接BF,若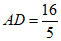 ,tan∠ABC=
,tan∠ABC=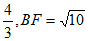 ,求CF的长。
,求CF的长。
23. 已知关于x的二次函数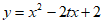 。
。
(1)求该抛物线的对称轴(用含t的式子表示);
(2)若点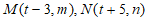 在抛物线上,则m__________n;(用”<”,”=”,或”>”填空)
在抛物线上,则m__________n;(用”<”,”=”,或”>”填空)
(3)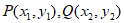 是抛物线上的任意两个点,若对于
是抛物线上的任意两个点,若对于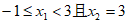 ,都有
,都有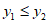 ,求t的取值范围。
,求t的取值范围。
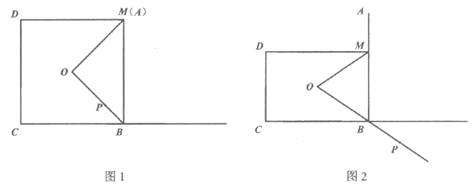
24. 已知矩形MBCD的顶点M是线段AB上一动点,AB=BC,矩形MBCD的对角线交于点O,连接MO,BO,点P为射线OB上一动点(与点B不重合),连接PM,作PN⊥PM交射线CB于点N。
(1)如图1,当点M与点A重合时,且点P在线段OB上。
①依题意补全图1;
②写出线段PM与PN的数量关系并证明。
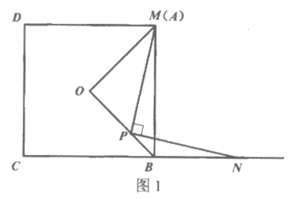
(2)如图2,若∠OMB=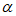 ,当点P在OB的延长线上时,请补全图形并直接写出PM与PN的数量关系。
,当点P在OB的延长线上时,请补全图形并直接写出PM与PN的数量关系。
25. 对于平面直角坐标系xOy中第一象限内的点P(x,y)和图形W,给出如下定义:
过点P作x轴和y轴的垂线,垂足分别为M,N,若图形W中的任意一点Q(a,b)满足a≤x且b≤y,则称四边形PMON是图形W的一个覆盖,点P为这个覆盖的一个特征点。例:已知A(1,2),B(3,1),则点P(5,4)为线段AB的一个覆盖的特征点。
(1)已知点C(2,3),
①在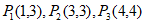 中,是△ABC的覆盖特征点的为___________;
中,是△ABC的覆盖特征点的为___________;
②若在一次函数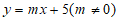 的图象上存在△ABC的覆盖的特征点,求m的取值范围。
的图象上存在△ABC的覆盖的特征点,求m的取值范围。
(2)以点D(2,4)为圆心,半径为1作圆,在抛物线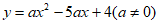 上存在⊙D的覆盖的特征点,直接写出a的取值范围________________。
上存在⊙D的覆盖的特征点,直接写出a的取值范围________________。
【试题答案】
阅卷须知:
1. 为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可。
2. 若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
3. 评分参考中所注分数,表示考生正确做到此步应得的累加分数。
一、选择题(本题共24分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | C | C | D | D | B | B | D |
二、填空题(本题共24分,每小题3分)
9. 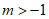 10. 5 11. 45° 12.
10. 5 11. 45° 12. 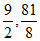 13. =
13. =
14. 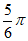 15.
15. 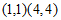 ;2 16. (1)0.911;(2)4.555
;2 16. (1)0.911;(2)4.555
三、解答题(本题共52分,第17—21题,每小题5分,第22题6分,第23—25题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 解:原式=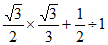 4分
4分
=1 5分
18. 解:(1)①∵该二次函数图象经过点(2,-3),
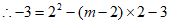 ,解得
,解得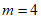 , 1分
, 1分
∴二次函数的表达式为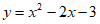 ,
,
∴二次函数顶点坐标为(1,-4)。 2分
②令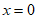 ,则
,则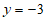 ,
,
∴该二次函数图象与x轴的交点坐标为(0,-3), 3分
令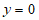 ,则
,则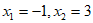 。
。
∴该二次函数图象与x轴的交点坐标为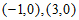 。 4分
。 4分
(2)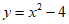 。 5分
。 5分
19. 解:(1)补全图形如下图; 2分
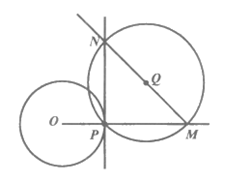
(2)90,直径所对的圆周角是直角;
经过半径的外端,并且垂直于这条半径的直线是圆的切线。 5分
20.(1)证明:∵AB∥CE,
∴∠CAD=∠ACE,∠ADE=∠CED。
∵F是AC中点,
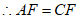 ,
,
∴△AFD≌△CFE,
∴AD=CE,
∴四边形ADCE是平行四边形。 2分
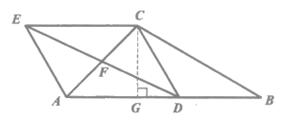
(2)解:过点C作CG⊥AB于点G,
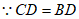 ,∠B=30°,
,∠B=30°,
∴∠DCB=∠B=30°。
∴∠CDA=60°,
在△ACG中,∠AGC=90°,AC=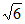 ,∠CAG=45°,
,∠CAG=45°,
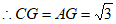 。
。
在△CGD中,∠DGC=90°,∠CDG=60°,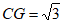 ,
,
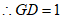 ,
,
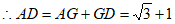 。 5分
。 5分
21. 解:(1)∵点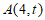 在直线
在直线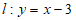 上,
上,
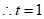 。 1分
。 1分
∵函数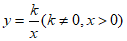 的图象经过点
的图象经过点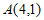
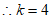 。 2分
。 2分
(2)设点B到直线AP的距离为h。
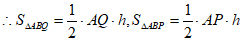
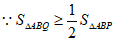 ,
,
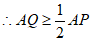 。
。
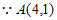 ,点P横坐标为2,
,点P横坐标为2,
如图1,当点Q在射线AP上时,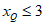 ;
;
如图2,当点Q在线段PA延长线上时,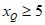 。
。
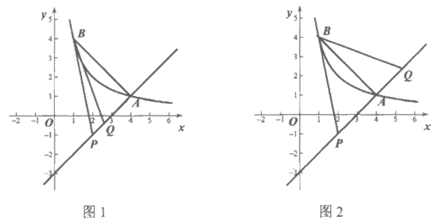
综上所述:点Q横坐标的取值范围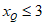 或
或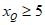 。 5分
。 5分
22. 解:(1)连接CD。
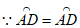 ,
,
∴∠ACD=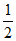 ∠AOD,
∠AOD,
∵∠ABC=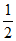 ∠AOD,
∠AOD,
∴∠ACD=∠ABC,
∵AC是⊙O直径,
∴∠ADC=90°,
∴∠ABC+∠BCD=90°,
∴∠BCA=∠BCD+∠ACD=90°,
∴BC⊥AC
∴BC是⊙O的切线。 2分
(2)在△ACD中,∠ADC=90°,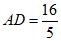 ,tan∠ACD=tan∠ABC=
,tan∠ACD=tan∠ABC=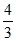 ,
,
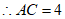 。
。
在△ABC中,∠ACB=90°,tan∠ABC=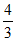 ,AC=4,
,AC=4,
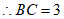 。
。
在△BCF中,∠BCF=90°,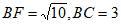 ,
,
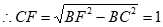 。 6分
。 6分
23. 解:(1)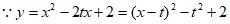 ,
,
∴抛物线的对称轴为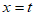 。 2分
。 2分
(2)<。 4分
(3)当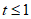 时,此时
时,此时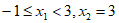 都有
都有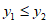 ,符合题意;
,符合题意;
当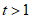 时,令
时,令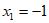 时,
时,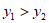 ,不符合题意。
,不符合题意。
综上所述: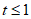 。 7分
。 7分
24. 解:(1)①补全图形如图1。 1分
②线段PM与PN的数量关系为: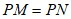 。 2分
。 2分
证明:过点P分别作PG⊥MB于G,PH⊥BC于H,
线段PN交MB于点F,如图2。
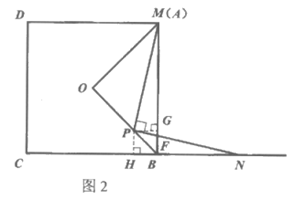
∵四边形MBCD是矩形,AB=BC,
∴四边形MBCD是正方形,
∴BO平分∠MBC,∠MBC=90°,
∵PG⊥MB,PH⊥BC,
∴PG=PH,∠PHB=∠PGM=90°,
∵PM⊥PN,∠MBC=90°,
∴∠MPN=∠GBN=90°,
∵∠MFP=∠BFN,
∴∠PMG=∠PNH,
∴△PMG≌△PNH,
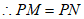 。 5分
。 5分
(2)补全图形如图3。
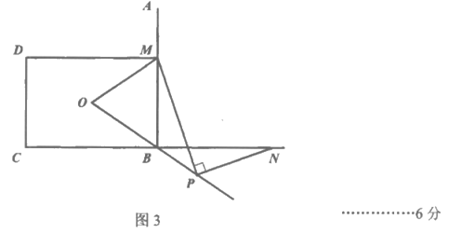
线段PM与PN的数量关系为: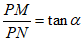 。 7分
。 7分
25. 解:(1)①P2,P3。 2分
②当m>0时,结合函数图象可知符合题意,
当m<0时,由题意得:
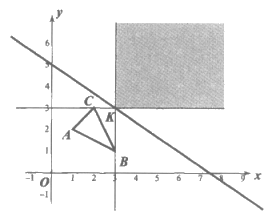
当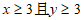 时,
时,
点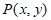 为△ABC的覆盖的特征点。
为△ABC的覆盖的特征点。
又∵点P在一次函数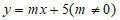 的图象上,
的图象上,
∴当直线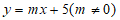 过点
过点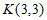 时,解得:
时,解得:
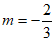 。
。
∴结合函数图象可知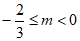 。
。
综上所述: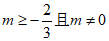 。 5分
。 5分
(2)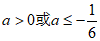 。 7分
。 7分
