本试卷共三道大题,25道小题,满分100分,考试时间120分钟。
一、选择题(本题共24分,每小题3分)
第1—8题均有四个选项,符合题意的选项只有一个。
1. 下列图形中,既是中心对称图形又是轴对称图形的是
A. 直角三角形 B. 圆 C. 等边三角形 D. 四边形
2. 在平面直角坐标系xOy中,下列函数的图象上存在点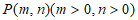 的是
的是
A. 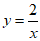 B.
B. 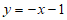 C.
C. 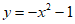 D.
D.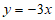
3. 若关于x的方程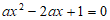 的一个根是-1,则a的值是
的一个根是-1,则a的值是
A. 1 B. -1 C. 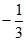 D. -3
D. -3
4. 若菱形的面积为定值,则它的一条对角线的长与另一条对角线的长满足的函数关系是
A. 正比例函数关系 B. 反比例函数关系
C. 一次函数关系 D. 二次函数关系
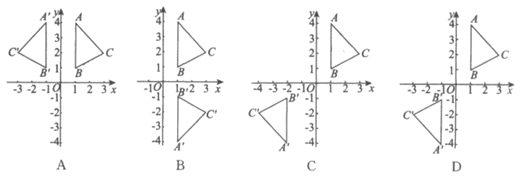
5. 在平面直角坐标系xOy中,△ABC与△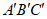 关于原点O成中心对称的是
关于原点O成中心对称的是
6. 不透明的袋子里有50张2022年北京冬奥会宣传卡片,卡片上印有会徽、吉祥物冰墩墩、吉祥物雪容融图案,每张卡片只有一种图案,除图案不同外其余均相同,其中印有冰墩墩的卡片共有n张,从中随机摸出1张卡片,若印有冰墩墩图案的概率是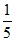 ,则n的值是
,则n的值是
A. 250 B. 10 C. 5 D. 1
7. 如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为AC,BD,设交点为P,点C,D之间有一座假山,为了测量C,D之间的距离,小明已经测量了线段AP和PD的长度,只需再测量一条线段的长度,就可以计算C,D之间的距离,小明应该测量的是
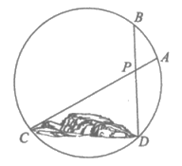
A. 线段BP B. 线段CP C. 线段AB D. 线段AD
8. 如图所示,在矩形纸片上剪下一个扇形和一个圆形,使之恰好能围成一个圆锥模型,若扇形的半径为R,圆的半径为r,则R与r满足的数量关系是
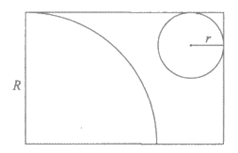
A. 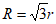 B.
B. 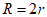 C.
C. 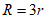 D.
D.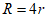
二、填空题(本题共24分,每小题3分)
9. 写出一个二次函数,使其满足:①图象开口向下;②当x>0时,y随着x的增大而减小,这个二次函数的解析式可以是______________。
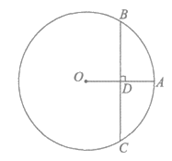
10. 如图,点A在⊙O上,弦BC垂直平分OA,垂足为D,若OA=4,则BC的长为___________。
11. A盒中有2个黄球、1个白球,B盒中有1个黄球、1个白球,这些球除颜色外无其他差别,分别从每个盒中随机取出1个球,取出的2个球都是白球的概率是____________。
12. 2017年生产1吨某种商品的成本是3 000元,由于原料价格上涨,两年后,2019年生产1吨该商品的成本是5 000元,求该种商品成本的年平均增长率,设年平均增长率为x,则所列的方程应为____________(不增加其它未知数)。
13. 在平面直角坐标系xOy中,将抛物线y=x2沿着y轴平移2个单位长度,所得抛物线的解析式为______________________。
14. 如图,△ABC是等边三角形,若将AC绕点A逆时针旋转角α后得到AC',连接BC'和CC',则∠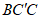 的度数为___________。
的度数为___________。
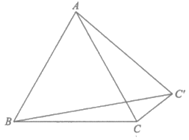
15. 已知抛物线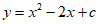 与直线
与直线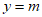 相交于A,B两点,若点A的横坐标
相交于A,B两点,若点A的横坐标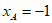 ,则点B的横坐标
,则点B的横坐标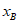 的值为__________。
的值为__________。
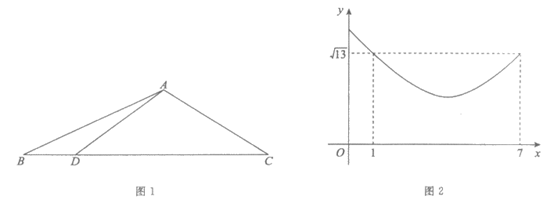
16. 如图1,在△ABC中,AB>AC,D是边BC上一动点,设B,D两点之间的距离为x,A,D两点之间的距离为y,表示y与x的函数关系的图象如图2所示,则线段AC的长为__________,线段AB的长为___________。
三、解答题(本题共52分,第17—21题,每小题5分,第22题6分,第23—25题,每小题7分)
解答应写出文字说明、演算步骤或证明过程。
17. 已知:如图,线段AB。

求作:以AB为斜边的直角△ABC,使得一个内角等于30°。
作法:①作线段AB的垂直平分线交AB于点O;
②以点O为圆心,OA长为半径画圆;
③以点B为圆心,OB长为半径画弧,与⊙O相交,记其中一个交点为C;
④分别连接AC,BC。
△ABC就是所求作的直角三角形。
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明。
证明:连接OC,
∵AB是⊙O的直径,
∴∠ACB=_________°(_____________________)(填推理的依据)。
∴△ABC是以AB为斜边的直角三角形,
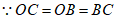 ,
,
∴△OBC是等边三角形,
∴∠COB=60°,
∴∠A=_________°。
18. 在平面直角坐标系xOy中,二次函数的图象与y轴交于点A(0,-1),且过点B(1,4),C(-2,1)。
(1)求二次函数的解析式;
(2)当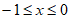 时,求y的取值范围。
时,求y的取值范围。
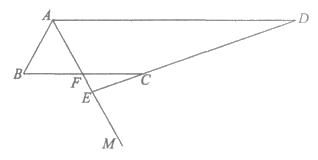
19. 如图,AM平分∠BAD,作BF∥AD交AM于点F,点C在BF的延长线上,CF=BF,DC的延长线交AM于点E。
(1)求证:AB=BF;
(2)若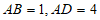 ,求
,求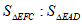 的值。
的值。
20. 关于x的一元二次方程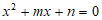 。
。
(1)若方程有两个相等的实数根,用含m的代数式表示n;
(2)若方程有两个不相等的实数根,且m=-4。
①求n的取值范围;
②写出一个满足条件的n的值,并求此时方程的根。
21. 在平面直角坐标系xOy中,已知双曲线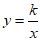 过点
过点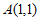 ,与直线
,与直线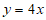 交于B,C两点(点B的横坐标小于点C的横坐标)。
交于B,C两点(点B的横坐标小于点C的横坐标)。
(1)求k的值;
(2)求点B,C的坐标;
(3)若直线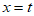 与双曲线
与双曲线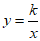 交于点
交于点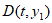 ,与直线
,与直线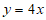 交于点
交于点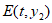 。当
。当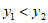 时,写出t的取值范围。
时,写出t的取值范围。
22. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,以点D为圆心,DC长为半径画⊙D。
(1)补全图形,判断直线AB与⊙D的位置关系,并证明;
(2)若BD=5,AC=2DC,求⊙D的半径。
23. 在平面直角坐标系xOy中,已知抛物线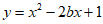 。
。
(1)若此抛物线经过点(-2,-2),求b的值;
(2)求抛物线的顶点坐标(用含b的式子表示);
(3)若抛物线上存在两点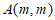 和
和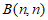 ,且
,且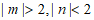 ,求b的取值范围。
,求b的取值范围。
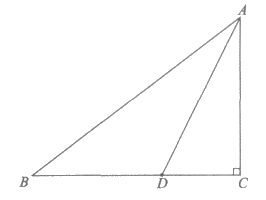
24. 在△ABC中,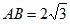 ,CD⊥AB于点D,
,CD⊥AB于点D,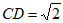 。
。
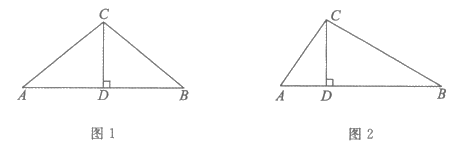
(1)如图1,当点D是线段AB的中点时,
①AC的长为______________;
②延长AC至点E,使得CE=AC,此时CE与CB的数量关系是____________,∠BCE与∠A的数量关系是_____________________;
(2)如图2,当点D不是线段AB的中点时,画∠BCE(点E与点D在直线BC的异侧),使∠BCE=2∠A,CE=CB,连接AE。
①按要求补全图形;
②求AE的长。
25. 在平面直角坐标系xOy中,⊙O的半径为1。
给出如下定义:记线段AB的中点为M,当点M不在⊙O上时,平移线段AB,使点M落在⊙O上,得到线段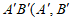 分别为点A,B的对应点)。线段
分别为点A,B的对应点)。线段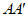 长度的最小值称为线段AB到⊙O的”平移距离”。
长度的最小值称为线段AB到⊙O的”平移距离”。
(1)已知点A的坐标为(-1,0),点B在x轴上。
①若点B与原点O重合,则线段AB到⊙O的”平移距离”为___________;
②若线段AB到⊙O的”平移距离”为2,则点B的坐标为____________;
(2)若点A,B都在直线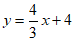 上,且
上,且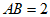 ,记线段AB到⊙O的”平移距离”为
,记线段AB到⊙O的”平移距离”为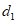 ,求
,求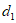 的最小值;
的最小值;
(3)若点A的坐标为(3,4),且AB=2,记线段AB到⊙O的”平移距离”为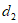 ,直接写出
,直接写出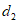 的取值范围。
的取值范围。
【试题答案】
一、选择题(本题共24分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | C | B | D | B | C | D |
二、填空题(本题共24分,每小题3分)
9. 答案不唯一,如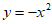 10.
10. 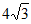 11.
11.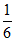
12. 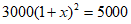 13.
13.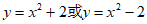
14. 30° 15. 3 16.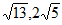
三、解答题(本题共52分,第17—21题,每小题5分,第22题6分,第23—25题,每小题7分)
17. 解:(1)补全的图形如图所示。 2分
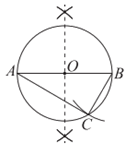
(2)90,直径所对的圆周角是直角,30。 5分
18. 解:(1)设二次函数的解析式为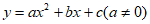 。
。
∵点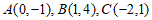 都在二次函数的图象上,
都在二次函数的图象上,
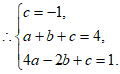
解得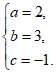
∴二次函数的解析式为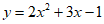 。 3分
。 3分
(2)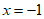 时,
时,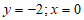 时,
时,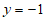 。
。
顶点坐标为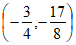 。
。
∴当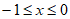 时,y的取值范围为
时,y的取值范围为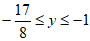 。 5分
。 5分
19.(1)证明:∵AM平分∠BAD,
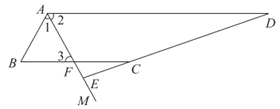
∴∠1=∠2,
∵BF∥AD,
∴∠3=∠2, 1分
∴∠1=∠3,
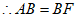 。 2分
。 2分
(2)解: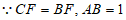 ,
,
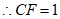 , 3分
, 3分
∵BF∥AD,
∴△EFC∽△EAD, 4分
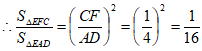 。 5分
。 5分
20. 解:(1)∵方程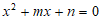 有两个相等的实数根,
有两个相等的实数根,
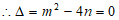 ,
,
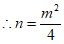 。 1分
。 1分
(2)①∵方程有两个不相等的实数根,且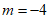 ,
,
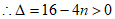 ,
,
解得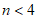 。 2分
。 2分
②答案不唯一,如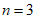 时,方程的两根为
时,方程的两根为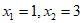 。 5分
。 5分
(参考: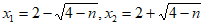 )
)
21. 解:(1)∵双曲线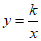 过点
过点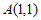 ,
,
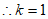 。 1分
。 1分
(2)由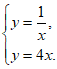
得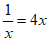 ,
,
去分母,得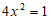 ,
,
解得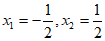 ,
,
经检验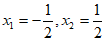 是原方程的解。
是原方程的解。
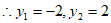 ,
,
∵点B的横坐标小于点C的横坐标,
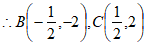 。 3分
。 3分
(3)当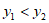 时,
时,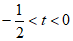 ,或
,或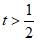 。 5分
。 5分
22. 解:(1)直线AB与⊙D相切。 1分
证明:作DE⊥AB于点E,
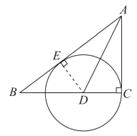
∵∠DCA=90°,AD是∠BAC的平分线,
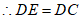 ,
,
∴直线AB与⊙D相切。 2分
(2)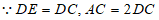 ,
,
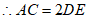 ,
,
∵∠BCA=∠BED=90°,∠B=∠B,
∴△BCA∽△BED, 3分
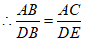 ,
,
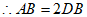 ,
,
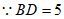 ,
,
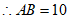 。 4分
。 4分
设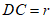 ,则
,则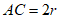 ,
,
在Rt△ABC中,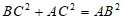 ,
,
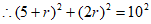 ,
,
解得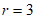 ,
,
∴⊙D的半径为3。 6分
23. 解:(1)∵抛物线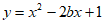 经过点
经过点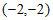 ,
,
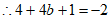 ,
,
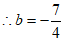 。 2分
。 2分
(2)顶点的横坐标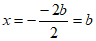 ,纵坐标
,纵坐标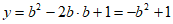 ,
,
∴顶点坐标为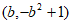 。 4分
。 4分
(3)由(1)知,当抛物线经过点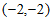 时,
时,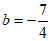 ,
,
当抛物线经过点(2,2)时,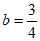 。
。
①当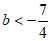 时,令
时,令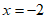 ,则
,则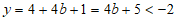 ;
;
令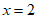 ,则
,则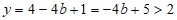 。
。
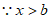 时,y随着x的增大而增大,
时,y随着x的增大而增大,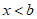 时,y随着x的增大而减小,
时,y随着x的增大而减小,
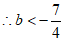 符合题意;
符合题意;
②当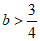 时,令
时,令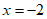 ,则
,则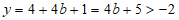 ;
;
令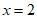 ,则
,则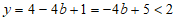 。
。
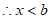 时,y随着x的增大而减小,
时,y随着x的增大而减小,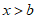 时,y随着x的增大而增大,
时,y随着x的增大而增大,
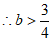 符合题意;
符合题意;
③当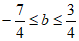 时,令
时,令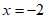 ,则
,则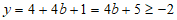 ;
;
令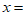 2,则
2,则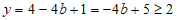 。
。
∵抛物线的开口向上,
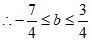 不符合题意。
不符合题意。
综上所述,b的取值范围为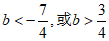 。 7分
。 7分
24. 解:(1)①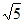 。 1分
。 1分
②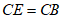 ,∠BCE=2∠A。 3分
,∠BCE=2∠A。 3分
(2)依题意补全图形,如图。 4分
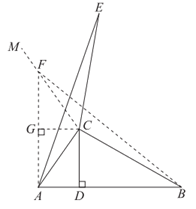
作∠ACM=∠BCE,在射线CM上截取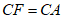 ,连接AF,FB,
,连接AF,FB,
∴∠ACM+∠FCE=∠BCE+∠FCE。
即∠ACE=∠FCB,
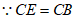 ,
,
∴△ACE≌△FCB(SAS),
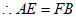 。 5分
。 5分
过点C作CG⊥AF于点G,
∴∠CGF=90°,
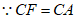 ,
,
∴∠ACF=2∠ACG,AF=2AG,
∵∠BCE=2∠BAC,
∴∠ACG=∠BAC。
∴CG∥AD,
∴∠BAF=∠CGF=90°,
∵CD⊥AB,
∴∠AGC=∠BAF=∠ADC=90°,
∴四边形ADCG是矩形,
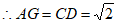 ,
,
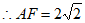 。 6分
。 6分
在Rt△BAF中,∠BAF=90°,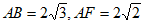 ,
,
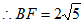 ,
,
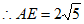 。 7分
。 7分
25. 解:(1)①线段AB到⊙O的”平移距离”为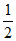 。 1分
。 1分
②点B的坐标为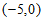 或(7,0)。 3分
或(7,0)。 3分
(2)如图,取AB的中点M,连接OM交⊙O于点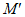 ,以
,以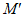 为中点作线段
为中点作线段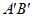 ,
,
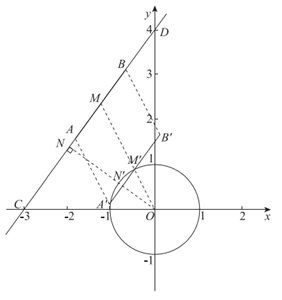
使得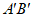 ∥AB,且
∥AB,且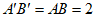 ,
,
∴四边形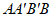 为平行四边形。 4分
为平行四边形。 4分
由题意可知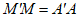 ,
,
设直线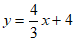 交x轴于点C,
交x轴于点C,
交y轴于点D,
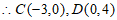 ,
,
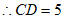 ,
,
过点O作ON⊥直线CD于点N,
交⊙O于点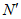 ,
,
在Rt△COD中,可得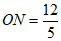 ,
,
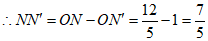 ,
,
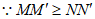 ,
,
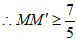 ,
,
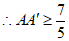 ,
,
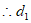 的最小值是
的最小值是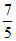 (当点M与点N重合时取得)。 5分
(当点M与点N重合时取得)。 5分
(3)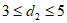 。 7分
。 7分
