(考试时间120分钟
满分100分)
一、选择题(本题共24分,每小题3分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.下列自然能源图标中,既是轴对称图形又是中心对称图形的是

2.用配方法解方程3x2-6x+2=0,将方程变为(x-m)2= 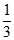 的形式,则m的值为
的形式,则m的值为
(A)9 (B) -9 (C)1 (D)-1
3.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为
(A) 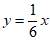 ( B) y=6x
( B) y=6x
(C)y=6x2 (D)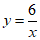
4.若⊙O的内接正n边形的边长与⊙O的半径相等,则n的值为
(A)4 (B)5 (C)6 (D)7
5.下列方程中,无实数根的方程是
( A)x2+3x=0 (B)x2+2x-1=0
(C)x2+2x+1=0 (D)x2-x+3=0
6.如图,一个可以自由转动的转盘被分为8个大小相同的扇形,颜色标注为红,黄,绿,指针的位置固定,转动转盘停止后,其中某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则下列说法正确的是
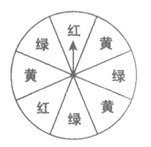
(A)指针指向黄色的概率为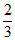
(B)指针不指向红色的概率为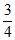
(C)指针指向红色或绿色的概率为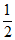
(D)指针指向绿色的概率大于指向黄色的概率
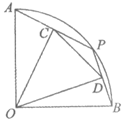
7.如图,在半径为1的扇形AOB中,∠AOB=90°,点P是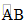 上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为
上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为
(A) 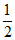 (B)
(B)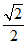
(C) 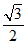 (D)1
(D)1
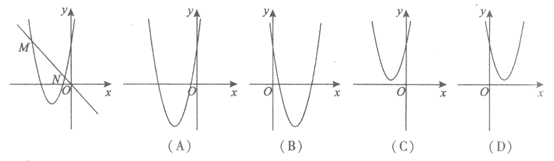
8.如图,平面直角坐标系xOy中,抛物线y=ax2+bx+c与直线y=kx交于M,N两点,则二次函数y=ax2+(b-k)x+c的图象可能是
二、填空题(本题共24分,每小题3分)
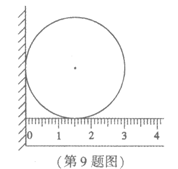
9.如图,利用垂直于地面的墙面和刻度尺,可以度量出圆的半径为________cm.
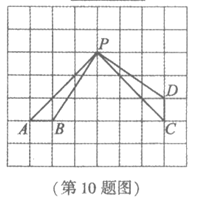
10.如图所示的正方形网格中,A,B,C,D,P是网格线交点.若∠APB=α,则∠BPC的度数为________(用含α的式子表示).
11.一元二次方程x2-3x+1=0的根为________.
12.下列事件,①通常加热到100℃,水沸腾;②人们外出旅游时,使用手机app购买景点门票:③在平面上,任意画一个三角形,其内角和小于180°.其中是随机事件的是________(只填写序号即可).
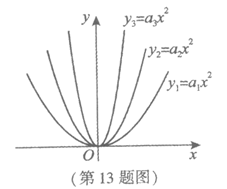
13.在同一个平面直角坐标系xOy中,二次函数y1=a1x2,y2=a2x2,y3=a3x2的图象如图所示,则a1,a2,a3的大小关系为________.
14.响应国家号召打赢脱贫攻坚战,小明利用信息技术开了一家网络商店,将家乡的土特产销往全国,今年6月份盈利24000元,8月份盈利34560元,求6月份到8月份盈利的月平均增长率,设6月份到8月份盈利的月平均增长率为x,根据题意,可列方程为____________.
15.如图,在平面直角坐标系xOy中,等边△ABC的顶点A在y轴的正半轴上,B(-5,0),C(5,0),点D(11,0),将△ACD绕点A顺时针旋转60°得到△ABE,则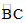 的长度为____,线段AE的长为____,图中阴影部分面积为________.
的长度为____,线段AE的长为____,图中阴影部分面积为________.
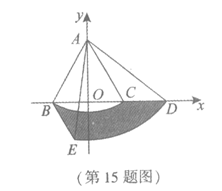
16.不透明的盒子中装有红、黄色的小球共20个,除颜色外无其他差别,随机摸出一个小球,记录颜色后放回并摇匀,再随机摸出一个,下图显示了某数学小组开展上述摸球活动的某次实验的结果.
下面有四个推断:
①当摸球次数是300时,记录“摸到红球“的次数是99,所以“摸到红球“的概率是0.33;
②随着试验次数的增加,“摸到红球“的频率总在0.35附近摆动,显示出一定的稳定性,可以估计“摸到红球“的概率是0.35;
③可以根据本次实验结果,计算出盒子中约有红球7个;
④若再次开展上述摸球活动,则当摸球次数为500时,“摸到红球“的频率一定是0.40.
所有合理推断的序号是________.
三、解答题(本题共31分,第17-20题,每小题5分,第21题6分,第22题5分)
17.关于x的一元二次方程x2+(2m-1)x+m2+m-2=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为正整数,写出一个符合条件的m的值并求出此时方程的根.
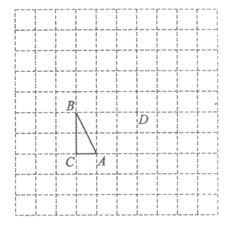
18.如图,在边长为1个单位长度的小正方形组成的网格中,给出了△ABC和点D(A,B,C,D是网格线交点).
(1)画出一个△DEF,使它与△ABC全等,且点D与点A是对应点,点E与点B是对应点,点F与点C是对应点(要求:△DEF是由△ABC经历平移、旋转得到的,两种图形变化至少各一次).
(2)在(1)的条件下,在网格中建立平面直角坐标系,写出点C和点F的坐标.
19.已知:如图,△ABC中,∠C= 90°.
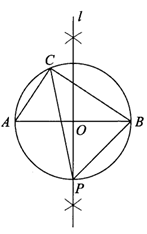
求作:∠CPB=∠A,使得顶点P在AB的垂直平分线上。
作法:①作AB的垂直平分线l,交AB于点O;
②以O为圆心,OA为半径画圆,⊙O与直线l的一个交点为P(点P与点C在AB的两侧);
③连接BP,CP.
∠CPB就是所求作的角.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明。
证明:连接OC,
∵l为AB的垂直平分线,
∴OA=_________.
∵∠ACB=90°.
∴OA=OB=OC.
∴点A,B,C都在⊙O上,
又∵点P在⊙O上,
∴∠CPB=∠A(______________)(填推理依据).
20.12月4日是全国法制宣传日.下面是某校九年级四个班的学生(各班人数相同)在一次“宪法知识竞答“活动中的成绩的频数分布表:
班级 | 70≤x<75 | 75≤x<80 | 80≤x<85 | 85≤x<90 | 90≤x<95 | 95≤x≤100 |
一班 | 2 | 0 | 3 | 7 | 8 | 0 |
二班 | 0 | 1 | 5 | 7 | 7 | 0 |
三班 | 0 | 1 | 4 | 7 | 7 | 1 |
四班 | m | 0 | 3 | 7 | 5 | 2 |
(1)频数分布表中,m=____,
(2)从70≤x<75中,随机抽取2名学生,那么所抽取的学生中,至少有1人是一班学生的概率是多少?
21.如图,AB为⊙O的直径,C为⊙O上一点,D是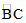 的中点,过点D作AC的垂线,交AC的延长线于点E,连接AD.
的中点,过点D作AC的垂线,交AC的延长线于点E,连接AD.
(1)求证:DE是⊙O的切线;
(2)连接CD,若∠CDA=30°,AC=2,求CE的长.
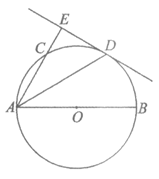
22.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-3与直线y=-x-1交于点A(-1,0),B(m,-3),点P是线段AB上的动点.
(1)①m=____________;
②求抛物线的解析式.
(2)过点P作直线l垂直于x轴,交抛物线y=ax2+bx-3于点Q,求线段PQ的长最大时,点P的坐标.
四、解答题(本题共21分,每小题7分)
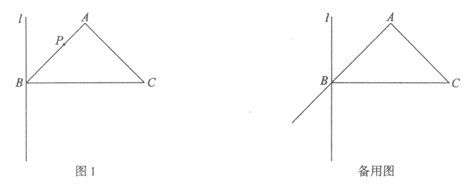
23.在等腰直角△ABC中,AB=AC,∠A=90°,过点B作BC的垂线l.点P为直线AB上的一个动点(不与点A,B重合),将射线PC绕点P顺时针旋转90°交直线l于点D.
(1)如图1,点P在线段AB上,依题意补全图形.
①求证:∠BDP=∠PCB;
②用等式表示线段BC,BD,BP之间的数量关系,并证明.
(2)点P在线段AB的延长线上,直接写出线段BC,BD,BP之间的数量关系.
24.已知抛物线y=ax2+2ax+3a2-4.
(1)该抛物线的对称轴为____________,
(2)若该抛物线的顶点在x轴上,求抛物线的解析式;
(3)设点M(m,y1),N(2,y2)在该抛物线上,若y1>y2,求m的取值范围.
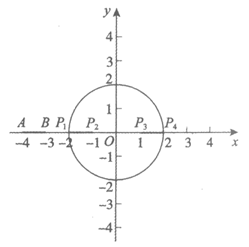
25.在平面直角坐标系xOy中,⊙O的半径为2,A,B为⊙O外两点,AB=1,给出如下定义:
平移线段AB,使线段AB的一个端点落在⊙O上,其他部分不在⊙O外,点A,B的对应点分别为点A’,B’,线段AA’长度的最大值称为线段AB到⊙O的“极大距离“,记为d(AB,⊙O).
(1)若点A(-4,0).
①当点B为(-3,0),如图所示,平移线段AB,在点P1(-2,0),P2(-1,0),P3 (1,0),P4(2,0)中,连接点A与点________的线段的长度就是d(AB,⊙O);
②当点B为(-4,1),求线段AB到⊙O的“极大距离“所对应的点A’的坐标.
(2)若点A(-4,4),d(AB,⊙O)的取值范围是________________.
参考答案
一、选择题(本题共24分.每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | A | C | C | C | D | B | B | A |
二、填空题(本题共24分.每小题3分)
题号 | 9 | 10 | 11 | 12 |
答案 | 1.5 | 90°-α |
| ② |
题号 | 13 | 14 | 15 | 16 |
答案 | a1<a2<a3 | 24000 (1 +x)2=34560 |
| ②③ |
三、解答题(本题共31分,第17-21题,每小题5分,第21题6分,第22题5分)
17. 解:(1)由题意,△=(2m-1)2-4(m2+m-2)>0 …………………………1分
解得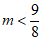 …………………………………………………2分
…………………………………………………2分
(2)m=1 ……………………………………3分
此时方程为x2+x=0
∴方程的根为x1=0,x2=-1……………………………5分
18. 解:答案不唯一,如:
(1)
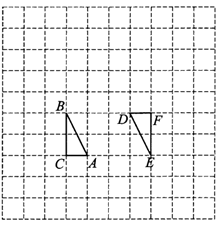 …………3分
…………3分
(2) C(0,0),F(4,2)……………………5分
19.解:(1)
 …………………3分
…………………3分
(2)OB ……………………………………………………4分
同弧所对的圆周角相等 ……………………………………5分
20.解:(1)3……………………………………………………1分
(2)一班有2人,分别记为A,B;四班有3人,分别记为C,D,E
随机抽取2人的情况有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE ………4分
至少有1人是一班学生的情况有AB,AC,AD,AE,BC,BD,BE.
所以至少有1人是一班学生的概率是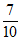 . …………………………………………5分
. …………………………………………5分
21.(1)证明:如图1.连接OD,
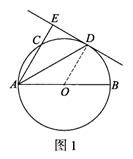
∵D是 的中点.
的中点.
∴∠BAD=∠CAD. ………………………………………1分
∵OA=OD,
∴∠BAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AE.…………………………………2舟
∵DE⊥AC,
∴ DE⊥OD
∴ DE是⊙O的切线…………………………………………3分
(2)解:如图2,连接OC,
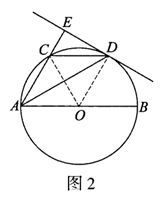
∵∠CDA=30°,
∴∠AOC=3∠CDA=60°.……………………………………4分
∴△AOC是等边三角形
∴由(1)可得,四边形ACDO是菱形.
∴CD=AC=2,∠CDE=30°.……………………………… 5分
∴CE=1.…………………………………………6分
22.解:(1)①2.……………………………………1分
②由①得,点B(2,-3)
∵点A(-1,0),B(2,-3)在抛物线y=ax2+bx-3上,
∴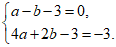 ……………………………………2分
……………………………………2分
解得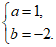
∴抛物线的解析式为y=x2-2x-3 ……………………………………3分
(2)设点P的横坐标为x,其中-1≤x≤2.
∴点P(x,-x-1),点Q(x,x2-2x-3)
∴PQ=-x2+x+2.……………………………………4分
∴当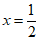 时,PQ最大
时,PQ最大
此时点P的坐标是(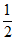 ,
,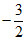 )…………………………………5分
)…………………………………5分
四、解答题(本题共21分,每小题7分)
23.解:(1)补全图形,如图
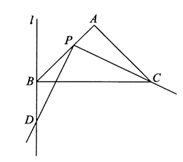 …………………………2分
…………………………2分
①证明:如图①,设PD与BC的交点为E.
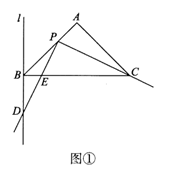
根据题意可知,∠CPD= 90°
∵BC⊥l,
∴∠DBC=90°.
∴∠BDP+∠BED=∠PCB+∠PEC=90°
∴∠BDP=∠PCB. ……………………………………3分
②BC-BD=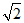 BP………………………………4分
BP………………………………4分
证明:如图②,过点P作PF⊥BP交BC于点F.
∵AB=AC,∠A=90°
∴∠ABC=45°.
∴BP=PF. ∠PFB=45°.
∴∠PBD=∠PFC=135°.………………5分
∴△BPD≌△FPC.………………………………6分
∴BD= FC.
∵BF=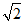 BP,
BP,
∴BC-BD= BP.
BP.
(2)BD-BC=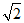 BP.……………………………………7分
BP.……………………………………7分
24.解:(1)直线x=-1………………………………1分
(2)∵抛物线顶点在x轴上
∴顶点坐标为(-1,0).
解得a=-1或
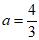 ……………………………………3分
……………………………………3分
∴抛物线解析式为y=-x2-2x-1或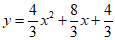 ………………………………4分
………………………………4分
(3)∵抛物线的对称轴为直线x=-1,
∴N(2,y2)关于直线x=-1的对称点为N'( -4,y2)……………………………5分
(i)当a>0时,若y1>y2,则m<-4或m>2;…………………………………………6分
(ii)当a<0时,若y1>y2,则-4<m<2 ………………………………………7分
25.解:(1)①P3.………………………………………2分
②如图,A’B’⊥x轴于点M.
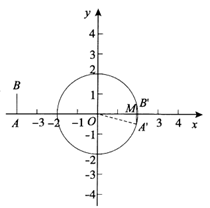
∴M为A’B’中点.
∴A’M=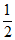
∴
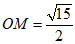 .
.
∴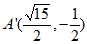 …………………………4分
…………………………4分
(2) 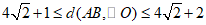 …………………7分
…………………7分



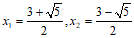
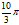 ,14,16π
,14,16π