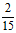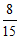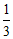本试卷满分共150分
考试时间120分钟
第一部分
(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合A={x|-2<x≤1},B={x|0<x≤3},则A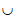 B=
B=
(A){x|-2<x<0} (B){x|0 <x≤1}
(C){x|1<x≤3} (D){x|-2<x≤3}
(2)在复平面内,复数z=3-4i,则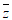 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
(3)已知双曲线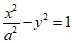 (a>0)的离心率是
(a>0)的离心率是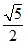 ,则a=
,则a=
(A)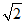 (B)2
(B)2
(C)
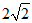 (D)4
(D)4
(4)在平面直角坐标系xOy中,角α以Ox为始边,且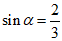 ,把角α的终边绕端点O逆时针方向旋转π弧度,这时终边对应的角是β,则sinβ=
,把角α的终边绕端点O逆时针方向旋转π弧度,这时终边对应的角是β,则sinβ=
(A)
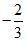 (B)
(B)
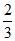
(C)
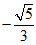 (D)
(D)
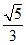
(5)若直线y=kx+1是圆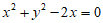 的一条对称轴,则k的值为
的一条对称轴,则k的值为
(A)
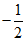 (B)-1
(B)-1
(C)1 (D)2
(6)某三棱锥的三视图如图所示,则该三棱锥中最长的棱长为
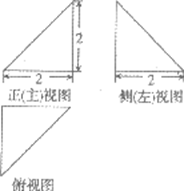
(A)2
(B)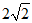
(C)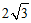
(D)4
(7)P为抛物线y2=2px(p>0)上一点,点P到抛物线准线和对称轴的距离分别为10和6,则p=
(A)2 (B)4
(C)4或9 (D)2或18
(8)大气压强 ,它的单位是“帕斯卡“(Pa,1Pa=1N/m2),大气压强p(Pa)随海拔高度h(m)的变化规律是p=p0e-kh(k=0.000126 m-1),p0是海平面大气压强.已知在某高山A1,A2两处测得的大气压强分别为p1, p2,
,它的单位是“帕斯卡“(Pa,1Pa=1N/m2),大气压强p(Pa)随海拔高度h(m)的变化规律是p=p0e-kh(k=0.000126 m-1),p0是海平面大气压强.已知在某高山A1,A2两处测得的大气压强分别为p1, p2,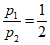 ,那么A1,A2两处的海拔高度的差约为(参考数据:ln2≈0.693)
,那么A1,A2两处的海拔高度的差约为(参考数据:ln2≈0.693)
(A)550 m (B)1818 m
(C)5500 m (D) 8732 m
(9)已知非零向量a,b,c共面,那么“存在实数λ,使得a=λc成立“是“(a·b)c=a(b·c)”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(10)已知函数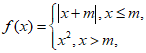 若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则实数m的取值范围是
若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则实数m的取值范围是
(A)(0,2) (B)(-∞,-2)
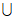 (0,2)
(0,2)
(C)(-2,0) (D)(-2,0)
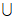 (2,+∞)
(2,+∞)
第二部分
(非选择题
共110分)
二、填空题共5小题,每小题5分,共25分。
(11)函数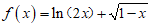 的定义域为________.
的定义域为________.
(12)在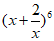 的展开式中,常数项为________.(用数字作答)
的展开式中,常数项为________.(用数字作答)
(13)在△ABC中,a=
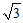 ,b =
,b =
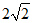 ,B=2A,则cosA=________.
,B=2A,则cosA=________.
(14)设等比数列{an}满足a1+a2=48,a4+a5=6,则1og2(a1a2a3…an)的最大值为________.
(15)如图,从长、宽、高分别为a,b,c的长方体AEBF-GCHD中截去部分几何体后,所得几何体为三棱锥A-BCD.下列四个结论中,所有正确结论的序号是________.
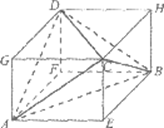
①三棱锥A-BCD的体积为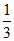 abc;
abc;
②三棱锥A-BCD的每个面都是锐角三角形;
③三棱锥A-BCD中,二面角A-CD-B不会是直二面角;
④三棱锥A-BCD中,三条侧棱与底面所成的角分别记为α,β,γ,则sin2α+sin2β+ sin2γ≤2.
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题13分)
已知函数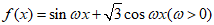 .
.
(I)当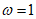 时,求
时,求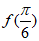 的值;
的值;
(Ⅱ)当函数f(x)图象的两条相邻对称轴之间的距离是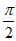 时,__________.
时,__________.
从①②③中任选一个,补充到上面空格处并作答.
①求f(x)在区间[0,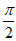 ]上的最小值;
]上的最小值;
②求f(x)的单调递增区间;
③若f(x)≥0,求x的取值范围.
注:如果选择多个问题分别解答,按第一个解答计分。
(17)(本小题14分)
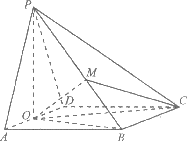
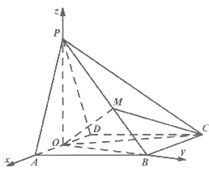
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=
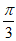 ,M是棱PB上的点,O是AD中点,且PO⊥底面ABCD,OP=
,M是棱PB上的点,O是AD中点,且PO⊥底面ABCD,OP=
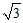 OA.
OA.
(I)求证:BC⊥OM;
(Ⅱ)若PM=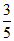 PB,求二面角B-OM-C的余弦值.
PB,求二面角B-OM-C的余弦值.
(18)(本小题14分)
某电影制片厂从2011年至2020年生产的科教影片、动画影片、纪录影片的时长(单位:分钟)如下图所示.
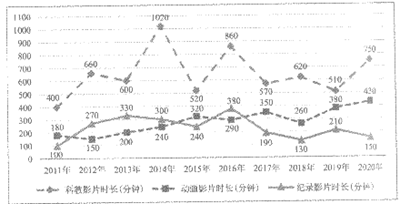
(I)从2011年至2020年中任选一年,求此年动画影片时长大于纪录影片时长的概率;
(Ⅱ)从2011年至2020年中任选两年,设X为选出的两年中动画影片时长大于纪录影片时长的年数,求X的分布列和数学期望E(X);
(Ⅲ)将2011年至2020年生产的科教影片、动画影片、纪录影片时长的方差分别记为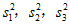 ,试比较
,试比较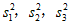 的大小.(只需写出结论)
的大小.(只需写出结论)
(19)(本小题15分)
已知椭圆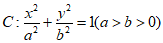 长轴的两个端点分别为A(-2,0),B(2,0),离心率为
长轴的两个端点分别为A(-2,0),B(2,0),离心率为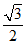 .
.
(I)求椭圆C的方程;
(Ⅱ)P为椭圆C上异于A,B的动点,直线AP,PB分别交直线x=-6于M,N两点,连接NA并延长交椭圆C于点Q.
(i)求证:直线AP,AN的斜率之积为定值;
(ii)判断M,B,Q三点是否共线,并说明理由.
(20)(本小题15分)
已知函数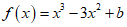 (b∈R).
(b∈R).
(I)当b=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若函数f(x)存在三个零点,分别记为x1,x2,x3(x1<x2<x3).
(i)求b的取值范围;
(ii)证明:x1+x2>0.
(21)(本小题14分)
已知数列A:a1,a2,…,a2n(n∈N*),现将数列A的项分成个数相同的两组,第一组为B:b1,b2,…,bn,满足bi≥bi+1(i=1,2,…,n-1);第二组为C:c1,c2,…,cn,满足ci≤ci+1(i=1,2,…,n-1),记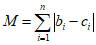 .
.
(I)若数列A:1,2,4,8,写出数列A的一种分组结果,并求出此时M的值;
(Ⅱ)若数列A:1,2,3,…,2n,,证明:max{bi,ci}≥n+1(i=1,2,…,n);(其中max{bi,ci}表示bi,ci中较大的数)
(Ⅲ)证明:M的值与数列A的分组方式无关.
参考答案
一、选择题(共10小题,每小题4分,共40分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | A | B | A | B | C | D | C | C | B |
二、填空题(共5小题,每小题5分,共25分)
11.(0,1] 12. 160 13.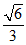
14. 15 15.①②④
三、解答题(共6小题,共85分)
(16)(本小题13分)
解:(I)当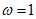 时,
时,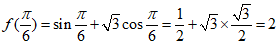 ……………5分
……………5分
(II)
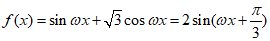
因为函数f(x)图象的两条相邻对称轴之间的距离是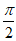 ,
,
所以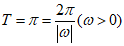 ,解得
,解得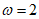 .
.
所以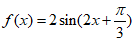 . ………………9分
. ………………9分
选①:因为0≤x≤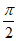 ,所以
,所以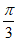 ≤2x+
≤2x+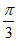 ≤
≤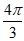 .
.
当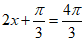 ,即
,即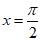 时,
时,
f(x)在区间[0,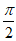 ] 上有最小值为
] 上有最小值为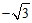 . ……………………13分
. ……………………13分
选②:令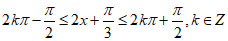 ,
,
解得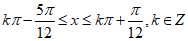 ,
,
所以函数f(x)的单调递增区间为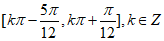 .
.
选③:因为f(x)≥0,所以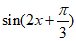 .
.
所以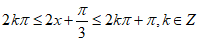
解得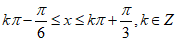
(17)(本小题14分)
(I)证明:在菱形ABCD中,∠BAD=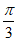 ,△ABD为等边三角形.
,△ABD为等边三角形.
因为O为AD的中点,
所以OB⊥AD.
因为AD∥BC,
所以OB⊥BC.
因为PO⊥底面ABCD,BC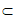 平面ABCD,
平面ABCD,
所以OP⊥BC.
因为OP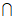 OB=O,OP,OB
OB=O,OP,OB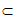 平面POB,
平面POB,
所以BC⊥平面POB.
因为M是棱PB上的点,
所以OM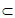 平面POB.
平面POB.
所以BC⊥OM.……………………6分
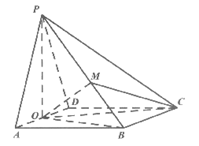
(II)解:因为PO⊥底面ABCD,OB⊥AD,
建立如图所示空间直角坐标系O-xyz,设OA=1,则OP=OB=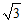 .
.
因为O(0,0,0),A(1,0,0),B(0,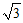 ,0),C(-2,
,0),C(-2,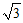 ,0),P(0,0,
,0),P(0,0,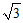 ),
),
所以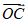 = (-2,
= (-2,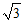 ,0).
,0).
由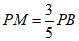 ,
,
得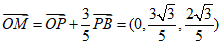 .
.
设m=(x,y,z)是平面OMC的法向量,
由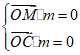 ,得
,得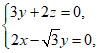 ,
,
令y=2,则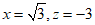 ,则
,则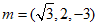 .
.
又因为平面POB的法向量为n=(1,0,0),……10分
所以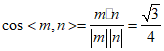 .…12分
.…12分
由题知,二面角B-OM-C为锐二面角,
所以二面角B-OM-C的余弦值为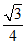 ,………14分
,………14分
(18)(本小题14分)
解:(I)从2011年至2020年中任选一年,动画影片时长大于纪录影片时长的年份分别是2011年,2015年,2017年,2018年,2019年和2020年,共6年.
记从2011年至2020年中任选一年,此年动画影片时长大于纪录影片时长为事件A,
则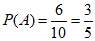 ……………………4分
……………………4分
(II)X的所有可能取值为0,1,2.
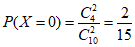 ;
;
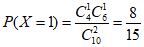 ;
;
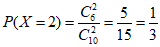 .
.
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
数学期望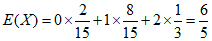 ……………………12分
……………………12分
(III)
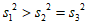 .…………………………14分
.…………………………14分
(19)(本小题15分)
解:(I)由题意a=2,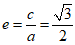 ,所以
,所以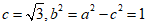 .
.
所以椭圆C的方程为
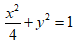 .………………………4分
.………………………4分
(II)(i)证明:设P(x0,y0),
因为P在椭圆C上,所以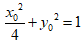 .
.
因为直线AP的斜率为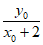
,直线BP的斜率为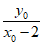 ,
,
所以直线BP的方程为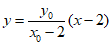 .
.
所以N点的坐标为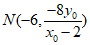 .
.
所以直线AN的斜率为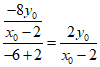 .
.
所以直线AP,AN的斜率之积为
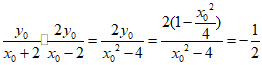 ………………………9分
………………………9分
(ii)M,B,Q三点共线,
设直线AP斜率为k,易得M(-6,-4k).
由(i)可知直线AN斜率为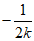 ,所以直线AN的方程为
,所以直线AN的方程为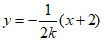 .
.
联立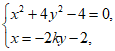 可得
可得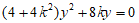 .
.
解得Q点的纵坐标为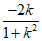 ,所以Q点的坐标为Q
,所以Q点的坐标为Q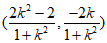 .
.
所以,直线BQ的斜率为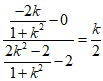 ,直线BM的斜率为
,直线BM的斜率为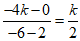 .
.
因为直线BQ的斜率等于直线BM的斜率,
所以M,B,Q三点共线. ………15分
(20)(本小题15分)
解:(I)当b=1时,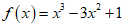 ,得
,得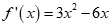 ,
,
因为f(1)= -1,f'(1)=-3,
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-(-1)=-3(x-1),即3x+y-2=0.…………………1分
(II)因为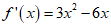 ,
,
所以令f'(x)=0,得x=0,x=2.
f'(x),f(x)随x的变化如下:
x | (-∞,0) | 0 | (0,2) | 2 | (2,+∞) |
f'(x) | + | 0 | – | 0 | + |
f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
所以f(x)的极大值为f(0)=b,极小值为f(2)=b-4. ……………7分
(i)若函数f(x)存在三个零点,分别记为x1,x2,x3 (x1<x2<x3),
则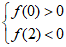 ,所以0<b<4. ………………10分
,所以0<b<4. ………………10分
当0<b<4时,f(-1)=b-4<0,f(3)=b>0,
此时f(-1)·f(0)<0,f (0) ·f(2)<0,f(2)·f(3)<0,故f(x)存在三个零点,
所以若函数f(x)存在三个零点,b的取值范围是0<b<4. ………………12分
(ii)证明:因为x1,x2,x3 (x1<x2<x3)是函数f(x)的零点,
所以x1<0<x2<x3.
因为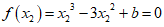 ,
,
所以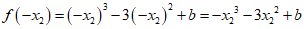
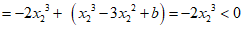 .
.
因为f(x1) =0,所以f(-x2)<f(x1).
又因为x1,-x2∈(-∞,0),且f(x)在区间(-∞,0)上单调递增,
所以-x2<x1,即x1+x2>0. ………………15分
(21)(本小题14分)
解:( I)可将数列A分成:B:8,4;C:1,2.此时M=|8-1|+|4-2|=9. …………3分
(II)因为bi≥bi+1,ci≤ci+1(i=1,2,L,n-1),
所以max {bi,ci}≥bi≥bi+i≥bi+2≥L≥bn(i=1,2,L,n),
max{bi,ci)≥ci≥ci-1≥ci-2≥L≥c1.
所以max {bi,ci}≥max{bi,bi+1,bi+2,L,bn,ci,ci-1, ci-2,L,c1}.
因为bi,bi+1, bi+2,L,bn,ci,ci-1, ci-2,L,c1共n+1项,
所以max{bi,bi+1,bi+2,L,bn,ci,ci-1, ci-2,L,c1}≥n+1.
所以max{bi,ci}≥n+1. ……………9分
(III)不妨将数列A:a1,a2,L,a2n(n∈N*)重新排序得到
数列A’: a1‘,a2 ‘,L,a2n'(n∈N*),满足ai‘≤ai+1‘(i=1,2,L,2n-1).
因为bi≥bi+1,ci≤ci+1(i=1,2,L,n-1),
所以max{bi,ci}≥bi≥bi+1≥bi+2≥L≥bn(i=1,2,L,n),
max{bi,ci}≥ci≥ci-1≥ci-2≥L≥c1
所以max{bi,ci}≥max{bi, bi+1, bi+2,L,bn,ci,ci-1, ci-2,L,ci}.
因为bi,bi+1, bi+2,L,bn,ci,ci-1, ci-2,L,c1共n+1项,
所以max{bi,ci}恰为an+i‘,an+2‘,L,a2n‘(n∈N*)中某一项.
同理min{bi,ci}恰为a1‘,a2‘,L,an‘(n∈N*)中某一项(其中min{bi,ci}表示bi,ci中较小的数).
因为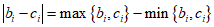 ,
,
所以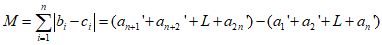 .
.
所以M的值与数列A的分组方式无关, ………………14分
(若用其他方法解题,请酌情给分)