北京101中学2022届上学期初中九年级9月开学数学试卷
考试时间:120分钟
满分:100分
一、选择题:本大题共16分,每题2分。
1. 备受关注的北京环球度假区宣布将于2021年9月1日正式开启试运行。根据规划,北京环球影城建成后一期预计年接待游客超过1000万人次,将1000万用科学记数法表示为
A. 0. 1×104 B. 1. 0×103 C. 1. 0×106 D. 1. 0×107
2. 实数m,n在数轴上的对应点如图所示,则下列各式子正确的是

A. -m>|n| B. -n>|m| C. m>n D. |m|<|n|
3. 已知正多边形的一个外角为36°,则该正多边形的边数为
A. 12 B. 10 C. 8 D. 6
4. 函数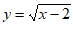 的自变量x的取值范围是
的自变量x的取值范围是
A. x>2 B. x<2 C. x≤2 D. x≥2
5. 如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠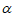 =135°,则∠
=135°,则∠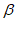 等于
等于
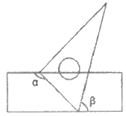
A. 75° B. 60° C. 45° D. 85°
6. 已知锐角∠AOB,如图,
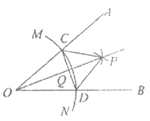
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧MN,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;
(3)作射线OP交CD于点Q。
根据以上作图过程及所作图形,下列结论中错误的是
A. ∠AOP=∠BOP B. CP=2QC
C. CP∥OB D. CD⊥OP
7. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载。如图1,以直角三角形的各边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内。则图中阴影部分的面积等于
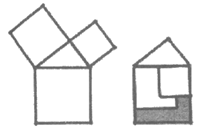
A. 直角三角形的面积
B. 最大正方形的面积
C. 较小两个正方形重叠部分的面积
D. 最大正方形与直角三角形的面积和
8. 如图,是一对变量满足的函数关系的图象。有下列3个不同的问题情境:
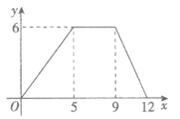
①小明骑车以400m/min的速度匀速骑了5min,在原地休息了4min,然后以500m/min的速度匀速骑回出发地,设时间为x min,离出发地的距离为y km;
②有一个容积为6L的开口空桶,小亮以1.2 L/min的速度匀速向这个空桶注水,注5 min后停止,等4 min后,再以2 L/min的速度匀速倒空桶中的水,设时间为x min,桶内的水量为y L;
③矩形ABCD中,AB=4,BC=3,动点P从点A出发,依次沿对角线AC,边CD,边DA运动至点A停止,设点P的运动路程为x,当点P与点A不重合时,y=S△ABP;当点P与点A重合时,y=0。
其中,符合图中所示函数关系的问题情境为
A. ② B. ②③ C. ①③ D. ①②
二、填空题:本大题共16分,每题2分。
9. 已知x=2y+3,则代数式4x-8y+9的值是________________。
10. 分解因式4ax2-4ax+a=________________。
11. 把直线l1:y=2x-1向上平移3个单位后,得到的新直线l2与×轴的交点坐标为________________。
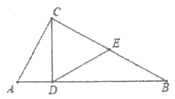
12. 如图,在Rt△ABC中,∠ACB=90°,∠A=62°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠EDC的度数是________________。
13. 如图,直线y=kx+b(k<0)经过点A(3,1),当kx+b<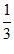 x时,x的取值范围为________。
x时,x的取值范围为________。
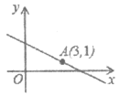
14. 如图,正方形ABCD对角线交于点O,CP⊥DP于点P,CP=5,DP=7,则△POD的面积为________。
15. 如图,在甲,乙两个十字路口各方向均设有人行横道和交通信号灯,小宇在甲路口西南角的A处,需要步行到对于乙路口东北角B处附近的餐馆用餐,已知两路口人行横道交通信号灯的切换时间与小宇的步行时间如下表所示:
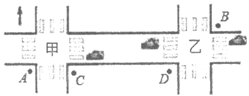 (图中箭头↑所示方向为北)
(图中箭头↑所示方向为北)
人行横道交通信号灯的切换时间 | 小宇的步行时间 | ||
甲路口 | 每1 min | 沿人行横道穿过一条马路 | 0. 5min |
乙路口 | 每2 min | 在甲、乙两路口之间(CD段) | 6 min |
假定人行横道的交通信号灯只有红、绿两种,且在任意时刻,同一十字路口东西向和南北向的交通信号灯颜色不同,行人步行转弯的时间可以忽略不计,若小宇在A处时,甲、乙两路口人行横道东西向的交通信号灯均恰好转为红灯,小宇从A处到达B处所用的最短时间为_______________min。
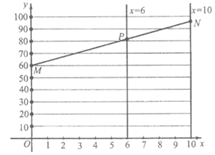
16. 为了迅速算出学生的学期总评成绩,一位同学创造了一张奇妙的算图。如图,y轴上动点M的纵坐标ym表示学生的期中考试成绩,直线x=10上动点N的纵坐标yn表示学生的期末考试成绩,线段MN与直线x=6的交点为P,则点P的纵坐标yP就是这名学生的学期总评成绩。有下面几种说法:①若某学生的期中考试成绩为70分,期末考试成绩为80分,则他的学期总评成绩为75分;②甲同学的期中考试成绩比乙同学高10分,但期末考试成绩比乙同学低10分,那么甲的学期总评成绩比乙同学低;③期中成绩占学期总评成绩的60%。结合这张算图进行判断,其中正确的说法是___________。(填写序号)
三、解答题:本题共68分,第17-21题,每小题5分,第22-24,每小题6分,25题5分,第26-27题,每小题7分,第28题6分。
17. 计算: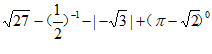
18. 解不等式组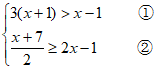 。
。
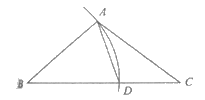
19. 如图,在△ABC中,以点B为圆心,BA长为半径画弧,交BC边于点D,连接AD。若∠B=40°,∠C=32°,求∠DAC的度数。
20. 先阅读下列材料,再解答问题。
尺规作图:
已知:△ABC,D是边AB上一点,如图1,
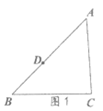
求作:四边形DBCF,使得四边形DBCF是平行四边形。
小明的做法如下:
(1)设计方案 |
先画一个符合题意的草图,如图2, 再分析实现目标的具体方法,
|
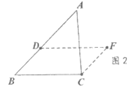
(2)设计作图步骤,完成作图 |
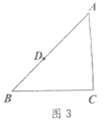
作法:如图3, ①以点C为圆心、BD为半径画弧; ②再以点D为圆心、BC为半径画弧,两弧交于点F; ③连接DF与CF。 ∴四边形DBCF即为所求。 请在图3中完成尺规作图,保留作图痕迹
|
(3)推理论证 |
证明:∵__________,__________ ∴四边形DBCF是平行四边形。(____________________)(填推理依据) |
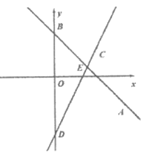
21. 如图,在平面直角坐标系中,直线y=-x+3过点A(5,m),且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C。过点C且与y=2x平行的直线交y轴于点D。
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,请直接写出,直线CD在平移过程中与x轴交点的横坐标x0的取值范围。
22. 已知关于x的一元二次方程x2–(k+5)x+3k+6=0。
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于-2且小于0,k为整数,求k的值。
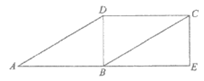
23. 如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE。
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长。
24. “绿水青山就是金山银山“,某社区响应号召,开展“青山绿水“行动,计划对面积为3600m2的区域进行绿化,经投标由甲、乙两个工程队来完成。已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为600m2区域的绿化时,甲队比乙队少用6天。
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
25. 教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果。现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息。
a. 教育未来指数得分的频数分布直方图(数据分成7组:20≤x<30,30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x≤90);
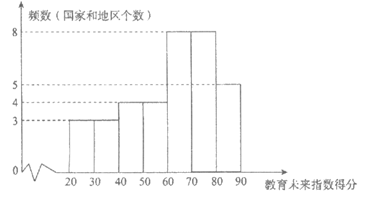
b. 未来教育指数得分在60≤x<70这一组的是:
61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
c. 35个国家的人均国内生产总值和教育未来指数得分情况统计图
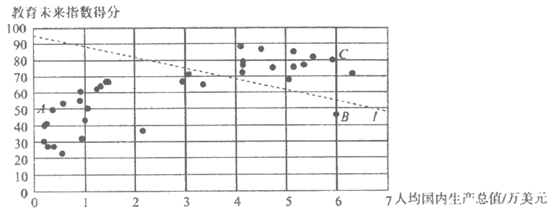
d. 中国和中国香港的未来教育指数得分分别为32.9和68.5。
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)中国香港的教育未来指数得分排名世界第_________;
(2)在35个国家和地区的人均国内生产总值和国家教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○“画出代表中国香港的点;
(3)在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为_______万美元;(结果保留一位小数)
(4)下列推断合理的是__________。(只填序号即可)
①相比于点A,C所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五“规划提出“教育优先发展,教育强则国家强“的任务,进一步提高国家教育水平;
②相比于点B,C所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全国建成小康社会“的奋斗目标,进一步提高人均国内生产总值。
26. 定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足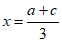 ,
,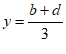 ,那么称点T是点A,B的“相似点“。
,那么称点T是点A,B的“相似点“。
例如:A(-1,8),B(4,-2),当T(x,y)满足x=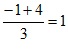 ,
,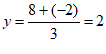 时,则点T(1,2)是点A,B的“相似点“。
时,则点T(1,2)是点A,B的“相似点“。
(1)已知点A(-1,5),B(7,7),C(2,4),请说明其中一个点是另外两个点的“相似点“。
(2)如图,点D(3,0)在x轴上,点E(t,2t+3)是直线l上任意一点,点T(x,y)是点D,E的“相似点“。
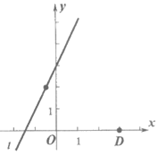
①试确定y与x的关系式。
②若直线ET交x轴于点H,当△DTH为直角三角形时,请直接写出点E的坐标。
27. 在△ABC中,∠A=90°,AB=AC。
(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“QB=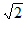 QA”是否正确:_________(填“是“或“否“);
QA”是否正确:_________(填“是“或“否“);
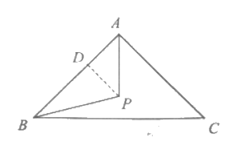
(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB= PA。
PA。
①如图2,点P在△ABC内,∠ABP=30°;求∠PAB的大小;
②如图3,点P在△ABC外,连接PC,设∠APC=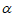 ,∠BPC=
,∠BPC=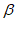 ,求
,求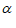 +
+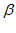 的值。
的值。

图1 图2 图3
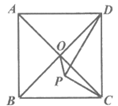
28. 在平面直角坐标系xOy中,如果点A、点C为某个菱形的一组对角的顶点,且点A、C在直线y=x上,那么称该菱形为点A、C的“最佳菱形“。下图为点A、C的“最佳菱形“的一个示意图。已知点M的坐标为(1,1),点P的坐标为(3,3)。
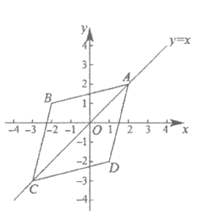
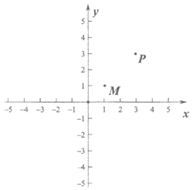
(1)点E(1,3),F(2,1),G(4,0)中,能够成为点M、P的“最佳菱形“的顶点的是____________;
(2)如果四边形MNPQ是点M、P的“最佳菱形“。
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;
②当四边形MNPQ的面积为8,且与直线y=x+b有公共点时,直接写出b的取值范围。
参考答案
(考试时间:120分钟
满分:100分)
一、选择题:本大题共16分,每题2分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | A | B | D | A | C | C | B |
二、填空题:本大题共16分,每题2分。
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 | 21 |
| (-1,0) | 62° |
| 3.5 | 8 | ② |
三、解答题:本题共68分,第17-21题,每小题5分,第22-24,每小题6分,25题5分,第26-27题,每小题7分,第28题6分。
17. 解:原式=3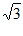 -2-
-2-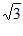 +1 …4分
+1 …4分
=2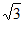 -1 …5分
-1 …5分
18. 解:解①得x>-2…………2分
解②得x≤3………4分
原不等式解集为-2<x≤3…………5分。
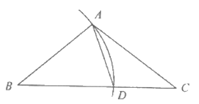
19. 解:∵AB=DB,∠B=40°
∴∠BAD=∠BDA=70°
∵∠BDA=∠DAC+∠C,∠C=32°………3分
∴∠DAC=70°-32°=38°……5分
20. (2)如图。……………2分
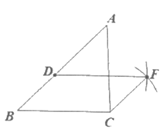
(3)证明:
∵CF=BD,DF=BC,……4分。
∴四边形DBCF是平行四边形(两组对边分别相等的四边形是平行四边形)。…5分
21. 解:(1)A(5,-2),C(3,2),直线CD解析式为y=2x-4………3分;
(2)–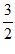 ≤x0≤2。……5分
≤x0≤2。……5分
22. (1)证明:依题意,得△=[–(k+5)]2-4(3k+6)…1分
=k2-2k+1=(k-1)2…2分
∵(k-1)2≥0,∴此方程总有两个实数根。…3分
(2)解:解方程得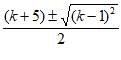 …4分
…4分
∴方程的两个根为x1=k+2,x2=3. …5分
由题意可知,-2<k+2<0,即-4<k<-2。
∵k为整数,
∴k=-3。…6分
23. (1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB。…1分
∵BE=AB,
∴BE=CD。
∴四边形BECD是平行四边形。…2分
∵∠ABD=90°,
∴∠DBE=90°。
∴□BECD是矩形。…3分
(2)解:如图,取BE中点G,连接FG。
由(1)可知,FB=FC=FE,
∴FG=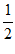 CE=1,FG⊥BE. …4分
CE=1,FG⊥BE. …4分
∵在□ABCD中,AD∥BC,
∴∠CBE=∠DAB=30°。
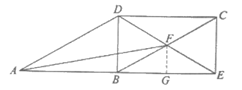
∴BG=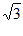 。
。
∴AB=BE=2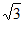 。
。
∴AG=3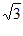 …5分
…5分
∴在Rt△AGF中,由勾股定理可求AF=2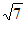 。…6分
。…6分
24. 解:(1)设乙队每天能完成的绿化面积为xm2,则甲队每天能完成的绿化面积为2xm2,根据题意,得: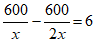 ,………1分
,………1分
解得:x=50,经检验,x=50是原方程的解,…………2分
∴2x=100。
答:甲队每天能完成的绿化面积为100m2,乙队每天能完成的绿化面积为50m2. 3分
(2)设甲工程队施工a天,乙工程队施工b天刚好完成绿化任务。
由题意得: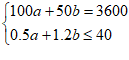 ,…4分
,…4分
解得a≥32
答:至少应安排乙工程队绿化32天。……6分
25. 解:(1)14………1分
(2)略………2分
(3)6.3……………3分
(4)①②…5分
26. 解:(1)∵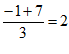 ,
,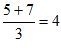 ,
,
∴点C(2,4)是点A、B的相似点。………2分
(2)①由相似点定义知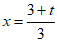 ,得t=3x-3………………3分
,得t=3x-3………………3分
又∵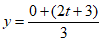 ,得t=
,得t=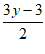 …4分
…4分
∴3x-3=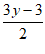 ,化简得y=2x-1 …5分
,化简得y=2x-1 …5分
②符合题意的点为E1(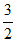 ,6),E2(6,15)。…7分
,6),E2(6,15)。…7分
27. 解:(1)否。…1分
(2)①解法一:作PD⊥AB于D,则∠PDB=∠PDA=90°,
∵∠ABP=30°,
∴PD=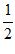 BP。………2分
BP。………2分
∵PB=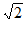 PA,∴PD=
PA,∴PD=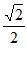 PA。
PA。
∴在Rt△PDA中,由勾股定理可得PD=AD。
∴∠PAB=45°。 …3分
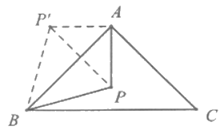
解法二:作点P关于直线AB的对称点P’,连接BP’,P’A,PP’,则∠P’BA=∠PBA,∠P’AB=∠PAB,BP’=BP,AP’=AP。
∵∠ABP=30°,∴∠P’BP=60°。∴△P’BP是等边三角形。∴P’P=BP。
∵PB=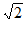 PA,∴P’P=
PA,∴P’P=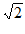 PA。∴P’P2=PA2+P’A2。
PA。∴P’P2=PA2+P’A2。
∴∠PAP’=90°。∴∠PAB=45°。 ……3分
②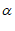 +
+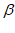 =45°,证明如下: …4分
=45°,证明如下: …4分
作AD⊥AP,并取AD=AP,连接DC,DP。∴∠DAP=90°。
∵∠BAC=90°,∴∠BAC+∠CAP=∠DAP+∠CAP,即∠BAP=∠CAD。
∵AB=AC,AD=AP,∴△BAP≌△CAD。
∴∠1=∠2,PB=CD。
∵∠DAP=90°,AD=AP,∴PD=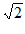 PA,∠ADP=∠APD=45°。
PA,∠ADP=∠APD=45°。
∵PB=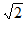 PA,∴PD=PB=CD。∴∠DCP=∠DPC。
PA,∴PD=PB=CD。∴∠DCP=∠DPC。
∵∠APC=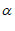 ,∠BPC=
,∠BPC=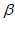 ,
,
∴∠DPC=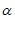 +45°,∠1=∠2=
+45°,∠1=∠2=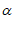 –
–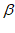 。
。
∴∠3=180°-2∠DPC=90°-2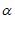 。
。
∴∠ADP=∠1+∠3=90°-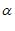 –
–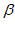 =45°。
=45°。
∴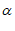 +
+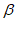 =45°。……7分
=45°。……7分
28. 解:(1)E,G;…………2分
(2)①如图2,
∵M(1,1),P(3,3),N(3,1),
∴MN=2,PN⊥MN,
∵四边形MNPQ是菱形,
∴四边形MNPQ是正方形,
∴S四边称MNPQ=2×2=4;………4分
②b的取值范围是-4≤b≤4。……6分