北京师大附中2020-2021学年下学期高二年级期末考试数学试卷AP
考试时长90分钟,满分100分。
第一部分:学考数学(共70分)
一、选择题:本大题共8题,每小题4分,共32分
1. 已知点M(-1,4)和点N(7,0),x轴上一点P满足|PM|=|PN|,那么点P的坐标为( )
A. (-2,0) B. (1,0) C. (2,0) D. (3,0)
2. 直线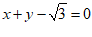 的倾斜角是( )
的倾斜角是( )
A 30° B 45° C 60° D 135°
3. 过点A(1,0)且与直线x-2y-2 =0平行的直线的方程是( )
A x-2y-1=0 B x-2y+1=0
C 2x+y-2=0 D x+2y-1=0
4. 如果直线ax+2y+2=0与直线3x-y-2=0垂直,那么实数a=( )
A -3 B-6 C
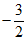 D
D
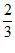
5. 点P(0,2)到直线y=3x的距离是( )
A 1 B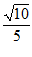 C 2 D
C 2 D
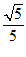
6. 平行线6x+8y+4=0与3x+4y-12=0之间的距离是( )
A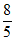 B
B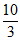 C
C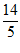 D
D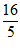
7. 与圆C: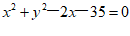 的圆心相同且面积为圆C的一半的圆的方程是( )
的圆心相同且面积为圆C的一半的圆的方程是( )
A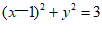 B
B 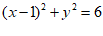
C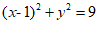 D
D 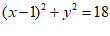
8. 圆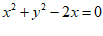 和圆
和圆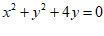 的位置关系是( )
的位置关系是( )
A相离 B外切 C相交 D内切
二、填空题:本大题共5小题,每小题4分,共20分。
9. 以点A(-1,5)和点B(3,-3)为端点的线段的中点坐标是_________。
10. 已知M(-1,-3),N(1,1),P(3,x)三点共线,则实数x=__________。
11. 斜率为-2且在x轴上截距为-1的直线的方程是________。
12. 圆(x-1)2+ (y+2)2= 10在点(2,1)处的切线的方程为_________。
13. 直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长为________。
三、解答题:共2道大题,共18分,请写出解题步骤。
14. (12分)已知直线l:x+2y-2=0,试求:
(1)与直线l的距离为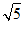 的平行直线的方程;
的平行直线的方程;
(6分)
(2)点P(-2,-1)关于直线l的对称点的坐标. (6分)
15. (6分)已知圆C的圆心在直线x+y-1=0上,且A(-1,4)和B(1,2)是圆C上的两点,求圆C的方程.
第二部分:SAT数学(10道小题,每小题3分,共30分)
1.
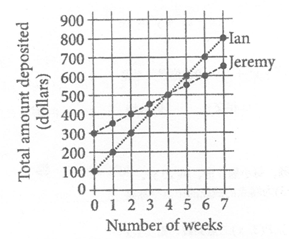
The two graphs above show the total amounts of money that Ian and Jeremy each have deposited into their savings accounts for the first seven weeks after opening their accounts. After they made their initial deposits, how much more did Ian deposit each week than Jeremy?
A)$200
B)$100
C)$50
D)$25
2. A book was on sale for 40% off its original price. If the sale price of the book was $18. 00, what was the original price of the book? (Assume there is no sales tax. )
A)$7.20
B)$10.80
C)$30.00
D)$45.00
3.
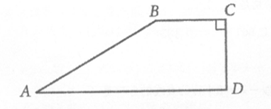
In quadrilateral ABCD above, 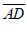 →
→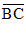 and CD =
and CD =
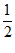 AB. What is the measure of angle B?
AB. What is the measure of angle B?
A)150°
B)135°
C)120°
D)90°
4.
Survey Results
Answer | Percent |
Never | 31.3% |
Rarely | 24.3% |
Often | 13.5% |
Always | 30.9% |
The table above shows the results of a survey in which tablet users were asked how often they would watch video advertisements in order to access streaming content for free. Based on the table, which of the following is closest to the probability that a tablet user answered “Always,” given that the tablet user did not answer “Never”?
A)0.31
B)0.38
C)0.45
D)0.69
5.
Customer Purchases at a Gas Station
Beverage purchased | Beverage not purchased | Total | |
Gasoline purchased | 60 | 25 | 85 |
Gasoline not purchased | 35 | 15 | 50 |
Total | 95 | 40 | 135 |
On Tuesday, a local gas station had 135 customers. The table above summarizes whether or not the customers on Tuesday purchased gasoline, a beverage, both, or neither. Based on the data in the table, what is the probability that a gas station customer selected at random on that day did not purchase gasoline?
A)
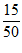
B)
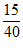
C)
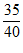
D)
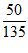
6. Biologists found a new species of pale shrimp at the world’s deepest undersea vent, the Beebe Vent Field. The vent is 3.1 miles below the sea’s surface.
Approximately how many kilometers below the sea’s surface is the vent? (1 kilometer≈0. 6214 miles)
A)2
B)3
C)4
D)5
7. If sin x° =a, which of the following must be true for all values of x?
A)cosx°=a
B)sin (90°- x°)= a
C)cos (90°-x°)= a
D)sin (x2)°=a2
8.
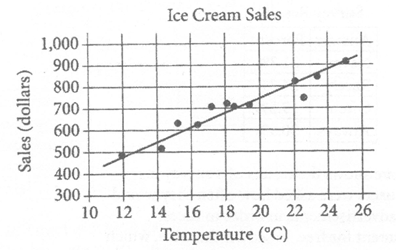
The scatterplot above shows a company’s ice cream sales d, in dollars, and the high temperature t, in degrees Celsius (℃), on 12 different days. A line of best fit for the data is also shown. Which of the following could be an equation of the line of best fit?
A)d=0. 03t+402
B)d=10t+402
C)d=33t+300
D)d=33t+84
9.
h(x)=-16x2+100x+10
The quadratic function above models the height above the ground h,in feet, of a projectile x seconds after it had been launched vertically. If y=h(x)is graphed in the xy-plane, which of the following represents the real-life meaning of the positive x-intercept of the graph?
A)The initial height of the projectile
B)The maximum height of the projectile
C)The time at which the projectile reaches its maximum height
D)The time at which the projectile hits the ground
10. The average annual energy cost for a certain home is $4,334. The homeowner plans to spend $25,000 to install a geothermal heating system. The homeowner estimates that the average annual energy cost will then be $2,712. Which of the following inequalities can be solved to find t, the number of years after installation at which the total amount of energy cost savings will exceed the installation cost?
A)25,000 > (4,334-2,712)t
B)25,000 <(4,334-2,712)t
C)25,000-4,334>2,712t
D)25,000 >
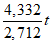
参考答案
第一部分:学考数学(共70分)
一、选择题:本大题共8小题,每小题4分,共32分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | C | D | A | D | B | C | D | C |
二、填空题:本大题共5小题,每小题4分,共20分。
9. (1, 1); 10. 5;
11. 2x+y+2=0; 12. x+3y-5=0
13. 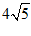
三、解答题:共2道大题,共18分,请写出解题步骤。
14. (1)设所求直线的方程为x+2y+c=0 …………………………2分
则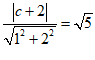 …………………………………………2分
…………………………………………2分
解得c=3或c=-7
所以所求直线的方程为x+2y+3=0或x+2y-7=0 ……………………2分
(2)设P关于l的对称点为Q(x,y),
则PQ⊥l,即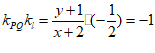 ① ……………………………………2分
① ……………………………………2分
同时线段PQ的中点(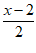 ,
,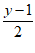 )在直线l上,即
)在直线l上,即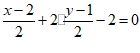 ②——2分
②——2分
联立①②并化简得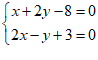
解得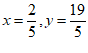 ,即Q(
,即Q(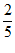 ,
,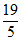 ) …………………………2分
) …………………………2分
15. 线段AB的斜率为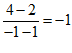 ,中点为(0,3),
,中点为(0,3),
所以圆心C所在的线段AB的中垂线是y-3=1(x-0),即y=x+3 …………………2分
解方程组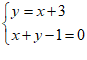
得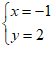 ,即有圆C(-1,2)………………2分
,即有圆C(-1,2)………………2分
半径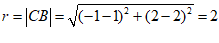
所以圆C的方程是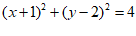 …………………………2分
…………………………2分
第二部分:SAT数学(共30分)
(选择题,共10小题,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | C | A | C | D | D | C | D | D | B |
