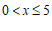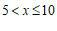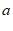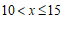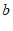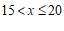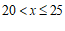北京市顺义区2020-2021学年下学期初中八年级期末教学质量检测数学试卷
一、选择题 (本题共20分,每小题2分)
下列各题均有四个选项,其中只有一个是符合题意的 .
1.在函数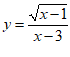 中,自变量
中,自变量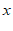 的取值范围是
的取值范围是
A. 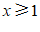 且
且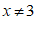 B.
B. 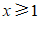 C.
C. 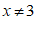 D.
D. 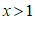 且
且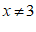
2.把直线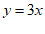 向下平移一个单位长度后,其直线的表达式为
向下平移一个单位长度后,其直线的表达式为
A. 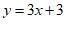 B.
B. 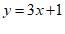 C.
C. 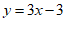 D.
D. 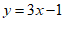
3. 甲、乙两名射击运动员各进行10次射击练习,平均成绩均为8环,这两名运动员成绩的方差分别是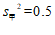 ,
,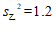 ,则下列说法正确的是
,则下列说法正确的是
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
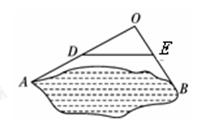
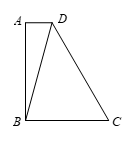
4. 如图,为测量池塘岸边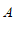 、
、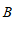 两点的距离,小明在池塘的一侧选取一点
两点的距离,小明在池塘的一侧选取一点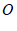 ,测得
,测得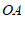 、
、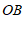 的中点分别是点
的中点分别是点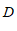 、
、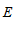 ,且
,且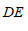
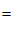
 米,则
米,则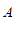 、
、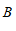 间的距离是
间的距离是
A. 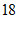 米 B.
米 B. 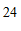 米 C.
米 C. 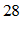 米 D.
米 D. 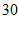 米
米
5.下列各图形中不是中心对称图形的是
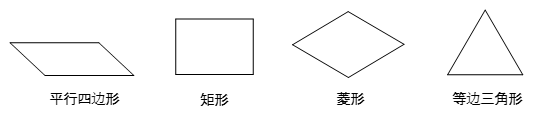
A B C D
6.已知关于x 的一元二次方程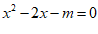 有两个不相等的实数根,则m的取值范围是
有两个不相等的实数根,则m的取值范围是
A. m<-2 B. m>-1 C. m<0 D. m ≥0
7. 用配方法解一元二次方程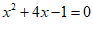 时,此方程可变形为
时,此方程可变形为
A. 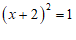 B.
B. 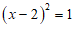 C.
C. 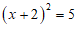 D.
D. 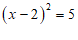
8. 某商场四月份的营业额为36万元,六月份的营业额为48万元,设四月份到六月份的月平均增长率为x,则可列方程为
A. 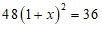 B.
B. 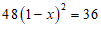
C. 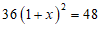 D.
D. 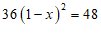
9.若一组数据2,0,1,x,3的平均数是2,则这组数据的方差是
A.1 B.2 C.3 D.4
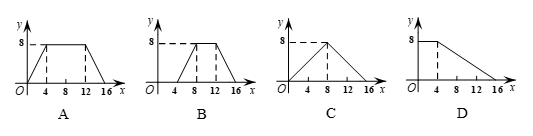
10. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿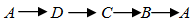 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
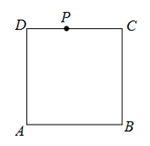
二、填空题 (本题共20分,每小题2分)
11.若点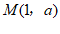 与点
与点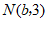 关于y轴对称,则
关于y轴对称,则
,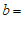
.
12.已知一次函数的图象经过第一、二、四象限,写出一个满足条件的一次函数的表达式
.
13. 已知点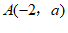 ,
,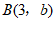 在直线
在直线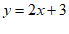 上,则
上,则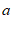
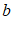 .(填”
.(填”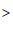 “”
“”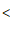 “或”=”号)
“或”=”号)
14. 若一个多边形的内角和是它外角和的2倍, 则这个多边形是
边形.
15. 已知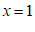 是方程
是方程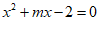 的一个根,则
的一个根,则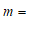
,方程的另一个根是
.
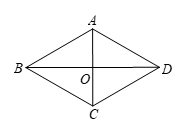
16. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,且AO= CO,BO= DO,要使得四边形ABCD是菱形,应添加的条件是__________(只填写一个条件).
17. 如图,直线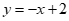 与
与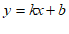 (
(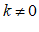 且
且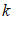 ,
,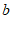 为常数)的交点坐标为(3,-1),则关于x的不等式
为常数)的交点坐标为(3,-1),则关于x的不等式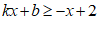 的解集为
的解集为
.
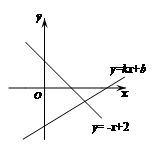
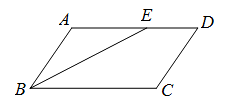
18. 如图,四边形ABCD是平行四边形,BE平分∠ABC,与AD交于点E,BC=5,DE=2,则AB的长为
.
19. 如图,将一张矩形纸片沿对角线BD翻折,点C的对应点为C’,AD与BC’交于点E. 若∠ABE=30°,BC=3,则DE的长为____________.
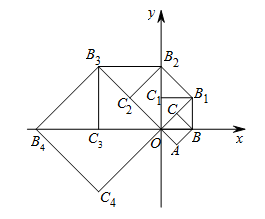
20.如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是
; B2020的坐标是
.
三、解答题 (本题共60分,第21—26小题,每小题5分,第27—31小题,每小题6分)解答应写出文字说明、演算步骤或证明过程.
21.解方程: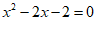 .
.
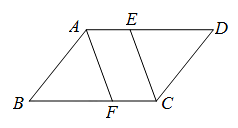
22. 已知:如图,在□ABCD中,E,F分别为边AD,BC上一点,且DE=BF.
求证:四边形AFCE是平行四边形.
23. 某地出租车计费方法如图所示,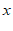 (km)表示行驶里程,
(km)表示行驶里程,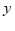 (元)表示车费,请根据图象回答下面的问题:
(元)表示车费,请根据图象回答下面的问题:
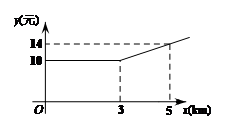
(1)该地出租车的起步价是
元;
(2)当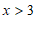 时,求
时,求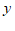 关于
关于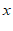 的函数关系式;
的函数关系式;
(3)若某乘客一次乘出租车的车费为40元,求这位乘客乘车的里程.
24. 已知:如图,在□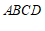 中,
中,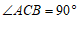 ,过点
,过点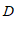 作
作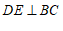 交
交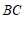 的延长线于点
的延长线于点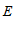 .
.
(1)求证:四边形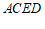 是矩形;
是矩形;
(2)连接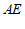 ,若
,若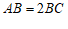 ,求证:
,求证: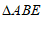 是等边三角形.
是等边三角形.
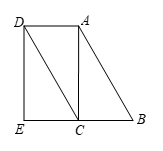
25. 如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.

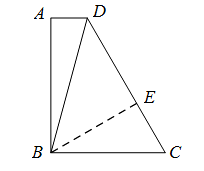
26. 已知:如图,四边形ABCD中,AD∥BC,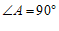 ,BC=2,
,BC=2,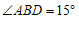 ,
,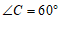 .
.
(1)求∠BDC的度数;
(2)求CD的长.
27. 已知关于x的一元二次方程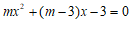 (
(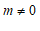 ).
).
(1)求证:方程总有两个实数根;
(2)如果m为正整数,且方程的两个根均为整数,求m的值.
28. 小敏同学为了解2020年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行分组整理,其中月均用水量在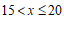 这组的数据是:
这组的数据是:
16,17,17,17,18,18,19,20,20,20 .
随机调查该小区家庭月均用水量频数分布表
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
|
| 0.28 |
| 16 |
|
| 10 | 0.20 |
| 4 | 0.08 |
随机调查该小区家庭月均用水量频数分布直方图
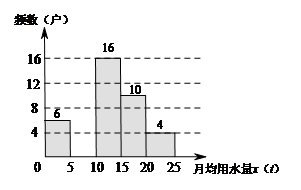
请解答以下问题:
(1)表中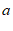 =
=
,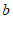 =
=
;
(2)把上面的频数分布直方图补充完整;
(3)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(4)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过18t的家庭大约有多少户?
29. 如图,在平面直角坐标系xOy中,一次函数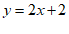 的图象经过点A(-2,m),与y轴交于点B.
的图象经过点A(-2,m),与y轴交于点B.
(1)求点A和点B的坐标;
(2)若点P是直线AB上一点,且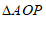 的面积为3, 求点P的坐标.
的面积为3, 求点P的坐标.
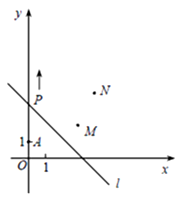
30. 如图,A(0,1),M(3,2),N (4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l: 也随之移动,设移动时间为t秒.
也随之移动,设移动时间为t秒.
(1)当t=3时,求直线l的表达式;
(2)若点M,N位于直线l的两侧,确定t的取值范围.
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
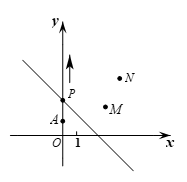
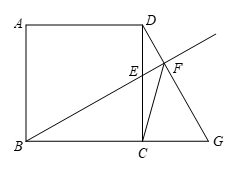
31.已知:如图,在正方形ABCD中,点E是CD上一点,作射线BE,过点D作DF⊥BE于点F,交BC延长线于点G,连接FC.
(1)依据题意补全图形 ;
(2)求证:∠FBC=∠CDG ;
(3)用等式表示线段DF,BF,CF之间的数量关系并加以证明.
【试题答案】
一、选择题
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | D | A | C | D | B | C | C | B | B |
二、填空题
11.3 , -1 ; 12.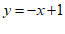 (答案不唯一) ; 13. < ; 14. 六 ;
(答案不唯一) ; 13. < ; 14. 六 ;
15. 1, -2 ; 16.AC⊥BD (或AB=AD); 17. x≥3 ; 18. 3 ; 19. 2 ;
20. (0 , 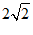 ) ,(
) ,(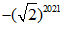 , 0).
, 0).
三、解答题
21.解:解法一: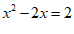 ……………………………………………1分
……………………………………………1分
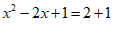
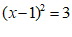 …………………………………………………2分
…………………………………………………2分
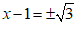 …………………………………………………3分
…………………………………………………3分
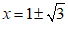 ……………………………………………………4分
……………………………………………………4分
∴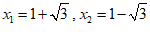 .………………………………… 5分
.………………………………… 5分
解法二: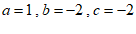 , ………………………………………1分
, ………………………………………1分
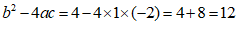 .…………………… 2分
.…………………… 2分
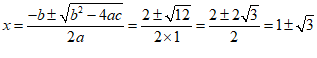 .………4分
.………4分
∴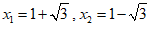 .……………………………………5分
.……………………………………5分
22. 证明: ∵ 四边形ABCD是平行四边形,
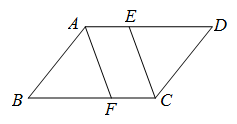
∴ AD∥BC , AD=BC. ………………………………2分
∵ E,F分别为边AD,BC上一点,且DE=BF ,
∴ AE∥FC.
AD-DE=BC-BF 即AE=FC………………………………4分
∴ 四边形AFCE是平行四边形.………………………………5分
23.解:(1)该地出租车的起步价是10元 ………………………………………1分
(2) 当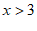 时,设函数表达式为
时,设函数表达式为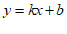
则有 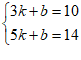 ………………………………………………2分
………………………………………………2分
解得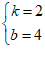 ,
,
所以,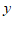 关于
关于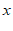 的函数表达式为
的函数表达式为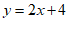 ……………………………4分
……………………………4分
(2)当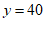 时,即
时,即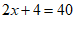 ,
, 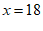
所以,这位乘客乘车的里程是18km ……………………………5分
24. (1)证明:∵□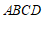 中,
中,
∴ AD∥BC,AD=BC ,AB=DC,…………………1分
∴∠DAC=∠ACB,
∵∠ACB=90º,
∴∠DAC=90º,∠ACE=90º ……………………………2分
∵DE⊥BC
∴ ∠DEC=90º
∴四边形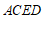 是距形. ………………………3分
是距形. ………………………3分
(2)证明:∵四边形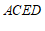 是距形
是距形
∴AD=CE ,AE=DC ………………………4分
∴BC=CE ,AB=AE
∵AB=2BC
∴AB=AE=BE
∴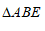 是等边三角形 . ……………………………5分
是等边三角形 . ……………………………5分
25. 解:设小路的宽为xm,依题意有 …………………………1分
(40-x)(32-x)=1140 …………………………3分
整理,得x2-72x+140=0. …………………………4分
解得x1=2,x2=70(不合题意,舍去). ……………5分
答:小路的宽应是2m.
26. 解:(1)∵ AD∥BC,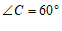 ,
,
∴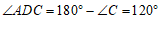 .…………………………1分
.…………………………1分
在Rt△ABD中,
∵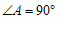 ,
,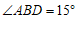 ,
,
∴ 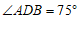 . …………………………………………2分
. …………………………………………2分
∴ 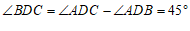 . ……………3分
. ……………3分
(2)作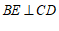 于点E.
于点E.
在Rt△BCE中,
∵ BC=2, ,
,
∴
∴ .
.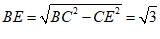 ………4分
………4分
∵ 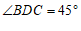 ,
,
∴ 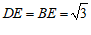 .
.
∴ 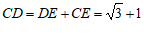 . ……………………5分
. ……………………5分
27. (1)证明: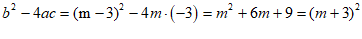 ,…1分
,…1分
∵ 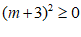 ,
,
∴ 方程总有两个实数根. ……………………………………………3分
(2)解:∵ 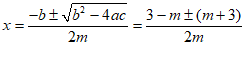 ,
,
∴ 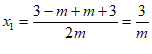 ,
,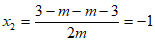 . ………5分
. ………5分
∵方程的两个根均为整数,且m为正整数,
∴m为1或3. ……………………………………………………6分
28. 解:(1)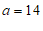 ,
, 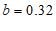 …………………………………………………2分
…………………………………………………2分
(2) 补全的图形如图.
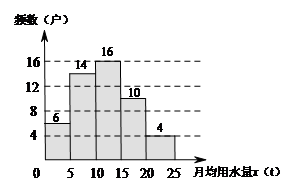
………………………………………………4分
(3)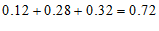 .
.
即月均用水量不超过15t的家庭占被调查的家庭总数的72%. ………………5分
(4)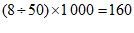 .
.
所以根据调查数据估计,该小区月均用水量超过18t的家庭大约有160户……6分
29. 解:(1)∵一次函数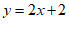 的图象经过点A(-2,m),与y轴交于点B.
的图象经过点A(-2,m),与y轴交于点B.
∴ 令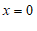 ,则
,则 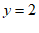 …………………………………………………………1分
…………………………………………………………1分
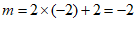
∴ A(-2,-2),B(0 , 2) …………………………………………2分
(2) 连结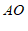 , 则
, 则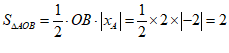
∵点P是直线AB上一点,且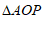 的面积为3
的面积为3
∴点P不可能在线段AB上.
当点P在第一象限时,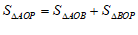 ,
,
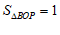 ………………………………………………………………3分
………………………………………………………………3分
∴ 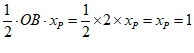
∴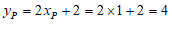
∴点P的坐标为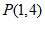 …………………………………………………4分
…………………………………………………4分
当点P在第三象限时,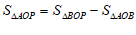 ,
,
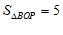 ………………………………………………………………5分
………………………………………………………………5分
∴ 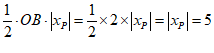
∴ 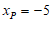
∴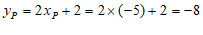
∴点P的坐标为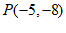 … …………………………………………6分
… …………………………………………6分
综上,点P的坐标为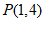 和
和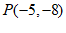
30. 解:(1)直线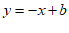 交
交 轴于点
轴于点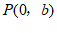 ,
,
由题意,得 ,
, ,
,
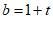 .
.
当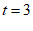 时,
时,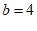 .
.
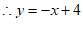 . ……………………………………2分
. ……………………………………2分
(2)当直线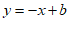 过
过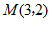 时,
时,
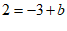 .
.
解得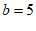 .
.
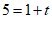 .
.
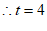 . ……………………………………3分
. ……………………………………3分
当直线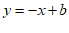 过
过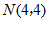 时,
时,
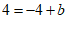 .
.
解得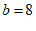 .
.
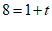 .
.
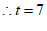 .
.
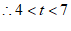 .……………………………………4分
.……………………………………4分
(3)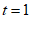 时,落在
时,落在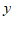 轴上; ……………………5分
轴上; ……………………5分
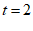 时,落在
时,落在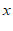 轴上. ……………………6分
轴上. ……………………6分
31. (1)依据题意补全图形,如图
 ……………………………………1分
……………………………………1分
(2)证明: ∵ 四边形ABCD是正方形
∴ ∠BCD=90º
∴ ∠FBC=90º-∠BEC …………………………………2分
∵ DF⊥BE
∴ ∠DFE=90º
∴ ∠CDG=90º-∠DEF
∵ ∠BEC=∠DEF
∴ ∠FBC=∠CDG ……………………………………3分
(3) 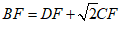 ……………………………………4分
……………………………………4分
证明:
过点C作HC⊥CF ,HC交BF于点H,…………5分
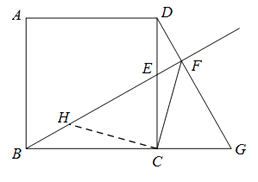
∴ ∠BCH+∠HCD=90º,∠DCF+∠HCD=90º
∴ ∠BCH=∠DCF
又∵ ∠FBC=∠CDG ,BC=DC
∴ △BCH≌△DCF
∴ BH=DF ,CH=CF
∴ △HCF是等腰直角三角形
∴ 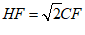 ………………… 6分
………………… 6分
∴ 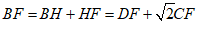

 (t)
(t)