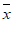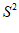北京市通州区2020-2021学年下学期初中八年级期末调研数学试卷
本试卷共三道大题,28个小题,满分为100 分,考试时间为120 分钟.
一、选择题(本题共8个小题,每小题2分,共16分)每题均有四个选项,符合题意的选项只有一个.
1.方程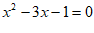 的二次项系数和一次项系数分别为
的二次项系数和一次项系数分别为
A. 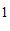 和
和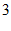 B.
B. 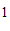 和
和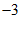 C.
C. 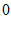 和
和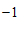 D.
D. 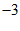 和
和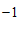
2.下列图形中,既是轴对称图形,又是中心对称图形的是



A. B. C. D.
3.在平面直角坐标系xOy中,过点P(-2,3)作PA⊥y轴,垂足为点A,那么PA的长为
A. 2 B. 3 C. 5 D. 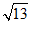
4.方程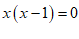 的解是
的解是
A. 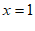 B.
B. 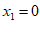 ,
,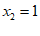
C. 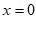
D. 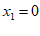 ,
,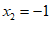
5.甲、乙、丙、丁四名学生参加区中小学生运动会跳高项目预选赛,他们8次跳高的平均成绩及方差如下表所示,要选一位成绩较好且稳定的运动员去参赛,应选运动员是
甲 | 乙 | 丙 | 丁 | |
| 1.72 | 1.75 | 1.75 | 1.72 |
| 1 | 1.3 | 1 | 1.3 |
A. 甲 B. 乙 ( C)丙 D. 丁
6.用配方法解一元二次方程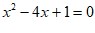 ,配方变形过程正确的是
,配方变形过程正确的是
A. 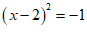 B.
B. 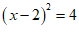 C.
C. 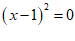 D.
D. 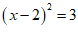
7.如图,E是平行四边形ABCD边BC上一点,且AB=BE,连接AE,并延长AE与DC的延长线交于点F,如果∠F=70°,那么∠B的度数是
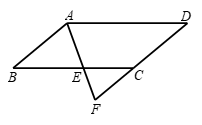
A. 30° B. 40° C. 50° D. 70°
8.小明步行从家出发去学校,步行了5分钟时,发现作业忘在家,马上以同样的速度回家取作业,然后骑共享单车赶往学校,小明离家距离S(米)与时间t(分钟)之间的函数图象如图,那么小明骑车比步行的速度每分钟快
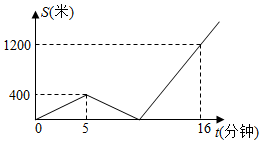
A. 200米 B. 80米 C. 140米 D. 120米
二、填空题(本题共8个小题,每小题2分,共16分)
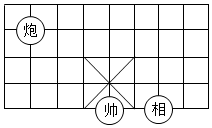
9.如图,在象棋棋盘上建立平面直角坐标系,如果使”帅”的位置为点( ,
,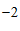 ),”相”的位置为点(
),”相”的位置为点(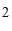 ,
,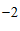 ),那么”炮”的位置为点 .
),那么”炮”的位置为点 .
10.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从一个n边形的一个顶点出发最多引出3条对角线,那么这个n边形的内角和是 .
11.
如果一元二次方程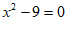 的两根分别是a,b,且a>b,那么a的值是_____________.
的两根分别是a,b,且a>b,那么a的值是_____________.
12.已知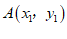 ,
,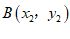 是一次函数y=kx+3的图象上两点,当x1<x2时,则y1>y2,那么k的值可以是 (写出一个满足题意k的值即可).
是一次函数y=kx+3的图象上两点,当x1<x2时,则y1>y2,那么k的值可以是 (写出一个满足题意k的值即可).
13 . 如果关于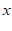 的一元二次方程
的一元二次方程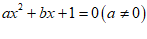 的一个解是
的一个解是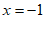 ,那么代数式
,那么代数式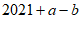 的值是 .
的值是 .
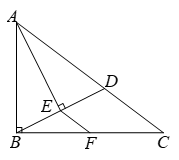
14.如图,在△ABC中,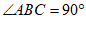 ,在边AC上截取AD=AB,连接BD,过点A作AE⊥BD于点E. 已知AB=6,BC=8,如果 F是边BC的中点,连接EF,那么EF的长是_________________.
,在边AC上截取AD=AB,连接BD,过点A作AE⊥BD于点E. 已知AB=6,BC=8,如果 F是边BC的中点,连接EF,那么EF的长是_________________.
15. 在对一组样本数据进行分析时,某同学列出了方差的计算公式: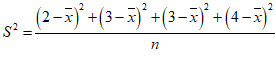 ,
,
并由公式得出以下信息:①样本的容量是4,②样本的中位数是3,③样本的众数是3,④样本的平均数是3.5,⑤样本的方差是0.5,那么上述信息中正确的是______________________(只填序号).
16.《九章算术》是我国古代的数学名著,其中”勾股”章有一题,大意是说:已知矩形门的高比宽多6尺,门的对角线长10尺,那么门的高和宽各是多少?如果设门的宽为x尺,根据题意,那么可列方程_________________.
三、解答题(本题共68分,第17~22题,每小题5分,第23~26题,每小题6分,第27~28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17. 解方程: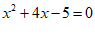 .
.
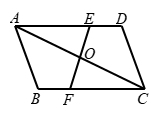
18.如图,在
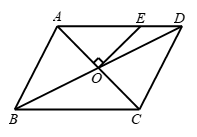
▱ABCD中,点E,F分别在AD、BC上,且AE=CF,连接EF,AC交于点O.求证:OE=OF.
19.已知关于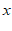 的一元二次方程
的一元二次方程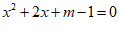 有两个实数根.
有两个实数根.
(1)求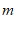 的取值范围;
的取值范围;
(2)当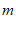 取最大整数时,求此时方程的根..
取最大整数时,求此时方程的根..
20 . 已知一次函数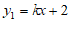 的图象与
的图象与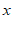 轴交于点
轴交于点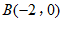 ,与正比例函数
,与正比例函数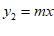 的图象交于点
的图象交于点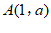 .
.
(1)分别求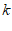 ,
,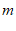 的值;
的值;
(2)点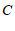 为
为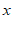 轴上一动点.如果△
轴上一动点.如果△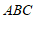 的面积是
的面积是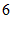 ,请求出点
,请求出点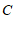 的坐标.
的坐标.
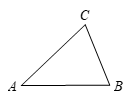
21. 已知:在△ 中,
中,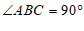 .
. 
求作:矩形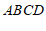 .
.
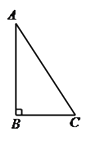
作法:如下,
①分别以点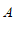 ,
,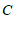 为圆心,大于
为圆心,大于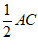 的同样长为半径作弧,两弧分别交于点
的同样长为半径作弧,两弧分别交于点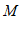 ,
,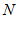 ;
;
②作直线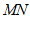 ,交边
,交边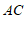 于点
于点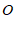 ;
;
③作射线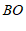 ,以点
,以点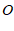 为圆心,以
为圆心,以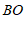 长为半径作弧,与射线
长为半径作弧,与射线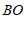 的另一个交点为
的另一个交点为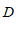 ,连接
,连接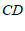 ,
,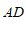 ;
;
所以四边形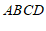 就是所求作的矩形.
就是所求作的矩形.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: ∵直线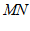 是
是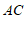 的垂直平分线,
的垂直平分线,
∴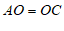 .
.
∵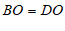 ,
,
∴四边形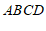 是平行四边形(____________________________________)(填推理的依据).
是平行四边形(____________________________________)(填推理的依据).
∵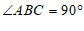 ,
,
∴四边形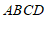 是矩形(____________________________________)(填推理的依据).
是矩形(____________________________________)(填推理的依据).
22. 已知关于x的方程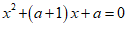 .
.
(1)不解方程,判断方程根的情况,并说明理由;
(2)如果该方程有一个根大于0,求a的取值范围.
23.如图,在▱ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,如果AE=4,DE=2,DC=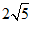 ,
,
求AC的长.
24. 在平面直角坐标系xOy中,将点A(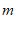 ,2)向右平移3个单位长度,得到点B,点B在直线
,2)向右平移3个单位长度,得到点B,点B在直线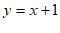 上.
上.
(1)求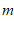 的值和点B的坐标;
的值和点B的坐标;
(2)如果一次函数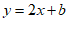 的图象与线段AB有公共点,求
的图象与线段AB有公共点,求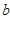 的取值范围.
的取值范围.
25.今年7月1日是中国共产党建党100周年纪念日,为了让学生进一步了解中国共产党的历史,某学校组织了一系列”党史知识”专题学习活动,对八年级甲,乙两班各40名学生进行了”党史”相关知识的测试,并分别抽取了15份成绩,并对成绩(百分制并取整数)进行整理、描述和分析,部分信息如下:
a. 甲班、乙班15名学生测试成绩统计如下:(满分100分)
甲班:68,72,89,85,82,85,74,92,80,85,78,85,69,76,80.
乙班:86,89,83,76,73,78,67,80,80,79,80,84,82,80,83.
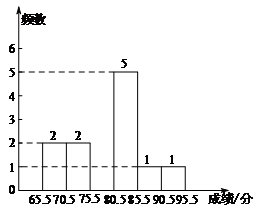
b. 甲班15名学生测试成绩的频数分布直方图(不完整):
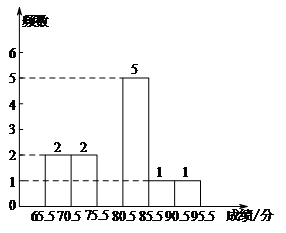
c. 乙班15名学生测试成绩的频数分布表:
组别 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
乙 | 1 | 1 | a | b | 2 | 0 |
d. 甲班、乙班15名学生测试成绩的平均数、众数、中位数和方差如下:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 80 | x | 80 | 47.6 |
乙 | 80 | 80 | y | 26.2 |
根据以上信息,回答下列问题.
(1)补全甲班测试成绩的频数分布直方图;
(2)在乙班15名学生测试成绩的频数分布表中,a= ,b= .
(3)在甲班、乙班15名学生测试成绩的平均数、众数、中位数、方差表中,x= ,y= .
(4)你认为哪个班的学生掌握”党史”相关知识的整体水平较好,说明理由.
26. 如图,在平面直角坐标系xOy中,一次函数y=kx+4(k≠0)的图象与y轴交于点C,已知点A(2,0),B(4,2).
(1)求点C的坐标;
(2)直接判断线段CA、CB的大小关系: CA______CB(填”>”,”=”或”<“)
(3)如果点A(2,0),B(4,2)到一次函数y=kx+4(k≠0)图象的距离相等,求k的值.
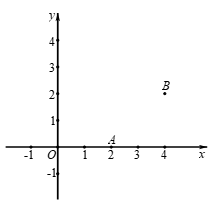
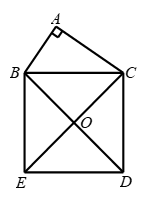
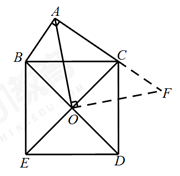
27.如图, 在△ABC中,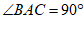 ,以BC为边,向外作正方形BCDE,对角线BD,CE交于点O.
,以BC为边,向外作正方形BCDE,对角线BD,CE交于点O.
(1)求证: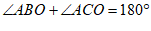 ;
;
(2)连接AO, 用等式表示线段AB,AC,AO之间的数量关系,并证明你的结论.
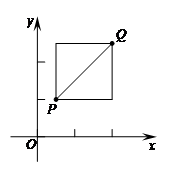
28. 在平面直角坐标系xOy中,对于点P,如果点Q满足条件:以线段PQ为对角线的正方形,且正方形的边分别与x轴,y轴平行,那么称点Q为点P的”和谐点”,如下图所示.
已知点D(-1,2),E(1,2),F(-1,-2).
(1)已知点A的坐标是(2,1).
①在D,E,F中,是点A的”和谐点”的是
.
②已知点B的坐标为(0,b),如果点B为点A的”和谐点”,求b的值;
(2)已知点C(m,0),如果线段DE上存在一个点M,使得点M是点C的”和谐点”,直接写出m的取值范围.
【试题答案】
一、选择题(本题共8个小题,每小题2分,共16分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | A | B | C | D | B | D |
二、填空题(本题共8个小题,每小题2分,共16分)
9. 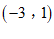
10.
 11.
11. 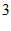 12.
12. 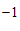 (答案不唯一) 13.
(答案不唯一) 13. 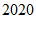 14.
14. 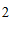 15. ① ②③⑤
15. ① ②③⑤
16. 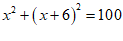 或
或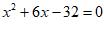
三、解答题(本题共68分,第17~22题,每小题5分,第23~26题,每小题6分,第27~28题,每小题7分)
17. 解: 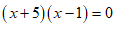 , ………………… 2分
, ………………… 2分
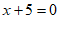 或
或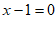 ………………… 4分
………………… 4分
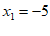 ,
,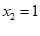 ; ………………… 5分
; ………………… 5分
18.证明: ∵四边形ABCD是平行四边形,
∴ 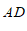 ∥
∥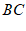 , ………………… 1分
, ………………… 1分
∴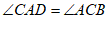 . ………………… 2分
. ………………… 2分
在△AOE和△COF 中
∵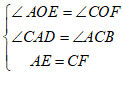
∴ △AOE △COF ………………… 4分
∴ OE = OF. ………………… 5分
19. 解:(1)∵关于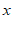 的一元二次方程
的一元二次方程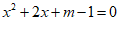 有两个实数根,
有两个实数根,
∴△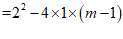 ………………… 1分
………………… 1分
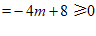
∴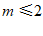 ………………… 2分
………………… 2分
(2)∵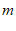 取最大整数,
取最大整数,
∴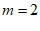 ………………… 3分
………………… 3分
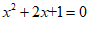 ,
,
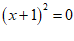 , ………………… 4分
, ………………… 4分
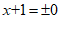
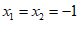 ………………… 5分
………………… 5分
20. 解:(1)∵一次函数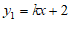 的图象与
的图象与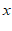 轴交于点
轴交于点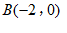 ,
,
∴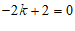
∴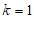 ………………… 1分
………………… 1分
∴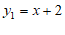
∵一次函数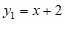 的图象与正比例函数
的图象与正比例函数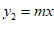 的图象交于点
的图象交于点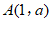 ,
,
∴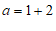 ,
,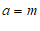 , ………………… 2分
, ………………… 2分
∴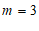 . ………………… 3分
. ………………… 3分
(2)设点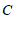 的坐标为
的坐标为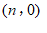 ,过点
,过点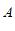 作AD⊥x轴,垂足为点D.
作AD⊥x轴,垂足为点D.
∵△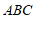 的面积是
的面积是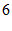 ,
,
∴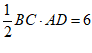
∴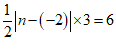
∴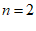 或
或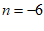
∴点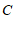 的坐标为
的坐标为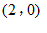 或
或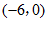 ………………… 5分
………………… 5分
或过点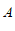 作AD⊥x轴,垂足为点D.
作AD⊥x轴,垂足为点D.
∵△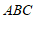 的面积是
的面积是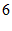 ,
,
∴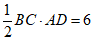
∴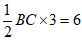
∴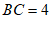 ,
,
∵点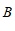 的坐标为
的坐标为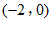 ,
,
∴点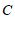 的坐标为
的坐标为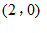 或
或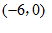
21. (1)画图正确 ………………… 3分
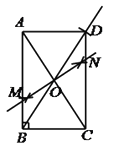
(2)完成下面的证明.
证明: ∵直线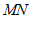 是
是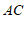 的垂直平分线,
的垂直平分线,
∴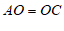 .
.
∵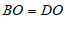 ,
,
∴四边形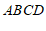 是平行四边形(对角线互相平分的四边形是平行四边形)(填推理的依据). ………………… 4分
是平行四边形(对角线互相平分的四边形是平行四边形)(填推理的依据). ………………… 4分
∵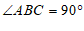 ,
,
∴四边形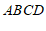 是矩形(有一个角是直角的平行四边形是矩形)(填推理的依据).
是矩形(有一个角是直角的平行四边形是矩形)(填推理的依据).
………………… 5分
22. 解:(1)△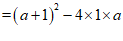 ………………… 1分
………………… 1分
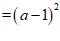
无论a取何值,都有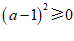 , ………………… 2分
, ………………… 2分
即△≥0
∴方程总有两个实数根. ………………… 3分
(2)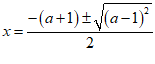 或
或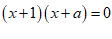
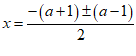
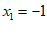 ,
,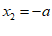 ………………… 4分
………………… 4分
∵方程有一个根大于0,
∴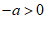
∴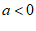 . ………………… 5分
. ………………… 5分
23.解:连接EC. ………………… 1分
∵四边形ABCD是平行四边形,
∴AO=OC, ………………… 2分
∵OE⊥AC,
∴OE是线段AC的垂直平分线,
∴EC=AE= 4, ………………… 3分
在△DEC中,
∵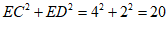 ,
,
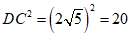
∴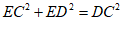 , ………………… 4分
, ………………… 4分
∴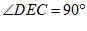 ,
,
∴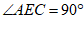 ………………… 5分
………………… 5分
∴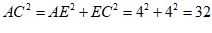 ,
,
∴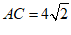 (舍负). ………………… 6分
(舍负). ………………… 6分
24. 解:(1)∵将点A(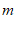 ,2)向右平移3个单位长度,得到点B,
,2)向右平移3个单位长度,得到点B,
∴B(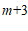 ,2) ………………… 1分
,2) ………………… 1分
∵点B在直线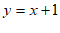 上
上
∴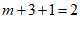
∴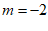 ………………… 2分
………………… 2分
∴点B的坐标为(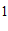 ,2) ………………… 3分
,2) ………………… 3分
或把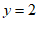 代入
代入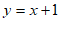 中,
中,
∴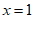
∴点B的坐标为(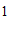 ,2),
,2),
∵点B是由点A(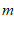 ,2)向右平移3个单位长度得到的,
,2)向右平移3个单位长度得到的,
∴点A的坐标为(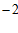 ,2),
,2),
∴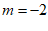
(2) 把点A(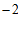 ,2)代入
,2)代入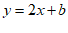 中,
中,
∴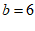 , ………………… 4分
, ………………… 4分
把点B(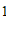 ,2)代入
,2)代入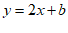 中,
中,
∴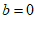 , ………………… 5分
, ………………… 5分
∴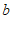 的取值范围是
的取值范围是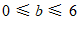 . ………………… 6分
. ………………… 6分
25. 解:(1)补全甲班测试成绩的频数分布直方图置正确;……………… 1分
(2)在乙班15名学生测试成绩的频数分布表中,a=7,b=4. ……………… 3分
(3)在甲班、乙班15名学生测试成绩的平均数、众数、中位数、方差表中x=85,y=80 ………… 5分
(4)你认为哪个班的学生掌握”党史”相关知识的整体水平较好,说明理由.
乙班,因为甲班、乙班15名学生测试成绩的平均数一样,而乙班15名学生测试成绩的方差比甲班小.………………… 1分
26. 解:(1)∵令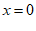 ,
,
∴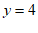
∴点C的坐标为(0,4) ………………… 1分
(2)”=” ………………… 2分
(3)当直线AB与一次函数y=kx+4(k≠0)图象平行时,………………… 3分
设直线AB的表达式为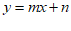
∴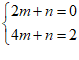
解得: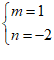
∴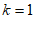 ………………… 4分
………………… 4分
当一次函数y=kx+4(k≠0)图象过线段AB的中点时,
设线段AB的中点为D,
∴点D的坐标为(3,1)
∵CA=CB
∴CD⊥AB,
∴点A(2,0),B(4,2)到一次函数y=kx+4(k≠0)图象的距离相等…………5分
∴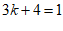
∴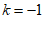 . ………………… 6分
. ………………… 6分
∴k的值为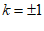
27.证明:(1)
∵四边形BEDC是正方形,
∴BD⊥EC, ………………… 1分
∴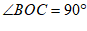
在四边形ABOC中,
∴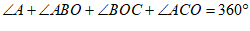 , ………………… 2分
, ………………… 2分
∵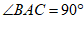 ,
,
∴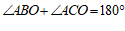 ………………… 3分
………………… 3分
(2)线段AB,AC,AO之间的数量关系是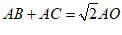
过点O作OF⊥AO,交AC的延长线于点F. …………………4分
∴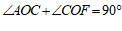 ,
,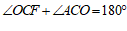 ,
,
∵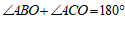
∴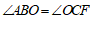 .
.
∵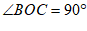
∴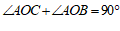
∴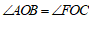
∵四边形BEDC是正方形,
∴OB=OC,
在△ABO和△FCO中,
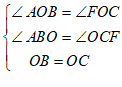 ,
,
∴△ABO ≌△FCO,
∴AB=FC, AO=FO, ………………… 5分
∴ △AOF是等腰直角三角形,
∴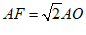 ………………… 6分
………………… 6分
∴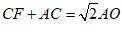
∴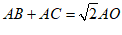 . ………………… 7分
. ………………… 7分
28. 解:(1)①E,F ………………… 2分
②过点A作AM⊥y轴于点M,
∴点M的坐标为(0,1)且AM=2,
∵点B为点A的”和谐点”,
∴BM=2, ………………… 3分
∴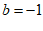 或
或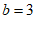 ………………… 5分
………………… 5分
(2)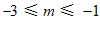 或
或 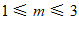 ………………… 7分
………………… 7分