北京101中学2023届上学期高三年级9月月考数学试卷
一、选择题共10小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合M={x∈Z|1g(x-1)≤0},N={x∈Z|x|<2},则M N=(
N=(
)
A. 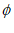 B. (1,2) C. (-2,2] D. {-1,0,1,2}
B. (1,2) C. (-2,2] D. {-1,0,1,2}
2. 如果-1,a,b,c,-9成等比数列,那么(
)
A. b=3,ac=9 B. b=-3,ac=9 C. b=3,ac=-9 D. b=-3,ac=-9
3. 设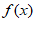 ,
,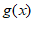 都是单调函数,有如下四个命题:
都是单调函数,有如下四个命题:
①若 单调递增,
单调递增,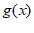 单调递增,则
单调递增,则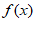 –
–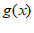 单调递增;
单调递增;
②若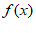 单调递增,
单调递增,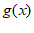 单调递减,则
单调递减,则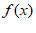 –
–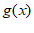 单调递增;
单调递增;
③若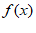 单调递减,
单调递减,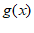 单调递增,则
单调递增,则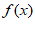 –
–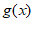 单调递减;
单调递减;
④若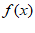 单调递减,
单调递减,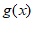 单调递减,则
单调递减,则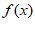 –
–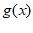 单调递减。
单调递减。
其中,正确的命题是(
)
A. ①③ B. ①④ C. ②③ D. ②④
4. 若ab>0,且a<b,则下列不等式一定成立的是(
)
A. 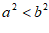 B.
B. 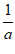 <
<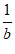 C.
C. 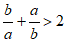 D.
D. 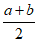 >
>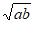
5. 已知△ABC中,角A,B,C所对的边分别为a,b,c,若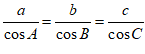 ,则△ABC是(
,则△ABC是(
)
A. 钝角三角形 B. 等边三角形
C. 等腰直角三角形 D. 直角三角形,但不是等腰三角形
6. 已知函数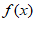 =cos2
=cos2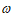 x-sin2
x-sin2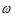 x(
x(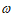 >0)的最小正周期为
>0)的最小正周期为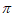 ,则(
,则(
)
A. 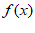 在(0,
在(0,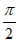 )内单调递增
)内单调递增
B. 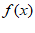 在(0,
在(0,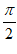 )内单调递减
)内单调递减
C. 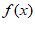 在(
在(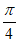 ,
,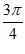 )内单调递增
)内单调递增
D. 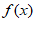 在(
在(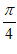 ,
,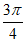 )内单调递减
)内单调递减
7. 若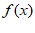 是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)–f(4)=(
是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)–f(4)=(
)
A. -1 B. 1 C. -2 D. 2
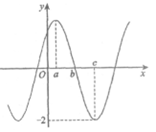
8. 下图是下列四个函数中的某个函数在区间[-3,3]的大致图像,则该函数是(
)
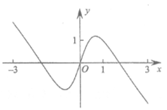
A. 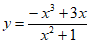 B.
B. 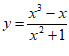 C.
C. 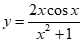 D.
D. 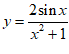
9. 已知函数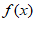 =x3+x2-2|x|-k。若存在实数x0,使得f(–x0)=–f(x0)成立,则实数k的取值范围是(
=x3+x2-2|x|-k。若存在实数x0,使得f(–x0)=–f(x0)成立,则实数k的取值范围是(
)
A. [-1,+∞) B. (-∞,-1] C. [0,+∞) D. (-∞,0]
10. 信息熵是信息论中的一个重要概念。设随机变量X所有可能的取值为1,2,…,n,且P(X=i)=pi>0(i=1,2,…,n),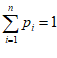 ,定义X的信息熵H(X)=
,定义X的信息熵H(X)=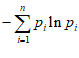 。给出下面四个结论:
。给出下面四个结论:
①若n=1,则H(x)=0;
②若n=2,则当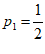 时,H(x)取得最小值;
时,H(x)取得最小值;
③若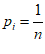 ,则H(x)随着n的增大而增大;
,则H(x)随着n的增大而增大;
④若n=10,随机变量Y所有可能的取值为1,2,…,5,且P(Y=j)=pj+p11-j(j=1,2,…,5),则H(X)>H(Y)。
其中,正确结论的个数是(
)
A. 1 B. 2 C. 3 D. 4
二、填空题共5小题。
11. 在△ABC中,a=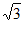 ,b=2
,b=2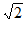 ,B=2A,则cosA=___________。
,B=2A,则cosA=___________。
12. 若函数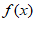 =
=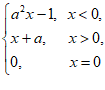 为奇函数,则参数a的值为___________。
为奇函数,则参数a的值为___________。
13. 已知数列{an}满足an+1=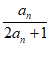 ,n∈N*,若a3=
,n∈N*,若a3=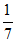 ,则a1=____________。
,则a1=____________。
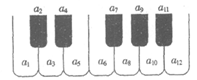
14. 如图,将钢琴上的12个键依次记为a1,a2,…,a12,设1≤i<j<k≤12。若k–j=3且j–i=4,则称ai,aj,ak为原位大三和弦;若k–j=4且j–i=3,则称ai,aj,ak为原位小三和弦。用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为__________。
15. 已知函数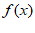 =sin2x–x3,若函数
=sin2x–x3,若函数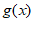 =f(x-4)+
=f(x-4)+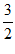 x,则函数
x,则函数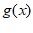 的图像的对称中心为__________;若数列{an}为等差数列,a1+a2+a3+…+a11=44,则g(a1)+g(a2)+…+g(a11)=__________。
的图像的对称中心为__________;若数列{an}为等差数列,a1+a2+a3+…+a11=44,则g(a1)+g(a2)+…+g(a11)=__________。
三、解答题共6小题。解答应写出文字说明、演算步骤或证明过程。
16. 已知函数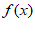 =A sin(
=A sin(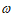 x+
x+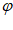 )(A>0,
)(A>0,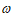 >0,0<
>0,0<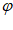 <
<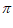 )的部分图像如图所示,在条件①、条件②、条件③这三个条件中选择两个作为已知。
)的部分图像如图所示,在条件①、条件②、条件③这三个条件中选择两个作为已知。
(1)求函数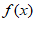 的解析式;
的解析式;
(2)设函数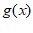 =
=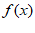 ·cos(2x+
·cos(2x+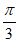 ),若
),若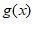 在区间[0,m]上单调递减,求m的最大值。
在区间[0,m]上单调递减,求m的最大值。
条件①:c-a=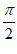 ;
;
条件②:b=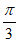 ;
;
条件③:c=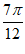 。
。
17. 记Sn为等差数列{an}的前n项和,已知S9=–a5。
(1)若a3=4,求{an}的通项公式;
(2)若a1>0,求使得Sn≥an的n的取值范围。
18. 记△ABC的内角A,B,C的对边分别为a,b,c,以a,b,c为边长的三个正三角形的面积分别为S1,S2,S3,且S1-S2+S3=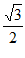 ,sin B=
,sin B=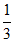 。
。
(1)求△ABC的面积;
(2)若sinA sinC=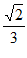 ,求b。
,求b。
19. 已知函数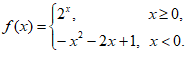
(1)求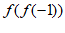 的值;
的值;
(2)求不等式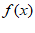 >1的解集;
>1的解集;
(3)当x0<0时,是否存在使得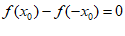 成立的x0值?若存在,直接写出x0的值;若不存在,说明理由。
成立的x0值?若存在,直接写出x0的值;若不存在,说明理由。
20. 已知函数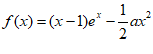 (a
(a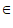 R)。
R)。
(1)当a=0时,求曲线y=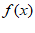 在x=0处的切线方程;
在x=0处的切线方程;
(2)求函数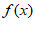 在[1,2]上的最小值。
在[1,2]上的最小值。
21. 已知数列A:a1,a2,…,aN(N≥4),其中a1,a2,…,aN∈Z,且a1<a2<…<aN。
若数列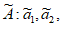 …,
…,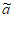 N满足
N满足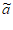 1=a1,
1=a1,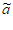 N=aN,当i=2,3,…,N-1时,
N=aN,当i=2,3,…,N-1时,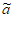 i=ai-1+1或ai+1-1,则称
i=ai-1+1或ai+1-1,则称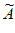 :
: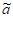 1,
1,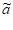 2,…,
2,…,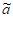 N为数列A的“紧数列“。
N为数列A的“紧数列“。
例如,数列A:2,4,6,8的所有“紧数列“为2,3,5,8;2,3,7,8;2,5,5,8;2,5,7,8。
(1)直接写出数列A:1,3,6,7,8的所有“紧数列“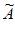 ;
;
(2)已知数列A满足:a1=1,aN=2N,若数列A的所有“紧数列“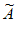 均为递增数列,求证:所有符合条件的数列A的个数为N+1;
均为递增数列,求证:所有符合条件的数列A的个数为N+1;
(3)已知数列A满足:a1=0,a2=2,对于数列A的一个“紧数列“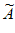 ,定义集合S(
,定义集合S(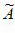 )={ai–
)={ai–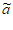 i|i=2,3,…,N-1},如果对任意x∈S(
i|i=2,3,…,N-1},如果对任意x∈S(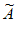 ),都有–x
),都有–x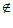 S(
S(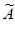 ),那么称
),那么称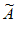 为数列A的“强紧数列“。若数列A存在“强紧数列“,求aN的最小值。(用关于N的代数式表示)
为数列A的“强紧数列“。若数列A存在“强紧数列“,求aN的最小值。(用关于N的代数式表示)
参考答案
1. D
2. (2006高考北京文6)B
3. (2001高考全国理10)C
4. (2022房山一模3)C
5. (2022朝阳高一下期末4)B
6. (2022昌平高三上期末7)B
7. (2010高考安徽理4)A
8. (2022高考全国乙文8)A
设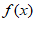 =
=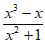 ,则f(1)=0,故排除B;设h(x)=
,则f(1)=0,故排除B;设h(x)=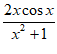 ,当x∈(0,
,当x∈(0, )时,0<cosx<1,所以h(x)=
)时,0<cosx<1,所以h(x)=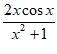 <
<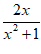 ≤1,故排除C;设
≤1,故排除C;设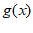 =
=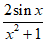 ,则g(3)=
,则g(3)=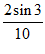 >0,故排除D。
>0,故排除D。
9. (2019海淀高三上期中7)A
由f(–x0)=–f(x0)得–x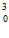 +x
+x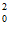 -2|x0|-k=–(x
-2|x0|-k=–(x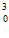 +x
+x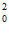 -2|x0|-k),整理得k=x
-2|x0|-k),整理得k=x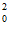 -2|x0|,所以k∈[-1,+∞)。
-2|x0|,所以k∈[-1,+∞)。
10. (2020高考山东(改编)12)C
11. (2021丰台一模13)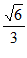 。
。
12. (2022高考上海8)1。
13. (2022东城高二上期末13)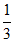 。
。
14. (2020高考全国II文(改编)3)10。
15. (原创)(4,6),66。
16. (2022西城高三上期末17)
(1)选条件①②;
因为c-a=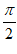 ,所以
,所以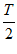 =
=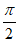 ,即T=
,即T=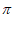 ,则
,则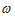 =
=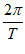 =2。
=2。
由题意可知A=2,则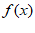 =2sin(2x+
=2sin(2x+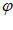 )。
)。
因为b=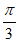 ,f(b)=2sim(
,f(b)=2sim(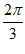 +
+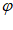 )=0,
)=0,
所以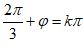 ,k
,k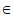 Z,即
Z,即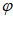 =
=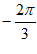 +k
+k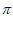 。
。
因为0<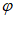 <
<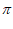 ,所以
,所以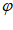 =
=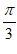 ,k=1。
,k=1。
所以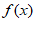 =2sin(2x+
=2sin(2x+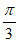 )。
)。
选条件①③:
因为c-a=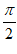 ,所以
,所以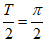 ,即T=
,即T=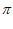 ,则
,则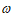 =
=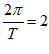 。
。
由题意可知A=2,则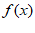 =2sin(2x+
=2sin(2x+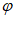 )。
)。
因为c=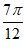 ,f(c)=2sin(
,f(c)=2sin(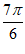 +
+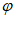 )=-2,
)=-2,
所以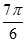 +
+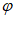 =
=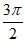 +2k
+2k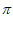 ,k
,k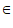 Z,即
Z,即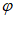 =
=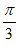 +2k
+2k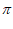 。
。
因为0<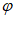 <
<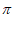 ,所以
,所以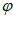 =
=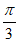 ,k=0。
,k=0。
所以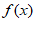 =2sin(2x+
=2sin(2x+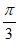 )。
)。
选条件②③:
因为b= ,c=
,c=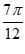 ,所以c-b=
,所以c-b=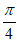 =
=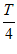 ,即T=
,即T=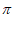 ,则
,则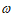 =
=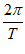 =2。
=2。
由题意可知A=2,则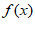 =2sin(2x+
=2sin(2x+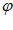 )。
)。
因为c=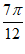 ,
,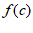 =2sin(
=2sin(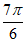 +
+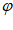 )=-2,
)=-2,
所以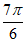 +
+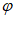 =
=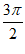 +2k
+2k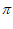 ,k
,k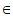 Z,即
Z,即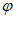 =
=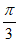 +2k
+2k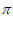 。
。
因为0<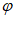 <
<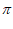 ,所以
,所以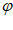 =
=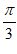 ,k=0。
,k=0。
所以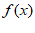 =2sin(2x+
=2sin(2x+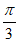 )。
)。
(2)由题意得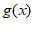 =sin(4x+
=sin(4x+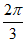 )。
)。
方法一:函数y=sinx的单调递减区间为[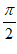 +2k
+2k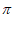 ,
,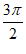 +2k
+2k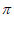 ](k
](k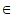 Z)。
Z)。
由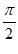 +2k
+2k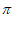 ≤4x+
≤4x+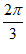 ≤
≤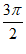 +2k
+2k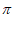 ,
,
得–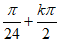 ≤x≤
≤x≤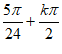 。
。
因为函数y=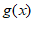 在区间[0,m]上单调递减,且0∈[–
在区间[0,m]上单调递减,且0∈[–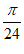 ,
,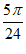 ],此时k=0。
],此时k=0。
所以m≤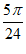 ,所以m的最大值是
,所以m的最大值是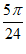 。
。
方法二:因为x∈[0,m],所以4x+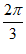
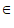 [
[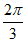 ,4m+
,4m+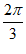 ]。
]。
由题意知y=sint在[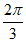 ,4m+
,4m+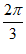 ]上单调递减,
]上单调递减,
所以4m+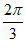 ≤
≤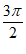 ,
,
所以m≤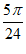 ,所以m的最大值是
,所以m的最大值是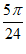 。
。
17. (2019高考全国I文18)
(1)设{an}的公差为d。
由S9=-a5得a1+4d=0。
由a3=4得a1+2d=4。
于是a1=8,d=-2。
因此{an}的通项公式为an=10-2n。
(2)由(1)得a1=-4d,故an=(n-5)d,Sn=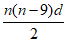 。
。
由a1>0知d<0,故Sn≥an等价于n2-11n+10≤0,解得1≤n≤10。
所以n的取值范围是{n|1≤n≤10,n∈N}。
18. (2022高考全国Ⅱ 18)
(1)因为边长为a的正三角形的面积为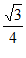 a2,
a2,
所以S1-S2+S3=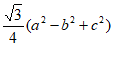 =
=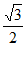 ,即ac cos B=1,
,即ac cos B=1,
由sinB=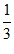 得:cosB=
得:cosB=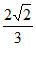 ,所以ac=
,所以ac=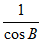 =
=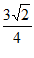 ,
,
故S△ABC=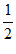 ac sin B=
ac sin B=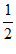 ×
×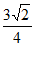 ×
×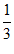 =
=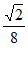 。
。
(2)由正弦定理得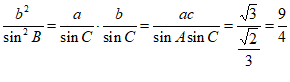 ,
,
故b=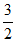 sin B=
sin B=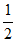 。
。
19. (2022东城高二下期末18)
(1)f(f(-1))=f(2)=22=4。
(2)由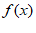 >1,有
>1,有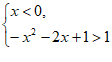 或
或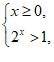
解得x∈(-2,0)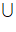 (0,+∞)。
(0,+∞)。
(3)存在唯一的x0=-1,使得f(x0)–f(–x0)=0成立。
20. (2022房山二模19)
(1)当a=0时,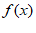 =(x-1)
=(x-1)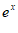 ,
,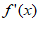 =x
=x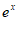 。
。
所以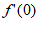 =0,
=0,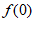 =-1。
=-1。
所以曲线y=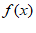 在x=1处的切线方程为y=-1。
在x=1处的切线方程为y=-1。
(2)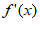 =x
=x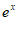 -ax=x(
-ax=x(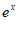 -a)。
-a)。
①当a≤0时,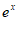 -a>0。
-a>0。
所以x∈[1,2]时,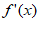 >0。
>0。
所以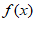 在[1,2]上是增函数。所以
在[1,2]上是增函数。所以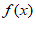 min=f(1)=–
min=f(1)=–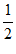 a。
a。
②当a>0时,令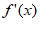 =0,解得x1=lna,x2=0(舍)。
=0,解得x1=lna,x2=0(舍)。
(A)当ln a≤1,即0<a≤e时,x∈[1,2]时,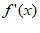 >0。
>0。
所以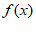 在[1,2]上是增函数。所以
在[1,2]上是增函数。所以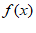 min=f(1)=–
min=f(1)=–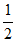 a。
a。
(B)当1<ln a<2,即e<a<c2时,
| (1,ln a) | ln a | (ln a,2) |
| – | 0 | + |
| ↘ | 极小值 | ↗ |
所以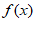 min=f(ln a)=–
min=f(ln a)=–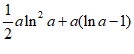 。
。
(C)当ln a≥2,即a≥c2时,x∈[1,2]时,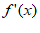 <0。
<0。
所以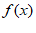 在[1,2]上是减函数。所以
在[1,2]上是减函数。所以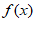 min=f(2)=e2-2a。
min=f(2)=e2-2a。
综上,当a≤e时,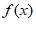 min=–
min=–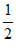 a;
a;
当e<a<e2时,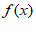 min=–
min=–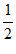 a ln2a+a(lna-1);
a ln2a+a(lna-1);
当a≥e2时,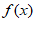 min=e2-2a。
min=e2-2a。
21. (2022西城高三上期末21)
(1)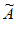 1:1,2,4,7,8;
1:1,2,4,7,8;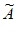 2:1,2,6,7,8;
2:1,2,6,7,8;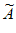 3:1,5,4,7,8;
3:1,5,4,7,8;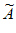 4:1,5,6,7,8。
4:1,5,6,7,8。
(2)依题意,对任意i=2,3,…,N-2,有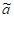 i=ai-1+1或ai+1-1,
i=ai-1+1或ai+1-1,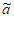 i+1=ai+1或ai+2-1,
i+1=ai+1或ai+2-1,
因为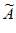 均为递增数列,所以有
均为递增数列,所以有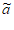 i<
i<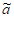 i+1,即同时满足;
i+1,即同时满足;
ai-1+1<ai+1①,ai+1-1<ai+2-1②,ai-1+1<ai+2-1③,ai+1-1<ai+1④。
因为A为递增数列,因此①和②恒成立。
又因为A为整数数列,对于③,ai-1+1≤ai<ai+1≤ai+2-1也恒成立。
对于④,一方面,由ai+1-1<ai+1,得ai+1<ai+2,即ai+1≤ai+1。
另一方面,ai+1≥ai+1,
所以ai+1=ai+1(i=2,3,…,N-2),
即A从第2项到第N-1项是连续的正整数,
所以a2≥a1+1=2,aN-1=a2+N-3≤aN-1=2N-1,因此2≤a2≤N+2,
故a2共有N+1种不同取值,即所有符合条件的数列A共有N+1个。
(3)记bn=an-an-1,依题意,bn∈N*(n=2,3,…,N)。
对任意i=2,3,…,N-1,有ai–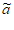 i=bi-1或-bi+1+1,
i=bi-1或-bi+1+1,
注意到0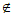 S(
S(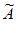 ),即对任意i∈{2,3,…,N-1},有ai–
),即对任意i∈{2,3,…,N-1},有ai–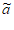 i≠0,
i≠0,
若ai–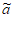 i=bi-1≠0,则bi≠1,即bi≥2;
i=bi-1≠0,则bi≠1,即bi≥2;
若ai–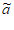 i=-bi+1+1≠0,则bi+1≠1,即bi+1≥2,
i=-bi+1+1≠0,则bi+1≠1,即bi+1≥2,
即对任意i=2,3,…,N-1,或者bi≥2,或者bi+1≥2。
所以bi+bi+1≥3,所以bi-1=-bi+1+1不能成立。
记T1={i|ai–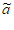 i=bi-1,i=2,3,…,N-1},
i=bi-1,i=2,3,…,N-1},
T2={i|ai–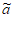 i=-bi+1+1,i=2,3,…,N-1},
i=-bi+1+1,i=2,3,…,N-1},
则T1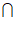 T2=
T2=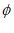 ,且T1
,且T1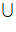 T2={2,3,…,N-1}。
T2={2,3,…,N-1}。
注意到:若存在j∈T2且2≤j≤N-2,即aj–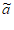 j=-bj+1+1,则j+1∈T2。
j=-bj+1+1,则j+1∈T2。
否则,若j+1∈T1,则aj+1–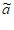 j+1=bj+1-1=–(-bj+1+1)=–(aj–
j+1=bj+1-1=–(-bj+1+1)=–(aj–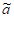 j),不合题意。
j),不合题意。
因此集合T1,T2有以下三种情形:
①T1={2,3,…,N-1},T2=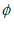 。
。
对任意i∈{2,3,…,N-1},有bi≥2,
则aN=a1+(b2+b3+…+bN-1)+bN≥0+(N-2)·2+1=2N-3,
当且仅当:b2=b3=…=bN-1=2,bN=1,
即A:0,2,4,…,2N-4,2N-3时,等号成立,
此时存在“强紧数列“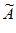 :0,1,3,…,2N-3,
:0,1,3,…,2N-3,
故此情形下,aN的最小值为2N-3;
②T1={2,3,…,k},T2={k+1,k+2,…,N-1},其中k=2,3,…,N-2。
对任意i∈T1,有bi≥2,对任意j∈T2,有bj+1≥2。
aN=a1+(b2+b3+…+bk)+bk+1+(bk+2+bk+3…+bN)
≥0+(k-1)·2+1+(N-k-1)·2=2N-3。
故此情形下,aN的最小值不小于2N-3;
③T1=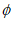 ,T2={2,3,…,N-1}。
,T2={2,3,…,N-1}。
对任意i∈{2,3,…,N-1},有bi+1≥2,
aN=a1+b2+(b3+b4…+bN)≥0+2+(N-2)·2=2N-2>2N-3。
故此情形下,aN的最小值不小于2N-3。
综上,aN的最小值为2N-3。