北京市西城区2020-2021学年下学期初中八年级期末考试数学试卷
本试卷共三道大题,26道小题。满分100分。考试时间100分钟。
一、选择题(本题共30分,每小题3分)
第1—10题均有四个选项,符合题意的选项只有一个.
1.若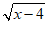 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是
A.x<4 B.x≥4 C.x>4 D.x≥0
2.如图,在□ABCD中,∠C=70°,DE⊥AB于点E,则∠ADE的度数为
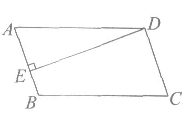
A.30° B.25°
C.20° D.15°
3.下列各式中是最简二次根式的是
A.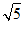 B.
B.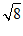 C.
C.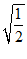 D.
D.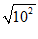
4.下列线段a,b,c组成的三角形中,能构成直角三角形的是
A.a=1,b=2,c=2 B.a=2,b=3,c=4
C.a=3,b=4,c=6 D.a=1,b=1,c=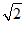
5.在一次学校田径运动会上,参加男子跳高的20名运动员的成绩如下表所示:
成绩/m | 1.55 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 4 | 3 | 4 | 6 | 2 |
这些运动员成绩的众数是
A.1.65 B.1.70 C.1.75 D.1.80
6.如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=4,D是AB边的中点,则CD的长为
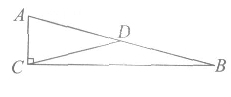
A.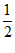 B.2 C.
B.2 C.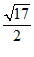 D.
D.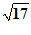
7.下列命题中,正确的是
A.有一组对边相等的四边形是平行四边形
B.有两个角是直角的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直且相等的平行四边形是正方形
8.学校组织校科技节报名,每位学生最多能报3个项目.下表是某班30名学生报名项目个数的统计表:
报名项目个数 | 0 | 1 | 2 | 3 |
人数 | 5 | 14 | a | b |
其中报名2个项目和3个项目的学生人数还未统计完毕,无论这个班报名2个项目和3个项目的学生各有多少人,下列关于报名项目个数的统计量不会发生改变的是
A.中位数,众数 B.平均数,方差 C.平均数,众数 D.众数,方差
9.如图,在平面直角坐标系xOy中,菱形OABC的顶点A的坐标为(0,2),顶点B,C在第一象限,且点C的纵坐标为1,则点B的坐标为
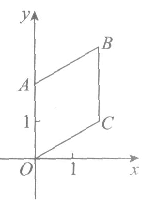
A.(2,3) B.(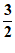 ,3)
,3)
C.(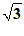 ,
,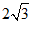 ) D.(
) D.(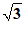 ,3)
,3)
10.如图1,四边形ABCD是平行四边形,连接BD,动点P从点A出发沿折线AB→BD→DA匀速运动,回到点A后停止,设点P运动的路程为x,线段AP的长为y,图2是y与x的函数关系的大致图象,则□ABCD的面积为
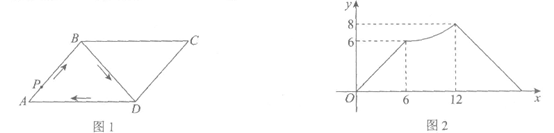
A.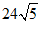 B.
B.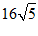 C.
C.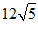 D.36
D.36
二、填空题(本题共21分,第11~15题每小题3分,第16~18题每小题2分)
11.计算: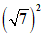 =_______________.
=_______________.
12.已知正方形ABCD的对角线AC的长为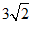 ,则正方形ABCD的边长为_________________.
,则正方形ABCD的边长为_________________.
13.如图,在□ABCD中,对角线AC,BD相交于点O,E是AB的中点,若OE=5,则AD的长为_____________.
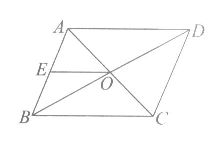
14.已知n是正整数,且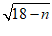 也是正整数,写出一个满足条件的n的值:n=____________.
也是正整数,写出一个满足条件的n的值:n=____________.
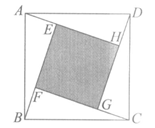
15.如图,在矩形ABCD中,点E在边AD上,EF平分∠AEC交BC于点F.若AD=7,AE=CD=3,则BF的长为_____________.
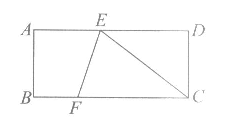
16.用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形,若正方形ABCD的面积为10,AH=3,则正方形EFGH的面积为________________.
17.为了满足不同顾客对保温时效的要求,保温杯生产厂家研发了甲、乙两款保温杯.现从甲、乙两款中各随机抽取了5个保温杯,测得保温时效(单位:h)如下表:
甲组 | 11 | 12 | 13 | 14 | 15 |
乙组 | x | 6 | 7 | 5 | 8 |
如果甲、乙两款保温杯保温时效的方差是相等的,那么x=_______________.
18.如图,点C在线段AB上,△DAC是等边三角形,四边形CDEF是正方形.
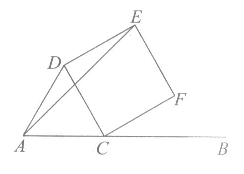
(1) ∠DAE=____________°;
(2)点P是线段AE上的一个动点,连接PB,PC.若AC=2,BC=3,则PB+PC的最小值为________________.
三、解答题(本题共49分,第19~25题每小题6分,第26题7分)
19.计算:(1)
 ; (2)
; (2)
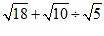 .
.
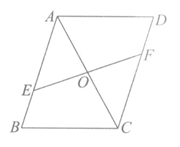
20.如图,在□ABCD中,点E,F分别在边AB,CD上,BE=DF,EF与对角线AC相交于点O.求证:OE=OF.
21.我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何.(1丈=10尺)
大意是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?
将这个实际问题转化为数学问题,根据题意画出图形(如图所示),其中水面宽AB=10尺,线段CD,CB表示芦苇,CD⊥AB于点E.
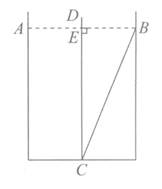
(1)图中DE=__________尺,EB=__________尺;
(2)求水的深度与这根芦苇的长度.
22.在Rt△ABC中,∠ACB=90°,点D是边AB上的一个动点,连接CD.作AE∥DC,CE∥AB,连接ED.
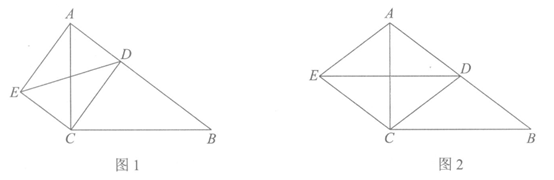
(1)如图1,当CD⊥AB时,求证:AC=ED;
(2)如图2,当D是AB的中点时,
①四边形ADCE的形状是___________;(填“矩形“、“菱形“或“正方形“)
②若AB=10,ED=8,则四边形ADCE的面积为___________________.
23.对于函数y=|x-1|,小芸探究了该函数的部分性质.
下面是小芸的探究过程,请补充完整:
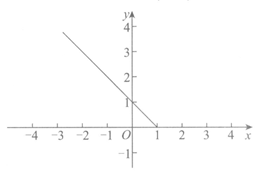
(1)①对于函数y=|x-1|,当x≤1时,y=-x+1;当x>1时,y=_____________;
②当x≤1时,函数y=|x-1|的图象如图所示,请在图中补全函数y=|x-1|的图象;
(2)当y=3时,x=____________;
(3)若点A(-1,y1)和B(x2,y2)都在函数y=|x-1|的图象上,且y2>y1,结合函数图象,直接写出x2的取值范围.
24.某校七年级和八年级学生人数都是200人,学校想了解这两个年级学生的阅读情况,分别从每个年级随机抽取了40名学生进行调查,收集了这80名学生一周阅读时长的数据,并对数据进行了整理、描述和分析.下面给出了部分信息.
a.七、八年级各抽取的40名学生一周阅读时长统计图(不完整)如下(两个年级的数据都分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x<12):
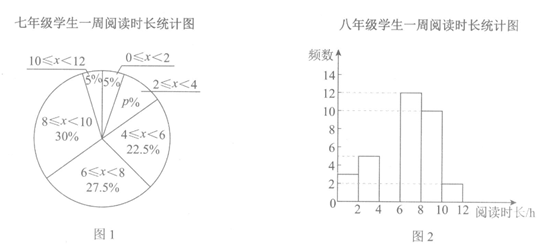
b.八年级学生一周阅读时长在6≤x<8这一组的数据是:
6 6 6 6 6.5 6.5 7 7 7 7 7.5 7.5
c.七、八年级学生一周阅读时长的平均数、中位数和众数如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 6.225 | 7 | 7 |
八年级 | 6.375 | m | 8 |
根据以上信息,回答下列问题:
(1)图1中p%=______________%;
(2)①补全八年级学生一周阅读时长统计图(图2);
②上表中m的值为______________;
(3)将收集的这80名学生的数据分年级由大到小进行排序,其中有一名学生一周阅读时长是6.5小时,排在本年级的前20名,由此可以推断他是__________年级的学生;(填“七“或“八“)
(4)估计两个年级共400名学生中,一周阅读时长不低于8小时的人数.
25.在平面直角坐标系xOy中,点A在x轴的正半轴上,点B在第一象限,作射线OB.给出如下定义:如果点P在∠BOA的内部,过点P作PM⊥OA于点M,PN⊥OB于点N,那么称PM与PN的长度之和为点P关于∠BOA的“内距离“,记作d(P,∠BOA),即d(P,∠BOA)=PM +PN.
(1)如图1,若点P(3,2)在∠BOA的平分线上,则PM=____________,PN=___________,d (P,∠BOA)=___________;
(2)如图2,若∠BOA=75°,点C(a,a)(其中a>0)满足d(C,∠BOA)=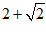 ,求a的值;
,求a的值;
(3)若∠BOA=60°,点Q(m,n)在∠BOA的内部,用含m,n的式子表示d(Q,∠BOA),并直接写出结果.
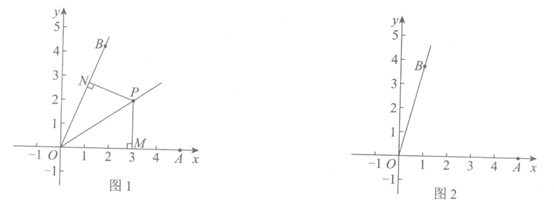
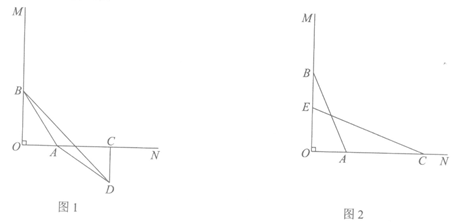
26.已知∠MON=90°,点A是射线ON上的一个定点,点B是射线OM上的一个动点,且满足OB>OA,点C在线段OA的延长线上,且AC=OB.
(1)如图1,CD∥OB,CD=OA,连接AD,BD.
①△AOB与△____全等,∠OBA+∠ADC=_______________°;
②若OA=a,OB=b,则BD=______________;(用含a,b的式子表示)
(2)如图2,在线段BO上截取BE,使BE=OA,连接CE.若∠OBA+∠OCE=β.当点B在射线OM上运动时,β的大小是否会发生变化?如果不变,请求出这个定值;如果变化,请说明理由.
附加题
试卷满分:20分
一、填空题(本题6分)
1.在学习二次根式的过程中,小腾发现有一些特殊无理数之间具有互为倒数的关系.
例如:由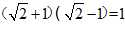 ,可得
,可得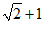 与
与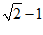 互为倒数,即
互为倒数,即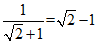 ,
,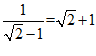 .类似地,
.类似地,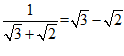 ,
,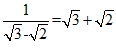 ;
;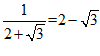 ,
,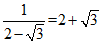 ;….
;….
根据小腾发现的规律,解决下列问题:
(1)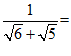 ____________,
____________,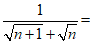 _____________;(n为正整数)
_____________;(n为正整数)
(2)若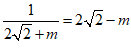 ,则m=____________;
,则m=____________;
(3)计算: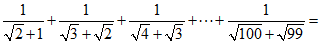 ______________.
______________.
二、解答题(本题共14分,第2题6分,第3题8分)
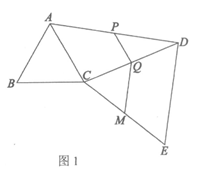
2.如图,△ABC和△DCE都是等边三角形,∠ACD=α(60°<α<120°),点P,Q,M分别是AD,CD,CE的中点.
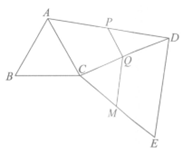
(1)求∠PQM的度数;(用含α的式子表示)
(2)若点N是BC的中点,连接NM,NP,PM,求证:△PNM是等边三角形.
3.在平面直角坐标系xOy中,对于任意两点M(x1,y1),N(x2,y2),我们将|x1-x2|+2|y1-y2|称为点M与点N的“纵2倍直角距离“,记作dMN.
例如:点M(-2,7)与N(5,6)的“纵2倍直角距离“dMN=|-2-5|+2|7-6|=9.
(1)①已知点P1 (1, 1), P2(-4,0), P3(0,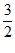 ),则在这三个点中,与原点O的“纵2倍直角距离“等于3的点是____________;
),则在这三个点中,与原点O的“纵2倍直角距离“等于3的点是____________;
②已知点P(x,y),其中y≥0.若点P与原点O的“纵2倍直角距离“dPO=3,请在下图中画出所有满足条件的点P组成的图形;
(2)若直线y=2x+b上恰好有两个点与原点O的“纵2倍直角距离“等于3,求b的取值范围;
(3)已知点A(1,1),B(3,1),点T(t,0)是x轴上的一个动点,正方形CDEF的顶点坐标分别为C(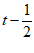 ,0),D(t,
,0),D(t,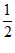 ),E(
),E(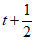 ,0),F(t,
,0),F(t,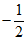 ).若线段AB上存在点G,正方形CDEF上存在点H,使得dGH=5,直接写出t的取值范围.
).若线段AB上存在点G,正方形CDEF上存在点H,使得dGH=5,直接写出t的取值范围.
参考答案
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | A | D | C | C | D | A | D | B |
二、填空题(本题共21分,第11~15题每小题3分,第16~18题每小题2分)
11.7. 12.3. 13.10. 14.答案不唯一,如:9. 15.2.
16.4. 17.4或9. 18.(1) 15;(2) 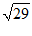 .
.
(说明:第17题答对一个得1分,全对得2分:第18题每空1分)
三、解答题(本题共49分,第19~25题每小题6分,第26题7分)
19.解:(1)
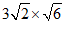
=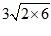 ……………………………….1分
……………………………….1分
=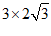 ……………………………………2分
……………………………………2分
=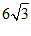 ……………………………3分
……………………………3分
(2)
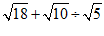
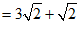 ……………………………2分
……………………………2分
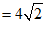 .……………………………3分
.……………………………3分
20.证明:连接EC,AF,如图.
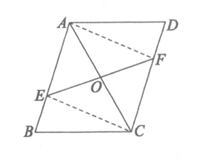
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC. ………………………2分
∵BE=DF,
∴AB-BE=DC-DF,
即AE=FC.
∴四边形AECF是平行四边形, ………………………………4分
∴OE=OF.…………………………………………6分
21.解:(1)1,5; ……………………………………………………2分
(2)设水的深度EC为x尺,则这根芦苇的长CD=CB=(x+1)尺, …………3分
∵CD⊥AB于点E,
∴∠CEB=90°.
∴在Rt△CEB中,CE2+EB2=CB2.
∴x2+52=(x+1)2. …………………………………………………………4分
解得x=12. …………………………………………………5分
则x+1=13. …………………………………………………6分
答:水的深度为12尺,这根芦苇的长度为13尺.
22.(1)证明:∵AE∥DC, CE∥AB,
∴四边形ADCE是平行四边形, …………………………………………2分
∵CD⊥AB,
∴∠ADC=90°.
∴四边形ADCE是矩形, ………………………………………3分
∴AC=ED. ……………………………………………………4分
(2)解:①菱形; …………………………………………………5分
②24. ………………………………………6分
23.解:(1)①x-1; ………………1分
②如图所示; …………………………2分
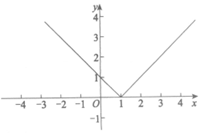
(2) -2或4; ……………………4分
(3)x2<-1或x2>3.……………………6分
24.解:(1)10; ……………………………………2分
(2)①如图所示; ………3分
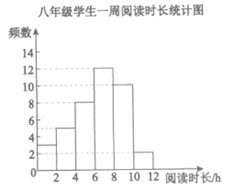
②6.25; ……………………………………4分
(3)八; ………………………………5分
(4) 200×(30%+5%)+200×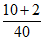 =130(人). …………………………6分
=130(人). …………………………6分
答:估计两个年级一周课外阅读时长不低于8小时的人数约为130人.
25.解:(1)2,2,4; ……………………………………3分
(2)过点C作CD⊥OA于点D,CE⊥OB于点E,连接OC,如图.
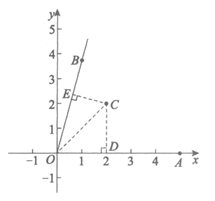
∵点C的坐标为(a,a),
∴CD=OD=a.
∵∠CDO=90°,
∴在Rt△COD中,∠COD=∠OCD=45°,
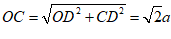 .…………4分
.…………4分
∵∠BOA=75°,
∴∠EOC=∠BOA-∠COD=30°.
∴在Rt△EOC中,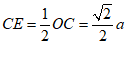 .
.
∵d(C,∠BOA)=CD+CE=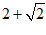 ,
,
∴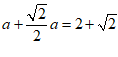 .
.
∴a=2……………………………………5分
(3)
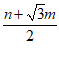 ……………………………………6分
……………………………………6分
26.解:(1)①DCA, …………………………………1分
90; ……………………………………………3分
②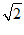 (a+b); …………………………………………4分
(a+b); …………………………………………4分
(2)β的大小不变,
过点C作CF∥OB,且CF=OA,连接AF交CE于点G,连接BF,如图,
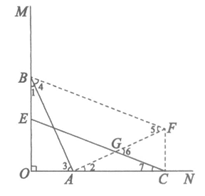
∵CF∥OB,
∴∠BOA+∠ACF=180°.
∵BOA =90°,
∴∠ACF=90°.
∴∠BOA=∠ACF.
在△BOA与△ACF中 ,
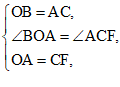
∴△BOA≌△ACF. ………………………………………5分
∴BA=AF, ∠1=∠2.
∴∠4=∠5.
∵∠1+∠3=90°,
∴∠2+∠3=90°.
∴∠BAF=180°-(∠2+∠3) =90°.
∴∠5=45°.
∵BE=OA,
∴BE=CF.
∵BE∥CF,
∴四边形BFCE是平行四边形, ………………………………6分
∴BF∥EC.
∴∠6=∠5=45°.
∵∠1+∠7=∠2+∠7=∠6,
∴∠1+∠7=45°.
即β=45°. ………………………………………………7分
附加题
一、填空题(本题6分)
1.解:(1)
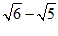 ;………………………………2分
;………………………………2分
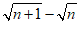 ;…………………………………3分
;…………………………………3分
(2)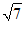 或
或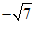 ; …………………………………5分
; …………………………………5分
(3)9. ……………………………6分
二、解答题(本题共14分,第2题6分,第3题8分)
2.(1)解:如图1.
∵Q,M分别是CD,CE的中点,
∴QM∥DE,QM=
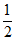 DE.…………………………………1分
DE.…………………………………1分
∴∠CQM=∠CDE.
∵△DCE是等边三角形,
∴∠CDE=60°.
∴∠CQM=60°. …………………………………2分
∵P是AD的中点,
∴PQ∥AC,PQ=
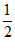 AC.
AC.
∴∠PQC=180°-∠ACD=180°-α.
∴∠PQM=∠PQC+∠CQM=240°-α. …………………………………3分
∴∠PQM=∠PQC+∠CQA=240°-α.………………………………3分
(2)证明:如图2.
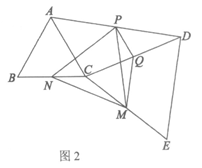
∵△ABC和△DCE都是等边三角形,
∴AC=BC,DE=CE,∠ACB=∠DCE=∠E=60°.
∵N是BC的中点,
∴NC=
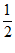 BC=
BC=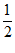 AC.
AC.
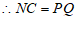
同理 CM=QM.
∵∠NCM=360°-∠ACB -∠ACD-∠DCE=240°-α,
∴∠NCM=∠PQM.…………………………………………4分
在△NCM与△PQM中,
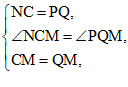
∴△NCM≌△PQM.
∴NM=PM,∠NMC=∠PMQ.……………………………………5分
∴∠NMC+∠CMP=∠PMQ+∠CMP,
即∠NMP=∠CMQ.
∵∠CMQ=∠E=60°,
∴∠NMP=60°.
∴△PNM是等边三角形.…………………………………6分
3.解:(1)①P1, P3; ……………………2分
②如图1所示; …………………………4分
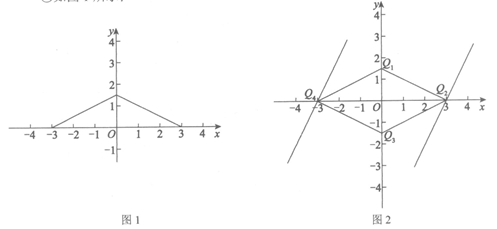
(2)如图2,与原点O的“纵2倍直角距离“等于3的所有点组成的图形是四边形Q1Q2Q3Q4.
当直线y= 2x+b经过点Q2(3,0)时,
0=2×3+b,解得b=-6;
当直线y=2x+b经过点Q4(-3,0)时,
0=2×(-3)+b,解得b=6.
∵直线y=2x+b上恰好有两个点与原点O的“纵2倍直角距离“等于3,
∴b的取值范围是-6<b<6. …………………………………6分
(3)-3≤t≤1或3≤t≤7. ………………………………8分
