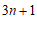北京市石景山区2020-2021学年下学期初中七年级期末考试数学试卷
本试卷共三道大题,28道小题.满分100分,考试时间100分钟.
一、选择题(本题共16分,每小题2分)
下面各题均有四个选项,符合题意的选项只有一个.
1. 如果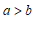 ,那么下列式子一定正确的是
,那么下列式子一定正确的是
A. | B. | C. | D. |
2. 下列运算正确的
A. | B. |
C. | D. |
3. 一粒某种植物花粉的质量约为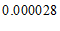 毫克,将
毫克,将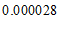 用科学记数法表示应为
用科学记数法表示应为
A. | B. | C. | D. |
4. 如图,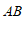 ,
,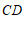 被
被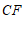 所截,
所截,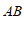 ∥
∥ ,若
,若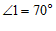 ,则
,则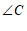 的度数为
的度数为
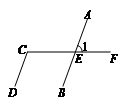
A. | B. |
5. 下列说法正确的是
A.为了了解某品牌汽车的抗撞击情况,适宜采用普查的调查方法 |
B.从 |
C.一组数据的众数有且只有一个 |
D.在统计中,可以用中位数来描述一组数据的集中趋势 |
6. 下列各式从左到右的变形中,是因式分解的为
A. | B. |
C. | D. |
7. 某品牌专营店店主对上一周新进的某款衬衫销售情况统计如下:
尺码 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
平均每天销售数量/件 | 10 | 23 | 30 | 35 | 28 | 21 | 8 |
该店主决定本周进货时,增加一些 码的衬衫,影响该店主决策的统计量是
码的衬衫,影响该店主决策的统计量是
A.平均数 | B.中位数 | C.众数 | D.加权平均数 |
8. 小石将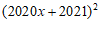 展开后得到多项式
展开后得到多项式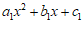 ,小明将
,小明将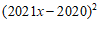 展开后得到多项式
展开后得到多项式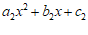 ,若两人计算过程无误,则
,若两人计算过程无误,则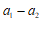 的值为
的值为
A. | B. | C. | D. |
二、填空题(本题共16分,每小题2分)
9. 一个角的余角是这个角的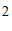 倍,则这个角的度数为
倍,则这个角的度数为
 .
.
10. 如图,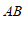 ∥
∥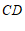 ,
,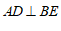 于点
于点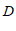 ,
,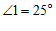 ,则
,则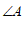 的度数为
的度数为
 .
.
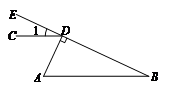
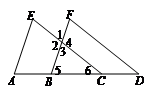
11. 如图,点 ,
, ,
, ,
,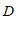 在同一条直线上,若满足条件
在同一条直线上,若满足条件
,则有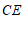 ∥
∥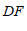 ,理由是
,理由是
.(要求:不再添加辅助线,只需填一个答案即可)
12. 分解因式: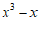 =
=
.
13. 若一组数据 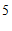 ,
,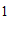 ,
,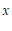 ,
,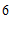 ,
,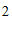 的众数是
的众数是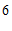 ,则这组数据的中位数是
,则这组数据的中位数是
,平均数是
.
14. 计算: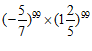 =
=
.
15. 若关于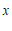 的整式
的整式 能用完全平方公式进行因式分解,则
能用完全平方公式进行因式分解,则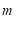 的值是
的值是
.
16.如图所示是一组有规律的图案,它们是由边长相同的正方形与等边三角形镶嵌而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形,第4个图案有13个三角形,…,按照这样的规律,第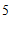 个图案中有
个图案中有
个三角形,第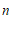 个图案中有
个图案中有
个三角形(用含有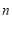 的代数式表示).
的代数式表示).

三、解答题(本题共68分,第17-21题,每小题5分,第22-27题,每小题6分,第28题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算: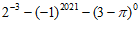 +
+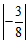 .
.
18.分解因式: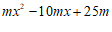 .
.
19.解方程组: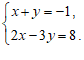
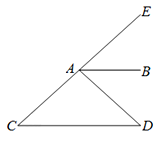
20.如图,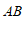 ∥
∥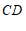 ,
,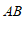 平分
平分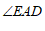 .求证:
.求证: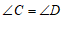 .
.
21.计算: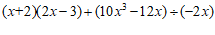 .
.
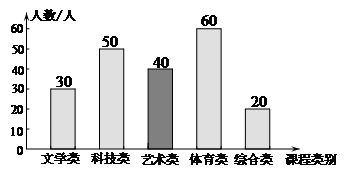
22.为了满足学生的多元文化需求,促进学生身心健康和谐发展,某校准备开展形式多样的特色课程.为了了解学生对部分课程的喜爱程度,学校对该校部分学生进行了一次”你最喜爱的特色课程”的问卷调查(每个被调查的学生必须选择而且只能选择其中一项),并将调查结果绘制成了如下两幅统计图(不完整):
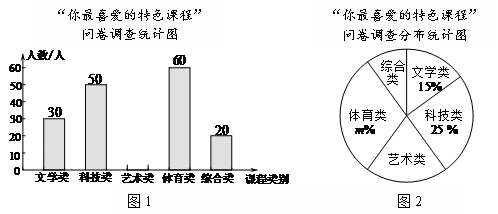
请根据统计图提供的信息,完成下列问题:
(1)此次被调查的学生共有
人;
(2)请将上面统计图1补充完整并在图上标出数据;
(3)统计图2中,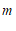 =
=
;”综合类”部分扇形的圆心角是
 ;
;
(4)若该校共有学生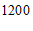 人,根据调查结果估计该校最喜欢”科技类”特色课程的学生约有
人,根据调查结果估计该校最喜欢”科技类”特色课程的学生约有
人.
23.解不等式组: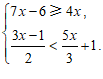
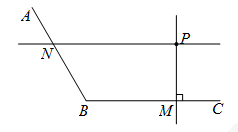
24.如图,点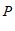 为
为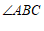 内一点.
内一点.
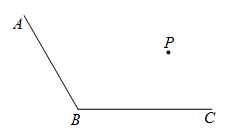
(1)画图:①过点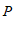 画
画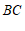 的垂线,垂足为点
的垂线,垂足为点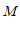 ;
;
②过点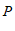 画
画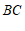 的平行线,交
的平行线,交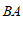 于点
于点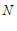 ;
;
(2)若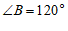 ,则
,则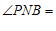
 ,理由是
,理由是
.
25.已知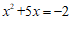 ,求代数式
,求代数式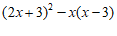 的值.
的值.
26.列一元一次不等式解应用题:
某校七年级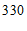 名师生外出参加社会实践活动,租用
名师生外出参加社会实践活动,租用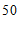 座与
座与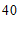 座的两种客车.如果
座的两种客车.如果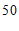 座的客车租用了
座的客车租用了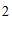 辆,那么至少需要租用多少辆
辆,那么至少需要租用多少辆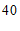 座的客车?
座的客车?
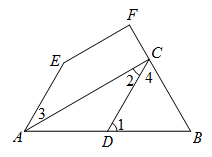
27.如图,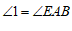 ,
,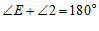 .
.
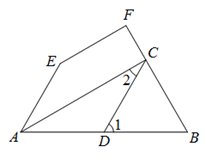
(1)判断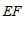 与
与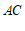 的位置关系,并证明;
的位置关系,并证明;
(2)若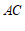 平分
平分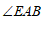 ,
,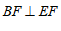 于点
于点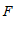 ,
,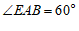 ,求
,求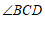 的度数.
的度数.
28.对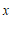 ,
,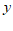 定义一种新运算
定义一种新运算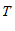 ,规定
,规定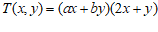 ,其中
,其中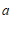 ,
,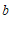 是非零常数,等式右边是通常的四则运算.
是非零常数,等式右边是通常的四则运算.
如: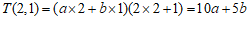 ,
,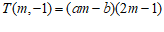 .
.
(1)填空: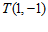 =
=
(用含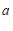 ,
,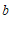 的代数式表示);
的代数式表示);
(2)已知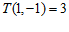 且
且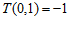 .
.
①求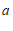 ,
,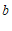 的值;
的值;
②若关于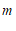 的不等式组
的不等式组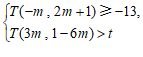 恰好有三个整数解,求
恰好有三个整数解,求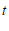 的取值范围.
的取值范围.
(3)当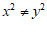 时,
时,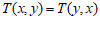 对任意的有理数
对任意的有理数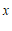 ,
,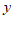 都成立,请直接写出
都成立,请直接写出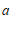 ,
,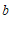 满足的关系式.
满足的关系式.
【试题答案】
阅卷须知:
1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可.
2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.
3.评分参考中所注分数,表示考生正确做到此步应得的累加分数.
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | C | C | D | D | C | B |
二、填空题(本题共16分,每小题2分)
9. | 10. | |
11.答案不唯一,如: | ||
12. | 13. | 14. |
15. | 16. | |
三、解答题(本题共68分,第17-21题,每小题5分,第22-27题,每小题6分,第28题7分)解答应写出文字说明、演算步骤或证明过程.
17.解:原式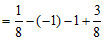 ………………………… 4分
………………………… 4分
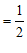 . ………………………… 5分
. ………………………… 5分
18.解:原式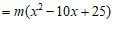
………………………… 2分
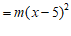 . ………………………… 5分
. ………………………… 5分
 19.解方程组:
19.解方程组: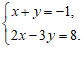
解:①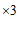 ,得
,得 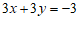 . ③ ………………………… 2分
. ③ ………………………… 2分
③+②,得 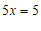 .
.
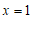 . ………………………… 3分
. ………………………… 3分
把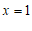 代入①,得
代入①,得 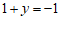 .
.
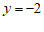 . ………………………… 4分
. ………………………… 4分
∴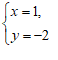 是原方程组的解. ………………………… 5分
是原方程组的解. ………………………… 5分
20.证明:∵ 平分
平分 (已知),
(已知),
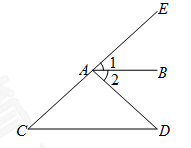
∴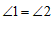 (角平分线定义). …………… 1分
(角平分线定义). …………… 1分
∵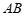 ∥
∥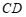 (已知),
(已知),
∴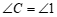 (两直线平行,同位角相等),
(两直线平行,同位角相等),
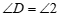 (两直线平行,内错角相等).………………………… 4分
(两直线平行,内错角相等).………………………… 4分
∴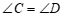 (等量代换). ………………………… 5分
(等量代换). ………………………… 5分
21.解:原式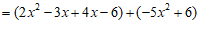 ………………………… 2分
………………………… 2分
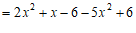 ………………………… 4分
………………………… 4分
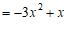 . ………………………… 5分
. ………………………… 5分
22.解:(1)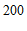 ; ………………………… 1分
; ………………………… 1分
(2)如图所示; ………………………… 3分
(3) ;
;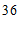 ; ………………………… 5分
; ………………………… 5分
(4)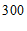 . ………………………… 6分
. ………………………… 6分
 23.解不等式组:
23.解不等式组: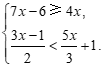
解:解不等式①,得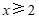 . ………………………… 2分
. ………………………… 2分
解不等式②,得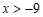 . ………………………… 5分
. ………………………… 5分
∴原不等式组的解集为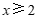 . ………………………… 6分
. ………………………… 6分
24.解:(1)如图所示; ………………………… 4分
(2) , ………………………… 5分
, ………………………… 5分
两直线平行,同旁内角互补. ………………………… 6分
25.解:原式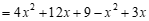 ………………………… 2分
………………………… 2分
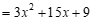 . ………………………… 3分
. ………………………… 3分
∵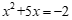 ,
,
∴原式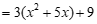 ………………………… 5分
………………………… 5分
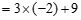
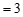 . ………………………… 6分
. ………………………… 6分
26.解:设需要租用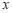 辆
辆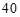 座的客车,根据题意,得 ………………………… 1分
座的客车,根据题意,得 ………………………… 1分
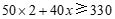 . ………………………… 4分
. ………………………… 4分
解这个不等式,得 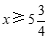 . ………………………… 5分
. ………………………… 5分
由于客车是按辆计算的,所以符合题意的解只能取整数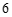 .
.
答:至少需要租用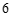 辆
辆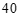 座的客车. ………………………… 6分
座的客车. ………………………… 6分
27.解:(1)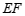 与
与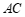 的位置关系是
的位置关系是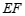 ∥
∥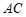 . ………………………… 1分
. ………………………… 1分
证明:
∵ (已知),
(已知),
∴ ∥
∥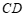 (同位角相等,两直线平行).
(同位角相等,两直线平行).
∴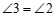 (两直线平行,内错角相等).
(两直线平行,内错角相等).
∵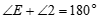 (已知),
(已知),
∴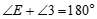 (等量代换).
(等量代换).
∴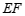 ∥
∥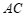 (同旁内角互补,两直线平行). ………………………… 3分
(同旁内角互补,两直线平行). ………………………… 3分
(2)∵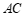 平分
平分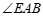 ,
,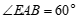 (已知),
(已知),
∴ (角平分线定义).
(角平分线定义).
∴ (等量代换).
(等量代换).
∵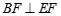 (已知),
(已知),
∴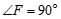 (垂直定义).
(垂直定义).
∵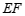 ∥
∥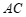 (已证),
(已证),
∴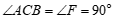 (两直线平行,同位角相等).
(两直线平行,同位角相等).
∴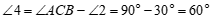 . ………………………… 6分
. ………………………… 6分
28.解:(1)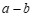 ; ………………………… 1分
; ………………………… 1分
(2)①∵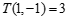 且
且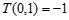 ,
,
∴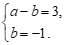
解得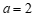 ,
,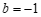 . ………………………… 3分
. ………………………… 3分
②由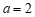 ,
,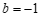 ,可得
,可得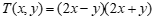 .
.
∴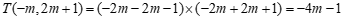 ,
,
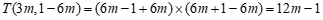 .
.
则不等式组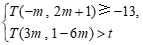 即为不等式组
即为不等式组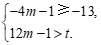
解得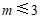 且
且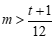 .
.
∵原不等式组恰好有三个整数解,
∴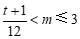 ,其中
,其中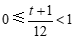 .
.
∴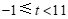 . ………………………… 6分
. ………………………… 6分
(3)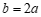 . ………………………… 7分
. ………………………… 7分

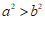
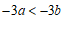
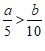
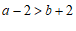
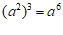
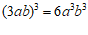
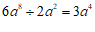
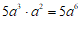
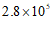
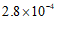
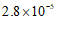
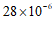
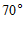
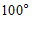 C.
C.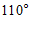 D.
D.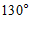
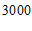 名学生中随机抽取
名学生中随机抽取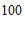 名学生进行调查,样本容量是
名学生进行调查,样本容量是 名学生
名学生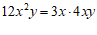
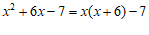
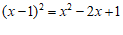
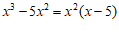
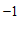
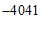
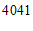
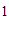
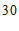
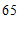
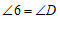 ;同位角相等,两直线平行
;同位角相等,两直线平行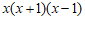
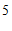 ;
;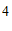
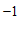
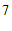 或
或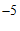
 ;
;