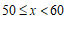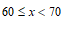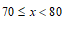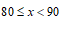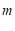北京市海淀区2020-2021学年下学期初中八年级期末学业水平调研数学试卷
本试卷共3道大题,25道小题,满分100分;考试时长90分钟。
一、选择题(本题共30分,每小题3分)
在下列各题的四个选项中,只有一个是符合题意的.
1.计算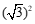 的结果为
的结果为
A. | B. | C. | D. |
2.以下列长度的三条线段为边,能组成直角三角形的是
A. | B. | C. | D. |
3.将直线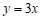 向下平移
向下平移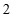 个单位长度后,得到的直线是
个单位长度后,得到的直线是
A. | B. | C. | D. |
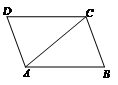
4.如图,在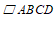 中,
中,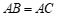 ,
,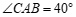 ,则
,则 的度数是
的度数是
A. | B. |
5.一家鞋店在一段时间内销售了某种女鞋40双,各种尺码的鞋的销售量如下表所示:
尺码/cm | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
销售量/双 | 1 | 2 | 5 | 7 | 14 | 8 | 3 |
店主再进一批女鞋时,打算多进尺码为24 cm的鞋,你认为他做这个决定是重点关注了下列统计量中的
A.平均数 | B.中位数 | C.众数 | D.方差 |
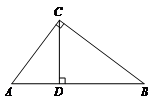
6.如图,在 中,
中,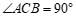 ,
,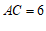 ,
,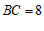 ,则
,则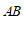 边上的高
边上的高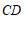 的长为
的长为
A. | B. |
7.如图,一次函数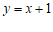 与
与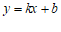 的图象交于点
的图象交于点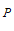 ,则关于
,则关于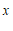 ,
,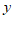 的方程组
的方程组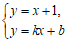 的解是
的解是
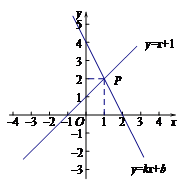
A. | B. |
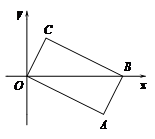
8.如图,在平面直角坐标系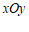 中,矩形
中,矩形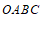 的顶点
的顶点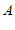 ,
,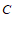 的坐标分别是
的坐标分别是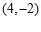 ,
,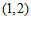 ,点
,点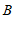 在
在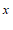 轴上,则点
轴上,则点 的横坐标是
的横坐标是
A.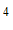 B.
B.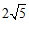 C.
C.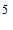 D.
D.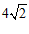
9.如图,在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出1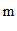 ,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5
,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部5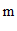 ,由此可计算出学校旗杆的高度是
,由此可计算出学校旗杆的高度是

A.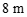 B.
B.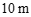 C.
C.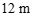 D.
D.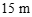
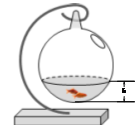
10.如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度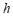 、水面的面积
、水面的面积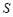 及注水量
及注水量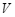 是三个变量.下列有四种说法:
是三个变量.下列有四种说法:
①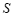 是
是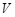 的函数; ②
的函数; ②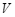 是
是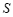 的函数;
的函数;
③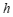 是
是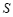 的函数; ④
的函数; ④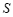 是
是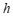 的函数.
的函数.
其中所有正确结论的序号是
A.①③ B.①④ C.②③ D.②④
二、填空题(本题共18分,每小题3分)
11.若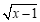 在实数范围内有意义,则实数
在实数范围内有意义,则实数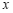 的取值范围是________.
的取值范围是________.
12.函数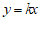 (
(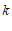 是常数,
是常数,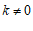 )的图象上有两个点
)的图象上有两个点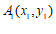 ,
,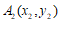 ,当
,当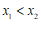 时,
时,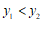 ,写出一个满足条件的函数解析式:________.
,写出一个满足条件的函数解析式:________.
13.如图,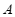 ,
,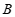 两点被池塘隔开,在
两点被池塘隔开,在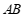 外选一点
外选一点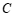 ,连接
,连接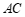 和
和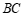 .分别取
.分别取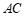 ,
,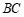 的中点
的中点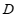 ,
,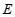 ,测得
,测得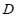 ,
,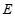 两点间的距离为
两点间的距离为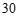
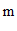 ,则
,则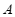 ,
, 两点间的距离为________
两点间的距离为________ .
.
14.一个水库的水位在最近5h 内持续上涨,下表记录了这5h 内6个时间点的水位高度,其中t 表示时间,y 表示水位高度.
t/h | 0 | 1 | 2 | 3 | 4 | 5 |
y/m | 3 | 3.3 | 3.6 | 3.9 | 4.2 | 4.5 |
据估计这种上涨规律还会持续2h,预测再过2h 水位高度将为________ m.
15.在平面直角坐标系 中,直线
中,直线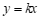 (
(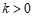 )与直线
)与直线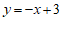 ,直线
,直线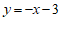 分别交于
分别交于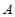 ,
,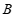 两点.若点
两点.若点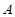 ,
,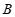 的纵坐标分别为
的纵坐标分别为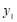 ,
,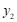 ,则
,则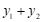 的值为________.
的值为________.
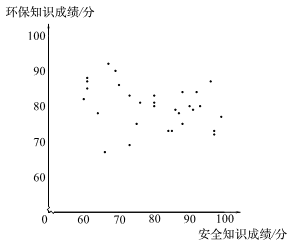
16.某校八年级有600名学生,为了解他们对安全与环保知识的认识程度,随机抽取了30名学生参加安全与环保知识问答活动.此活动分为安全知识和环保知识两个部分.这30名学生的安全知识成绩和环保知识成绩如图所示.根据下图,判断安全知识成绩的方差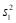 和环保知识成绩的方差
和环保知识成绩的方差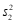 的大小:
的大小: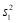 ________
________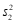 (填”>”,”=”或”<“).
(填”>”,”=”或”<“).
三、解答题(本题共52分,第17题8分,第18-23题,每小题5分,第24-25题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:(1)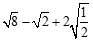 ; (2)
; (2)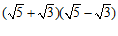 .
.
18.如图,在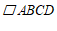 中,点
中,点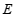 ,
,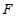 分别在
分别在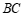 ,
,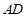 上,且
上,且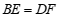 ,连接
,连接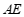 ,
,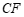 .
.
求证: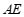 //
//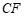 .
.
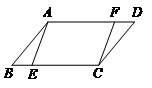
19.下面是小明设计的”过直线外一点作已知直线的平行线”的尺规作图过程.
已知:如图1,直线l 及直线l 外一点A.
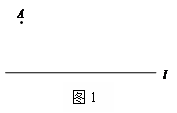
求作:直线AD,使得AD// l.
作法:如图2,
①在直线l 上任取两点B,C,连接AB;
②分别以点A,C 为圆心,线段BC,AB 长为半径画弧,两弧在直线l 上方相交于点D;
③作直线AD.
直线AD 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接CD.
∵ AB =________,BC =________,
∴ 四边形ABCD 为平行四边形(_____________________)(填推理的依据).
∴ AD// l.
20.在平面直角坐标系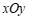 中,一次函数的图象经过点
中,一次函数的图象经过点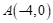 与
与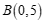 .
.
(1)求这个一次函数的解析式;
(2)若点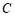 是
是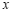 轴上一点,且
轴上一点,且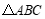 的面积是5,求点
的面积是5,求点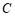 的坐标.
的坐标.
21.如图,在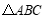 中,
中,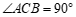 ,
,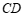 为边
为边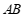 上的中线,点
上的中线,点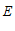 与点
与点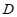 关于直线
关于直线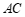 对称,连接
对称,连接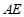 ,
,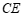 .
.
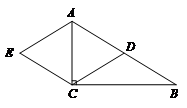
(1)求证:四边形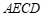 是菱形;
是菱形;
(2)连接BE,若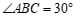 ,
,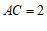 ,求
,求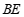 的长.
的长.
22.第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在中国北京和张家口市联合举行.为了解学生对冬奥会冰雪项目的认识程度,某校体育组老师从该校八年级学生中随机抽取了20名学生进行冰上项目和雪上项目的知识测试,获得了他们的测试成绩(百分制),并对数据(测试成绩)进行整理、描述和分析.下面给出了部分信息.
a.测试成绩的频数分布表如下:
项目 |
|
|
|
|
|
冰上项目 | 0 | 0 | 12 | 6 | 2 |
雪上项目 | 1 | 4 | 7 | 3 | 5 |
b.雪上项目测试成绩在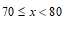 这一组的是:
这一组的是:
70707071717375
c.冰上项目和雪上项目测试成绩的平均数、中位数、众数如下:
项目 | 平均数 | 中位数 | 众数 |
冰上项目 | 77.95 | 76 | 75 |
雪上项目 | 76.85 |
| 70 |
根据以上信息,回答下列问题:
(1)表中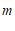 的值为__________;
的值为__________;
(2)在此次测试中,某学生的冰上项目测试成绩为75分,雪上项目测试成绩为73分,这名学生测试成绩排名更靠前的是__________(填”冰上”或”雪上”)项目,理由是________________________________________;
(3)已知该校八年级共有200名学生,假设该年级学生都参加此次测试,估计冰上项目测试成绩不低于80分的人数.
23.在平面直角坐标系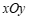 中,直线
中,直线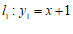 与直线
与直线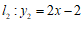 交于点
交于点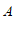 .
.
(1)求点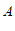 的坐标;
的坐标;
(2)当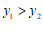 时,直接写出
时,直接写出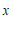 的取值范围;
的取值范围;
(3)已知直线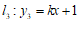 ,当
,当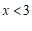 时,对于
时,对于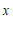 的每一个值,都有
的每一个值,都有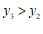 ,直接写出
,直接写出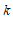 的取值范围.
的取值范围.
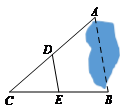
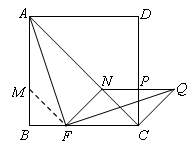
24.在正方形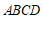 中,
中,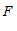 是线段
是线段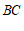 上一动点(不与点
上一动点(不与点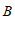 ,
,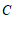 重合),连接
重合),连接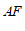 ,
,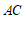 ,分别过点
,分别过点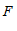 ,
,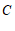 作
作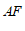 ,
,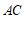 的垂线交于点
的垂线交于点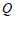 .
.
(1)依题意补全图1,并证明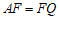 ;
;
(2)过点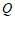 作
作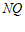 ∥
∥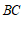 ,交
,交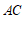 于点
于点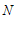 ,连接
,连接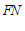 .若正方形
.若正方形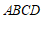 的边长为1,写出一个
的边长为1,写出一个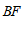 的值,使四边形
的值,使四边形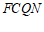 为平行四边形,并证明.
为平行四边形,并证明.
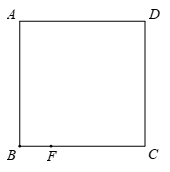
图1 备用图
25.在平面直角坐标系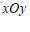 中,对于点
中,对于点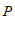 与
与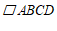 ,给出如下的定义:
,给出如下的定义:
将过点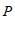 的直线记为
的直线记为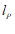 ,若直线
,若直线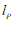 与
与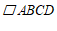 有且只有两个公共点,则称这两个公共点之间的距离为直线
有且只有两个公共点,则称这两个公共点之间的距离为直线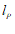 与
与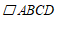 的”穿越距离”,记作
的”穿越距离”,记作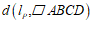 .
.
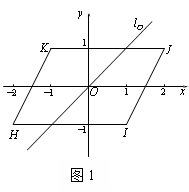
例如,已知过点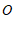 的直线
的直线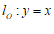 与
与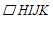 ,其中
,其中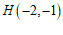 ,
,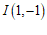 ,
,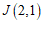 ,
,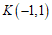 ,如图1所示,则
,如图1所示,则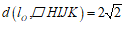 .
.
请解决下面的问题:
已知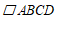 ,其中
,其中 ,
,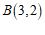 ,
,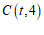 ,
,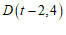 .
.
(1)当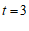 时,已知
时,已知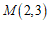 ,
,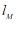 为过点
为过点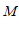 的直线
的直线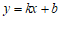 .
.
①当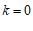 时,
时,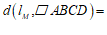 ________________;
________________;
当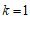 时,
时,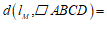 ________________;
________________;
②若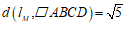 ,结合图象,求
,结合图象,求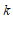 的值;
的值;
(2)已知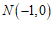 ,
,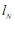 为过点
为过点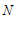 的直线,若
的直线,若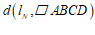 有最大值,且最大值为
有最大值,且最大值为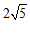 ,直接写出
,直接写出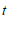 的取值范围.
的取值范围.
【试题答案】
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | C | B | D | C | B | A | C | C | B |
二、填空题(本题共18分,每小题3分)
11.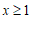 ; 12.
; 12.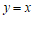 (答案不唯一); 13.
(答案不唯一); 13.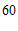 ; 14.
; 14.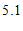 ; 15.0; 16.
; 15.0; 16.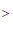 .
.
三、解答题(本题共52分,第17题8分,第18-23题每小题5分,第24-25题每小题7分)
17.解:(1)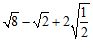 ;
;
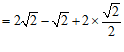 ………………………2分
………………………2分
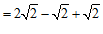 ………………………3分
………………………3分
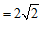 ………………………4分
………………………4分
(2)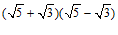 .
.
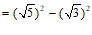 ………………………1分
………………………1分
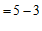 ………………………3分
………………………3分
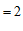 ………………………4分
………………………4分
18.证明:∵四边形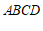 是平行四边形,
是平行四边形,
∴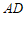 ∥
∥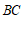 ,
,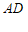 =
=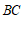 . ………………………2分
. ………………………2分
∵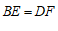 ,
,
∴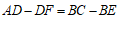 .
.
即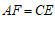 . ………………………3分
. ………………………3分
又∵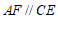 ,
,
∴四边形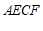 是平行四边形. ………………………4分
是平行四边形. ………………………4分
∴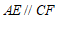 . ………………………5分
. ………………………5分
19.(1)
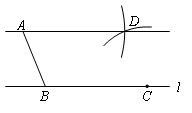
………………………2分
(2)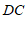 ,
,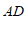 ………………………4分
………………………4分
两组对边分别相等的四边形是平行四边形. ………………………5分
20.(1)解:设这个一次函数的解析式为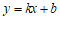 (
(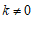 ). ……………………1分
). ……………………1分
∵一次函数的图象经过点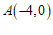 与
与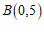 ,
,
∴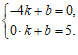 ………………………2分
………………………2分
∴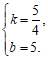
∴这个一次函数的解析式为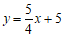 . ………………………3分
. ………………………3分
(2)解:设点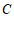 的坐标为
的坐标为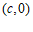 (
(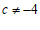 ).
).
∵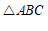 的面积是5,
的面积是5,
∴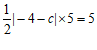 .
.
∴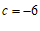 或
或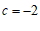 .
.
∴点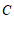 的坐标为
的坐标为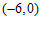 或
或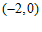 . ………………………5分
. ………………………5分
21.(1)证明:
∵点E与点D关于直线AC对称,
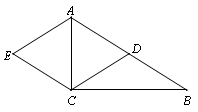
∴CE=CD,AE=AD. ………………………1分
∵∠ACB=90°,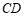 为边
为边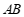 上的中线,
上的中线,
∴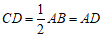 . ………………………2分
. ………………………2分
∴CE=CD=AD=AE.
∴四边形AECD是菱形. ………………………3分
(2)过E作EN⊥BC交BC的延长线于点N.
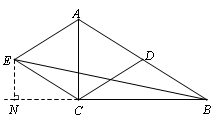
在△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴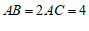 .
.
∴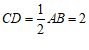 .
.
由勾股定理得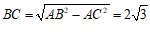 .
.
∵四边形AECD是菱形,
∴EC=CD=2,EC//AD.
∴∠ECN=30°.
∵∠ENC=90°,
∴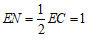 .
.
由勾股定理得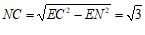 . ………………………4分
. ………………………4分
∴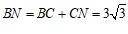 .
.
∵∠ENC=90°,
由勾股定理得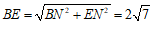 . ………………………5分
. ………………………5分
22.(1)72; ………………………1分
(2)雪上; ………………………2分
这名学生的冰上项目测试成绩是75分,小于中位数76分,所以该生冰上项目的成绩在10名以后;这名学生的雪上项目测试成绩是73分,大于中位数72分,所以该生冰上项目的成绩在10名以前,所以这名学生的雪上项目成绩排名更靠前. ……………………3分
(3)在样本中,冰上项目测试成绩在组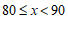 ,
,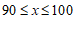 的人数分别为6,2,所以样本中冰上项目测试成绩不低于80分的人数为8人.
的人数分别为6,2,所以样本中冰上项目测试成绩不低于80分的人数为8人.
假设该年级学生都参加此次测试,估计冰上项目测试成绩不低于80分的人数为
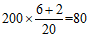 . ………………………5分
. ………………………5分
23.(1)解:由题可知,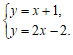 ………………………1分
………………………1分
解得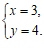
∴点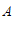 的坐标是
的坐标是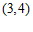 . ………………………2分
. ………………………2分
(2)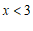 ; ………………………3分
; ………………………3分
(3)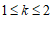 . ………………………5分
. ………………………5分
24.(1)补全图形如图所示:
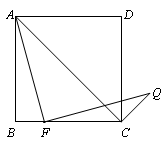
………………………1分
证明:如图,在BA上截取BM=BF,连接MF.
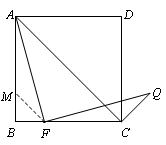
∵四边形ABCD为正方形,
∴AB=BC,∠B=∠BCD=90°,AC平分∠BCD.
∴∠ACB=45°. ………………………2分
∵CQ⊥AC,
∴∠ACQ =90°.
∴∠FCQ=∠ACB+∠ACQ=135°.
∵BM=BF,∠B=90°,
∴∠FMB=∠MFB=45°,
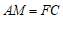 . ①
. ①
∴∠AMF =180°-∠FMB=135°.
∴∠AMF =∠FCQ. ② ………………………3分
∵FQ⊥AF,
∴∠AFQ=90°.
∴∠QFC +∠AFB =90°.
∵∠B =90°,
∴∠BAF +∠AFB =90°.
∴∠BAF=∠CFQ. ③
由①②③得△AMF≌△FCQ.
∴AF=FQ. ………………………4分
(2)当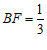 时,四边形FCQN为平行四边形. ………………………5分
时,四边形FCQN为平行四边形. ………………………5分
证明:如图,在BA上截取BM=BF,连接MF.
∵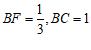 ,
,
∴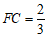 .
.
由(1)可得△BMF为等腰直角三角形,且△AMF≌△FCQ.
∴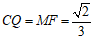 . ………………………6分
. ………………………6分
∵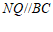 ,
,
∴∠FCQ +∠NQC =180°.
∵∠FCQ =135°,
∴∠NQC =45°.
∵∠NCQ =90°,
∴∠NQC =45°=∠NQC.
∴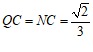 .
.
∴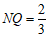 .
.
∴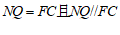 .
.
∴四边形FCQN为平行四边形. ………………………7分
25.(1)①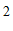 ; ………………………1分
; ………………………1分
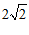 . ………………………2分
. ………………………2分
②解:∵直线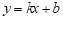 过点
过点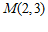 ,
,
∴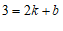 .
.
∴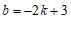 .
.
∴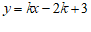 .
.
如图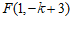 ,
,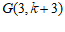 .
.
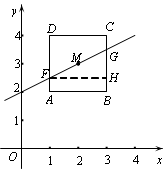
过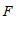 作
作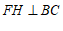 于
于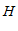 ,则
,则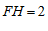 .
.
∵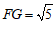 ,
,
∴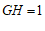 .
.
∴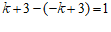 .
.
∴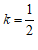 .
.
结合图象,由正方形的轴对称性可知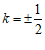 ,
,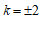 均符合题意. …5分
均符合题意. …5分
(2)t的取值范围是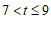 . ………………………7分
. ………………………7分

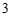
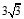
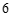
 ,
, ,
,
 ,
, ,
,
 ,
,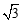 ,
,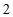
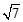 ,
,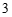 ,
,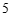
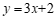
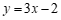
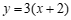
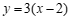
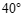
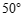 C.
C.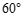 D.
D.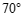
 C.
C. D.
D.
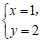
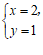 C.
C.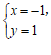 D.
D.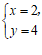
 /分
/分