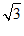北京市朝阳区2020-2021学年下学期初中八年级期末学业水平调研数学试卷
本试卷共25道小题,满分100分,闭卷考试,时间90分钟。
一、选择题(本题共24分,每小题3分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.下列二次根式中,最简二次根式是
A.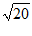 B.
B.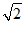 C.
C.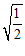 D.
D.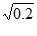
2.以下列各组数为边长,可以构成直角三角形的是
A.5,12,13 B.1,2,3 C.3,3,3 D.4,5,6
3.一个菱形的两条对角线的长度分别是6 cm和8 cm,这个菱形的面积是
A.12 cm2 B.14 cm2 C.24 cm2 D.48 cm2
4.下列计算正确的是
A.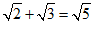 B.
B.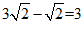
C.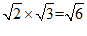 D.
D.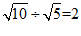
5.对八年级500名学生某次数学检测的成绩(百分制)进行了两次统计,第一次统计时,系统把一位缺考同学的成绩自动填充为该次检测唯一的零分,第二次统计时,老师删去了这个零分,则以下统计量在这两次统计中一定保持不变的是
A.平均数 B.众数 C.中位数 D.方差
6.若四边形ABCD是 甲 ,则四边形ABCD一定是 乙 ,甲、乙两空可以填
A.平行四边形,矩形 B.矩形,菱形
C.菱形,正方形 D.正方形,平行四边形
7.如图,A,B为 的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出
的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出
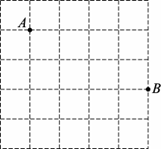
A.1个 B.2个 C.3个 D.4个
8.如图,中国国家博物馆收藏了元代制作的计时工具”铜壶滴漏”,这是目前发现形制最大、最完备的一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四个铜壶依次名为”日壶”、”月壶”、”星壶”、”受水壶”,通过多级滴漏,使得”星壶”中的水可以匀速滴入圆柱形的”受水壶”中,”受水壶”中带有刻度的木箭随着水位匀速上移,对准标尺就能读出相应的时间.在一天中,”受水壶”中的水面高度h与时间t的函数图象可能是


二、填空题(本题共24分,每小题3分)
9.若二次根式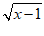 在实数范围内有意义,则实数x的取值范围是
在实数范围内有意义,则实数x的取值范围是
.
10.请写出一个y随x的增大而减小的正比例函数的表达式:
.
11.为了庆祝中国共产党成立100周年,加深同学们对中国共产党历史的认识,激发爱党、爱国热情,某班举行了党史知识竞赛,成绩统计如下表,这组数据的中位数是
.
成绩(百分制) | 80 | 85 | 90 | 95 | 100 |
人数 | 1 | 2 | 5 | 21 | 6 |
12.一位求职者参加某公司的招聘,面试和笔试的成绩分别是86和90,公司给出他这两项测试的平均成绩为87.6,可知此次招聘中
(填”面试”或”笔试”)的权重较大.
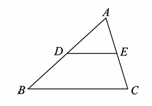
13.如图,在△ABC中,D,E分别为AB,AC边的中点,若DE=3,则BC的长为
.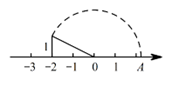
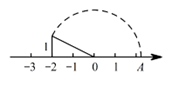
14.如图,一次函数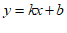 的图象经过点A(1,2),关于x的不等式
的图象经过点A(1,2),关于x的不等式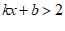 的解集为
的解集为
.
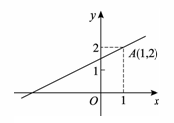
15.如图,菱形ABCD的对角线AC,BD相交于点O,P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AB=4,∠BAD=60°,则EF的最小值为
.
16.若直线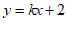 与两条坐标轴围成的三角形的面积是2,则k的值为
与两条坐标轴围成的三角形的面积是2,则k的值为
.
三、解答题(本题共52分,17-22题,每小题5分,第23题7分,第24题7分,第25题8分)
17.计算: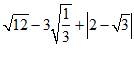 .
.
18.已知:∠AOB.
求作:∠AOB的平分线.
作法:①以点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D;
②分别以点C,D为圆心,OC长为半径画弧,两弧在∠AOB的内部相交于点P;
③画射线OP.
射线OP即为所求.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接PC,PD.
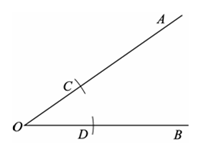
由作法可知OC=OD=PC=PD.
∴四边形OCPD是
.
∴OP平分∠AOB(
)(填推理的依据).
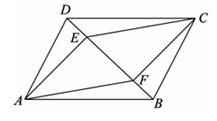
19.如图,在□ABCD中,E,F是对角线BD上的两点,且DE=BF.
求证:四边形AECF是平行四边形.
20.一次函数的图象经过点(-1,0)和(0,2).
(1)求这个一次函数的表达式;
(2)若直线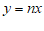 与该一次函数的图象相交,且交点在第三象限,直接写出n的取值范围.
与该一次函数的图象相交,且交点在第三象限,直接写出n的取值范围.
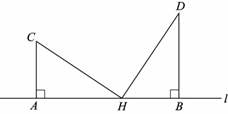
21.如图,A,B,H是直线l上的三个点,AC⊥l于点A,BD⊥l于点B,且HC=HD,AB=5,AC=2,BD=3,求AH的长.
22.在2020年开展的第七次全国人口普查,是在中国特色社会主义进入新时代开展的重大国情国力调查,全面查清中国人口数量、结构、分布、城乡住房等方面的情况,为开启全面建设社会主义现代化国家新征程,向第二个百年奋斗目标进军,提供科学准确的统计信息支持.
下面给出了本次调查公布的部分数据:
a.图1为2010年(第六次)、2020年(第七次)统计的各省、自治区、直辖市的常住人口占全国人口比重的统计图.(注:图1中射线为两轴夹角的角平分线)
b.图2为七次人口普查中全国人口和年平均增长率的统计图,其中后两次统计中全国人口分为65岁以下人口和65岁及以上人口.
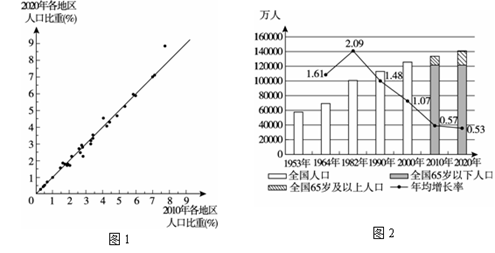
(说明:数据来自国家统计局官方网站,所有数据为大陆所有省、自治区、直辖市和现役军人的人口.)
根据以上信息,回答下列问题:
(1)从2010年到2020年,常住人口占全国人口的比重增长最多的是广东省,请在图1中用”○”圈出表示广东省的点;
(2)2010年各地区人口比重的方差为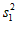 ,2020年各地区人口比重的方差为
,2020年各地区人口比重的方差为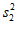 ,由图1可知
,由图1可知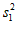
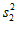 (填”>”,”<“,”=”).
(填”>”,”<“,”=”).
(3)由图2可知,下列推断合理的是
(填写序号).
①在这七次调查中,全国人口数量每次都在增加;
②在这七次调查中,从1982年往后,全国人口的年均增长率逐渐下降,说明全国人口每年增加的数量都在减小;
③当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化,从最近两次人口普查数据可以看出,中国老龄化问题日趋严重.
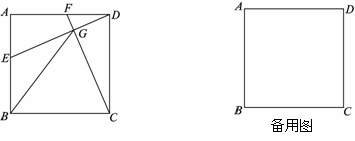
23.如图,在正方形ABCD中,E为AB边上一点(不与点A,B重合),CF⊥DE于点G,交AD于点F,连接BG.
(1)求证:AE=DF;
(2)是否存在点E的位置,使得△BCG为等腰三角形?若存在,写出一个满足条件的点E的位置并证明;若不存在,说明理由.
24.在数学课上,老师说统计学中常用的平均数不是只有算术平均数一种,好学的小聪通过网络搜索,又得到了两种平均数的定义,他把三种平均数的定义整理如下:
对于两个数a,b,
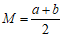 称为a,b这两个数的算术平均数,
称为a,b这两个数的算术平均数,
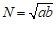 称为a,b这两个数的几何平均数,
称为a,b这两个数的几何平均数,
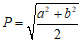 称为a,b这两个数的平方平均数.
称为a,b这两个数的平方平均数.
小聪根据上述定义,探究了一些问题,下面是他的探究过程,请你补充完整:
(1)若a = -1,b = -2,则M =
,N =
,P =
;
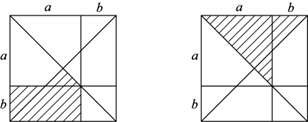
(2)小聪发现当a,b两数异号时,在实数范围内N没有意义,所以决定只研究当a,b都是正数时这三种平均数的大小关系.结合乘法公式和勾股定理的学习经验,他选择构造几何图形,用面积法解决问题:
如图,画出边长为a+b的正方形和它的两条对角线,则图1中阴影部分的面积可以表示N2.
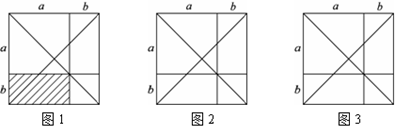
①请分别在图2,图3中用阴影标出一个面积为M2,P2的图形;
②借助图形可知当a,b都是正数时,M,N,P的大小关系是:
(把M,N,P从小到大排列,并用”<”或”≤”号连接).
25.对于两个实数a,b,规定Max(a,b)表示a,b两数中较大者,特殊地,当a = b时,Max(a,b)=a.如:Max(1,2)= 2,Max(-1,-2)= -1,Max(0,0)= 0.
(1)Max(-1,0)=
,Max(n,n -2)=
;
(2)对于一次函数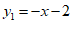 ,
,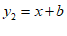 ,
,
①当x≥-1时,Max(y1,y2)= y2,求b的取值范围;
②当x=1-b时,Max(y1,y2)=p,当x=1+b时,Max(y1,y2)=q,若p≤q,直接写出b的取值范围.
【试题答案】
一、选择题(本题共24分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | C | C | B | D | D | A |
二、填空题(本题共24分,每小题3分)
题号 | 9 | 10 | 11 | 12 |
答案 | x ≥ 1 | 答案不唯一. 如:y =-x | 95 | 面试 |
题号 | 13 | 14 | 15 | 16 |
答案 | 6 | x>1 |
| ±1 |
三、解答题(本题共52分,17-22题,每小题5分,第23题7分,第24题7分,第25题8分)
17.解:原式=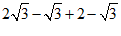 ……………………………………………4分
……………………………………………4分
=2. ……………………………………………………………………………5分
18.解:(1)补全图形如图所示.
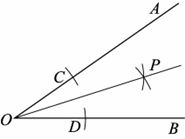
…………………………………………3分
(2)菱形;菱形的每一条对角线平分一组对角. ………………………………5分
19.证明:如图,连接AC交BD于点O. …………………1分
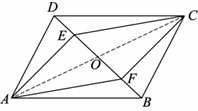
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD. …………………………3分
∵DE=BF,
∴OE=OF. …………………………………………………………………………4分
∴四边形AECF是平行四边形. ……………………………………………………5分
20.解:(1)设这个一次函数的表达式为y=kx+b.
∵一次函数的图象经过点(-1,0)和(0,2),
∴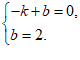
解得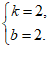
所以这个一次函数的表达式为y=2x+2.……………………………………3分
(2)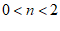 . …………………………………………………………5分
. …………………………………………………………5分
21.解:∵AC⊥l于点A,
∴∠CAH=90°.…………………………………………………………………1分
∴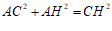 .……………………………………………………2分
.……………………………………………………2分
同理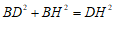 .
.
∵HC=HD,
∴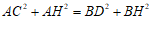 . …………………………………………3分
. …………………………………………3分
设AH=x,则BH=5-x.
∵AC=2,BD=3,
∴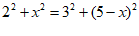 . ……………………………………………4分
. ……………………………………………4分
解得x=3. ……………………………………………………………………5分
即AH=3.
22.(1)如图所示.
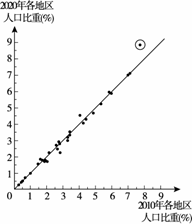
………………………………1分
(2)<.………………………………………………………………………………2分
(3)①③. ………………………………………………………………………5分
23.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°.……………………………………………………1分
∴∠ADE+∠AED=90°.
∵CF⊥DE于点G,
∴∠AED=∠DFC. ………………………………………………………………………2分
∴△AED≌△DFC.………………………………………………………………………3分
∴AE=DF.………………………………………………………………………………4分
(2)当点E为AB的中点时,△BCG为等腰三角形. ……………………………5分
证明:如图,延长CB交DE的延长线于点P.
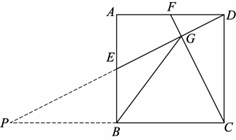
∵点E为AB的中点,
∴AE=BE.
∵∠A=∠ABP=90°,∠AED=∠BEP,
∴△AED≌△BEP.………………………6分
∴AD=BP=BC.
∵∠PGC=90°,
∴BG=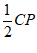 =BC. ……………………………………………………………………7分
=BC. ……………………………………………………………………7分
即△BCG为等腰三角形.
24.解:(1)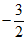 ,
,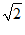 ,
,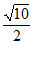 ;……………………………………………………3分
;……………………………………………………3分
(2)答案不唯一.如:
…………………………………5分
(3)N≤M≤P. ………………………………………………………………………7分
25.解:(1)0,n;…………………………………………………………………2分
(2)①可求直线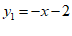 ,
,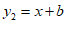 的交点坐标为
的交点坐标为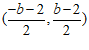 .……3分
.……3分
由题意可知当x≥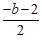 时,必有Max(y1,y2)= y2.……………………4分
时,必有Max(y1,y2)= y2.……………………4分
要想使x≥-1时,Max(y1,y2)= y2成立,
需满足-1≥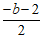 . ………………………………………………………5分
. ………………………………………………………5分
∴b≥0. ………………………………………………………………………6分
②b≥0或b≤- 4. …………………………………………………………8分
说明:各解答题的其他正确解法请参照以上标准给分.