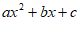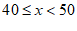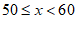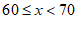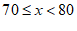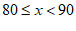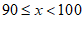北京市昌平区2020-2021学年下学期初中八年级期末质量抽测数学试卷
本试卷共100分。考试时长120分钟。
一、选择题(本题共16分,每小题2分)第1—8题均有四个选项,符合题意的选项只有一个。
1. 在平面直角坐标系中,点A(-2,3)在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中,下列云纹图案中,是中心对称图形的是
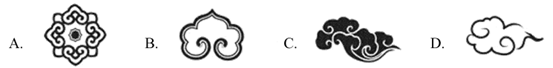
3. 如图,足球图片中的一块黑色皮块的内角和是

A. 180° B. 360° C. 540° D. 720°
4. 已知直线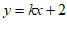 与直线
与直线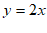 平行,则k的值是
平行,则k的值是
A. 2 B. -2 C. 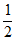 D.
D. 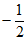
5. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 180 | 185 | 185 | 180 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
要选择一名成绩好且发挥稳定的运动员参加比赛,应该选择
A. 甲 B. 乙 C. 丙 D. 丁
6. 第七次全国人口普查结果发布:全国人口数超14.1亿,人口老龄化严重,2018年60岁及以上人口24949万人,2020年60岁及以上人口达到26402万人,设2018年到2020年60岁及以上人口的年平均增长率为x,则根据题意列出方程
A. 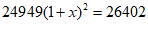 B.
B. 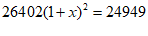
C. 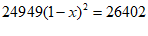 D.
D. 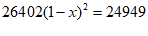
7. 如图,在四边形ABCD中,AB∥CD,下列条件不能判定此四边形为平行四边形的是
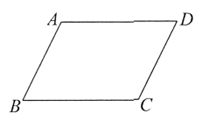
A. AB=CD B. AD∥BC C. ∠B=∠D D. AD=BC
8. 根据下列表格中的对应值判断方程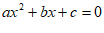 (
(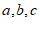 为常数,且
为常数,且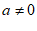 )的一个解x的取值范围
)的一个解x的取值范围
x | 3.23 | 3.24 | 3.25 | 3.26 |
| -0.06 | -0.02 | 0.03 | 0.09 |
A. 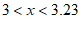 B.
B. 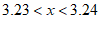
C. 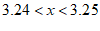 D.
D. 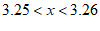
二、填空题(本题共16分,每小题2分)
9. 写出一个图象经过点(0,1)的函数的表达式_______________。
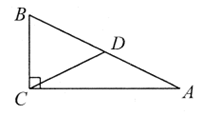
10. 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若∠A=26°,则∠BDC=______________°。
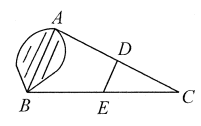
11. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为_________。
12. 直线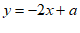 经过点
经过点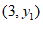 和
和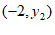 ,则
,则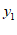 _________
_________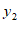 。(填”>”,”<”或”=”)
。(填”>”,”<”或”=”)
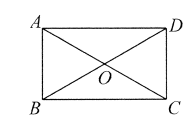
13. 如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOD=120°,BD=6,则AB的长为___________。
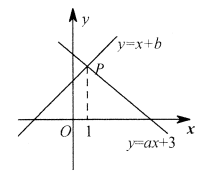
14. 如图,已知函数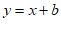 和
和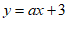 的图象交点为P,则关于x的不等式
的图象交点为P,则关于x的不等式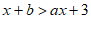 的解集为_______________。
的解集为_______________。
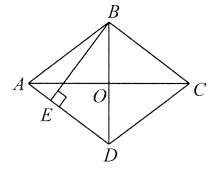
15. 如图,菱形ABCD的两条对角线AC,BD交于点O,BE⊥AD于点E,若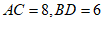 ,则BE的长为____________。
,则BE的长为____________。
16,
若一个函数图象经过点A(1,3),B(3,1),则关于此函数的说法:
①该函数可能是一次函数;
②点P(2,2.5),Q(2,3.5)不可能同时在该函数图象上;
③函数值y一定随自变量x的增大而减小;
④可能存在自变量x的某个取值范围,在这个范围内函数值y随自变量x增大而增大。
所有正确结论的序号是____________。
三、解答题(本题共12道小题,第17—22题,每小题5分,第23—26题,每小题6分,第27、28题,每小题7分,共68分)
17. 解方程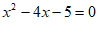 。
。
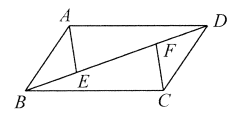
18. 如图,在平行四边形ABCD中,E,F是对角线BD上的两点,且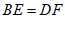 ,连接AE,CF。求证:AE=CF。
,连接AE,CF。求证:AE=CF。
19. 一次函数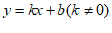 的图象经过点A(1,6)和点B(0,4)。
的图象经过点A(1,6)和点B(0,4)。
(1)求一次函数的表达式;
(2)若此一次函数图象与x轴交于点C,求△BOC的面积。
20. 关于x的一元二次方程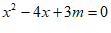 有实数根。
有实数根。
(1)求m的取值范围;
(2)写出一个符合条件的m的值,求出此时方程的根。
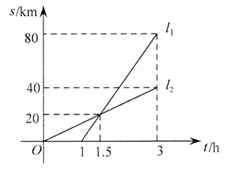
21. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地,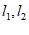 分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系。
分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系。
(1)乙出发_______h后,甲才出发;
(2)在乙出发__________h后,两人相遇,这时他们离开A地__________km;
(3)甲的速度是___________km/h,乙的速度是___________km/h。
22. 在平面直角坐标系中,四边形ABCD为矩形,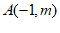 和
和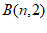 关于y轴对称。
关于y轴对称。
(1)m=____________,n=__________;
(2)矩形ABCD的中心在原点O,直线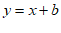 与矩形ABCD交于P,Q两点。
与矩形ABCD交于P,Q两点。
①当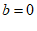 时,线段PQ长度为_____________;
时,线段PQ长度为_____________;
②当线段PQ长度最大时,求b的取值范围。
23. 下面是小静设计的作矩形ABCD的尺规作图过程。
已知:Rt△ABC中,∠ABC=90°。
求作:矩形ABCD。
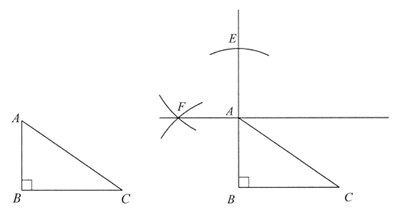
作法:如图,
①以点A为圆心,AB长为半径作弧,交BA的延长线于点E;
②分别以点B,E为圆心,大于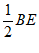 长为半径作弧,两弧交于点F,作直线AF;
长为半径作弧,两弧交于点F,作直线AF;
③以点C为圆心,BC长为半径作弧,交BC的延长线于点M;
④分别以点B,M为圆心,大于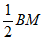 长为半径作弧,两弧交于点N,作直线CN;
长为半径作弧,两弧交于点N,作直线CN;
⑤直线AF与直线CN交于点D;
所以四边形ABCD是矩形。
(1)根据小静设计的尺规作图过程,使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明。
证明:
∵AB=_____________,BF=______________,
∴AF⊥BE,(__________________)(填推理的依据)
同理CN⊥BM。
又∵∠ABC=90°,
∴四边形ABCD是矩形,(________________________)(填推理的依据)
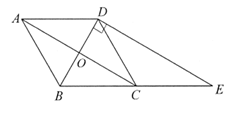
24. 已知:如图,在等腰△ABC中,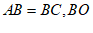 平分∠ABC交AC于点O,延长BO至点D,使
平分∠ABC交AC于点O,延长BO至点D,使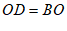 ,连接AD,CD,过点D作DE⊥BD交BC的延长线于点E。
,连接AD,CD,过点D作DE⊥BD交BC的延长线于点E。
(1)求证:四边形ABCD是菱形;
(2)如果AB=2,∠BAD=60°,求DE的长。
25. 2021年是中国共产党建党100周年,为了让学生了解更多的党史知识,某中学初二年级举行了一次”党史知识竞赛”,为了了解本次竞赛情况,从中抽取了初二年级50名学生,对他们此次竞赛的成绩(得分取正整数,满分为100分)整理并绘制了如下统计图表。
初二年级学生竞赛成绩的频数分布表
成绩分组/分 | 频数 | 频率 |
| 1 | 0.02 |
| a | 0.06 |
| 10 | 0.20 |
| b | c |
| 12 | 0.24 |
| 18 | 0.36 |
合计 | 50 | 1.00 |
初二年级学生竞赛成绩的频数分布直方图
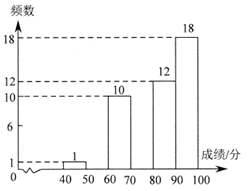
根据以上信息,回答下列问题:
(1)a=__________,b=__________,c=___________;
(2)补全频数分布直方图;
(3)已知该校初二年级有学生400人,估计该校初二年级学生竞赛成绩不低于80分的人数。
26. 如图,在平面直角坐标系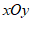 中,直线
中,直线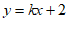 与直线
与直线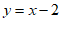 交于点
交于点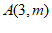 。
。
(1)求k、m的值;
(2)已知点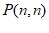 ,过点P作垂直于y轴的直线,交直线
,过点P作垂直于y轴的直线,交直线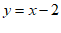 于点M,过点P作垂直于x轴的直线,交直线
于点M,过点P作垂直于x轴的直线,交直线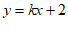 于点N。
于点N。
①当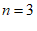 时,求△PMN的面积;
时,求△PMN的面积;
②若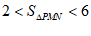 ,结合函数的图象,直接写出n的取值范围。
,结合函数的图象,直接写出n的取值范围。
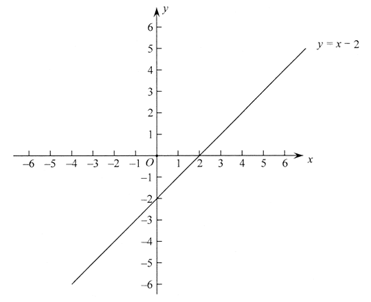
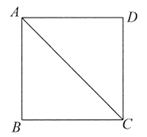
27. 如图,在正方形ABCD中,E是边AB上一动点(不与A、B重合),连接DE,交对角线AC于点F,过点F作DE的垂线分别交AD、BC于点M、N。
(1)根据题意,补全图形;
(2)证明:FD=FN;
(3)直接写出BN和AF的数量关系。
28. 在平面直角坐标系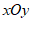 中的点
中的点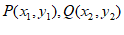 ,给出如下定义:
,给出如下定义:
若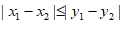 ,则
,则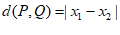 ;若
;若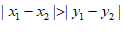 ,则
,则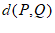 =
=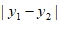 。
。
(1)已知点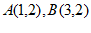 ,则
,则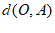 =___________,
=___________,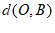 =_________;
=_________;
(2)点C坐标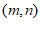 ,且
,且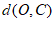 =1。
=1。
①当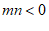 时,写出一个符合条件的点C的坐标__________;
时,写出一个符合条件的点C的坐标__________;
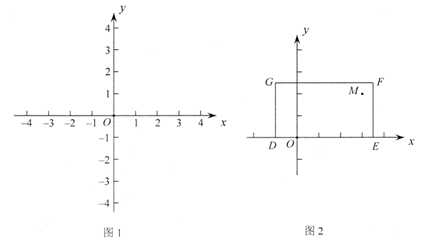
②所有符合条件的点C所组成的图形记作W,在图1中画出图形W;
(3)如图2,矩形DEFG中,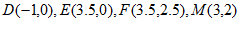 是矩形内部一点,N是矩形边上的点,且
是矩形内部一点,N是矩形边上的点,且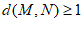 ,若直线
,若直线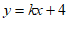 上存在点N,直接写出k的取值范围。
上存在点N,直接写出k的取值范围。
【试题答案】
一、选择题(本题共8道小题,每小题2分,共16分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | A | C | A | B | A | D | C |
二、填空题(本题共8道小题,每小题2分,共16分)
题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 |
(答案不唯一) | 52 | 20m | < | 3 |
|
| ①②④ |
三、解答题(本题共12道小题,第17—22题,每小题5分,第23—26题,每小题6分,第27、28题,每小题7分,共68分)
17. 解法1: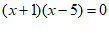 。 3分
。 3分
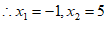 。 5分
。 5分
解法2: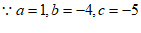 , 1分
, 1分
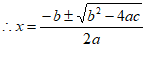 , 2分
, 2分
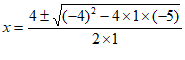
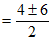 , 3分
, 3分
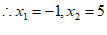 。 5分
。 5分
解法3: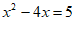 , 1分
, 1分
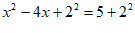 , 2分
, 2分
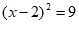 ,
,
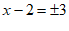 , 3分
, 3分
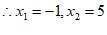 。 5分
。 5分
18. 证明:∵四边形ABCD为平行四边形,
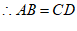 ,AB∥CD, 2分
,AB∥CD, 2分
∴∠ABD=∠CDB, 3分
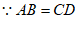 ,∠ABD=∠CDB,
,∠ABD=∠CDB,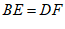
∴△ABE≌△CDF, 4分
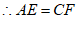 。 5分
。 5分
19. 解:(1)∵一次函数的图象经过点A(1,6)和点B(0,4),
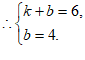
解得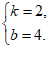 2分
2分
∴这个一次函数的表达式为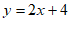 。 3分
。 3分
(2)∵直线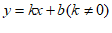 与x轴交于点C,
与x轴交于点C,
∴令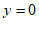 ,则
,则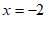 ,
,
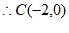 , 4分
, 4分
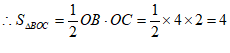 。 5分
。 5分
20. 解:(1)∵一元二次方程有实数根,
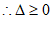 , 1分
, 1分
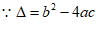
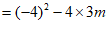
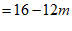 , 2分
, 2分
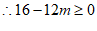
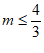 。 3分
。 3分
(2)当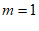 时,方程为
时,方程为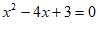 ,
,
解得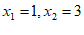 。(答案不唯一) 5分
。(答案不唯一) 5分
21. 解:(1)1; 1分
(2)1.5,20; 3分
(3)40;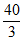 。 5分
。 5分
22. (1)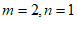 ; 2分
; 2分
(2)①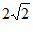 ; 3分
; 3分
②把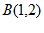 代入
代入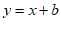 ,得
,得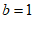 ;
;
把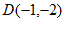 代入
代入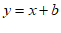 ,得
,得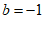 ; 4分
; 4分
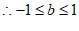 。 5分
。 5分
23. 解:(1)正确补全图形;
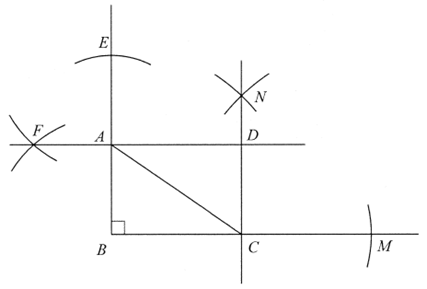
2分
(2)AE 3分
EF 4分
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。 5分
有三个角是直角的四边形是矩形。 6分
24. (1)证明: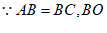 平分∠ABC,
平分∠ABC,
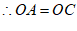 , 1分
, 1分
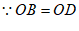 ,
,
∴四边形ABCD为平行四边形, 2分
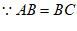 ,
,
∴四边形ABCD是菱形。 3分
(2)解:∵四边形ABCD是菱形,
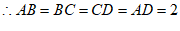 ,AD∥BC,AC⊥BD,
,AD∥BC,AC⊥BD,
∵∠BAD=60°,
∴△ABD为等边三角形,
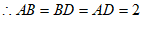 , 4分
, 4分
∵DE⊥BD,AC⊥BD,
∴AC∥DE,
∵AD∥CE,AC∥DE,
∴四边形ACED是平行四边形,
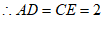 ,
,
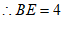 , 5分
, 5分
∵DE⊥BD,
∴△BDE为直角三角形。
∵在Rt△BDE中,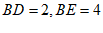 ,
,
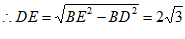 。 6分
。 6分
25. 解:(1)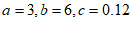 ; 3分
; 3分
(2)正确补全图形 5分
初二年级学生竞赛成绩的频数分布直方图
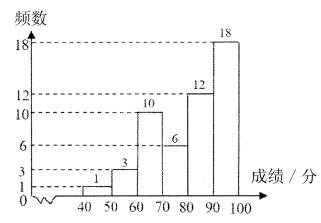
(3)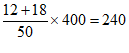 (人) 6分
(人) 6分
答:该校初二年级学生竞赛成绩不低于80分的有240人。
26. (1)将点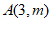 代入
代入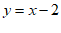 ,得
,得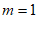 。 1分
。 1分
∴点A的坐标为(3,1),
将点A(3,1)代入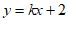 ,得
,得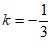 。 2分
。 2分
(2)①当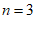 时,如图
时,如图
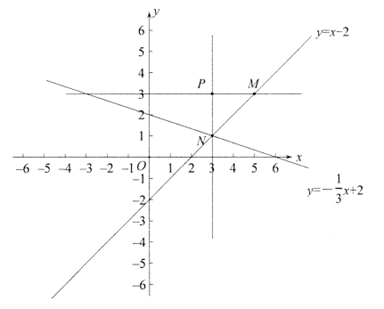
∵点P的坐标为(3,3)且PM平行于x轴,PN平行于y轴,
∴设M的坐标为(a,3),N的坐标为(3,b),
将点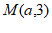 代入
代入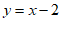 ,得
,得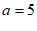 ,
,
将点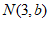 代入
代入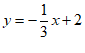 ,得
,得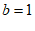 ,
,
∴M的坐标为(5,3),N的坐标为(3,1),
∵点P的坐标为(3,3),
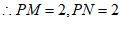 ,
,
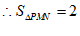 , 4分
, 4分
②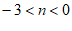 或
或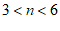 。 6分
。 6分
27. (1)依题意,补全图形。 2分
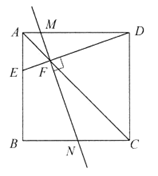
(2)证明:过点F作FG⊥CD交CD于点G,过点F作FH⊥BC交BC于点H,
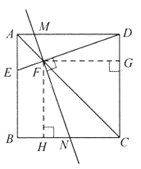
∵四边形ABCD是正方形,AC为正方形一条对角线,
∴∠BCD=90°,∠BCA=∠DCA=45°,
∵FG⊥CD,FH⊥BC,
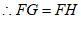 , 3分
, 3分
∠FGC=∠FHC=90°,
∴四边形FHCG是正方形,
∴∠HFG=90°,
∵MN⊥DE,
∴∠NFD=90°,
∴∠NFD-∠NFG=∠HFG-∠NFG,
∴∠DFG=∠NFH。 4分
在△DFG和△NFH中
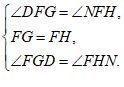
∴△DFG≌△NFH,
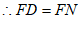 。 5分
。 5分
(3)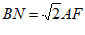 。 7分
。 7分
28. (1)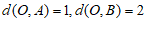 ; 2分
; 2分
(2)①点C的坐标为(-1,1);(答案不唯一) 3分
②如图1
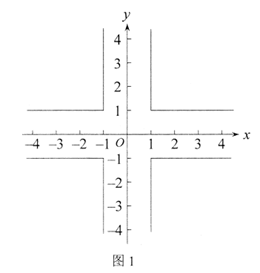
5分
(3)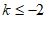 或
或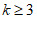 。 7分
。 7分