北京市怀柔区2020-2021学年下学期初中七年级期末考试数学试卷
一、选择题
1. (-a5)2+(-a2)5的结果是( )
A. 0 B. 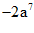 C.
C. 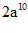 D.
D. 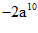
2. 如图:点C是直线AB上一点,过点C作CD⊥CE,那么图中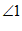 和
和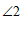 的关系是( ).
的关系是( ).
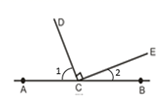
A. 互补 B. 互余 C. 对顶角 D. 同位角
3. 不等式2x-3>1的解集在数轴上表示正确的是( )
A
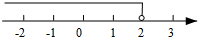 B.
B. 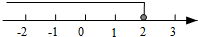
C. 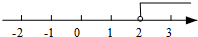 D.
D. 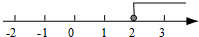
4. 已知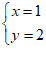 是方程
是方程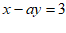 的一个解,那么a的值为( )
的一个解,那么a的值为( )
A. 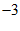 B.
B. 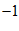 C. 1 D. 3
C. 1 D. 3
5. 如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=35°,那么∠B的度数为( )
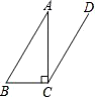
A. 35° B. 45° C. 55° D. 145°
6. 某健步走运动爱好者用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,众数和中位数分别是( )
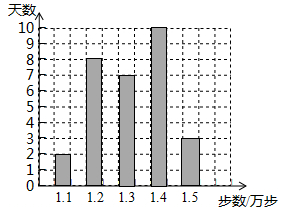
A. 1.2,1.3 B. 1.3,1.3
C. 1.4,1.35 D. 1.4,1.3
7. 鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:”今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
8. 将 3a2m-6amn+3a分解因式,下面是四位同学分解的结果:①3am(a-2n+1);②3a(am+2mn-1);③3a(am-2mn);④3a(am-2mn+1).其中,正确的是( )
A. ① B. ② C. ③ D. ④
9. 某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(度) | 电费价格(元/度) |
| 0.48 |
| 0 |
| 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A. 100 B. 400 C. 396 D. 397
10. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个”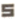 “的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
“的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
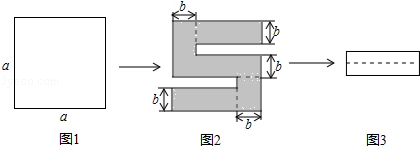
A. 2a-3b B. 4a-8b C. 2a-4b D. 4a-10b
二、填空题
11. 分解因式:3a2-6a+3=____.
12. 若a+b=5, ab=6,则a2+b2=________
13. 图是根据某校为地震灾区捐款的情况而制作的统计图,已知该校在校学生有600人,请根据统计图计算该校共捐款_______元.

14. 已知,如图,要使得AB∥CD,你认为应该添加的一个条件是________
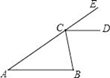
15. 写出不等式组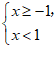 的整数解为__________.
的整数解为__________.
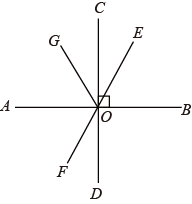
16. 如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,如果∠FOD = 28°,那么∠AOG =______度.
17. 已知x,y是有理数,且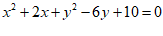 ,则
,则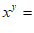 _________.
_________.
18. 将边长为1的正方形纸片按如图所示方法进行对折,第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,则S4=_____,S1+S2+S3+…+S2021=______.

三、解答题
19. 计算:
(1)(π-2021)0-(-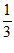 )-2+(-3)2
)-2+(-3)2
(2)(2x2)3•(-4y3)÷(4xy)2
20. 解不等式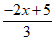 +1≤3,并把解集在数轴上表示出来.
+1≤3,并把解集在数轴上表示出来.
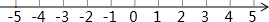
21. 因式分解:(1) ;(2)
;(2)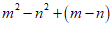

22. 解方程组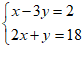 .
.
23. 已知: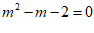 ,求代数式
,求代数式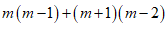 的值.
的值.
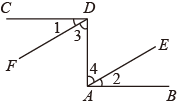
24. 如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).
25. 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
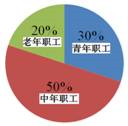
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
(1)扇形统计图中老年职工所占部分的圆心角度数为
(2)小张、小王和小李三人中, 的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
26. 已知关于x,y的方程组 的x,y的值之和等于2,求m的值.
的x,y的值之和等于2,求m的值.
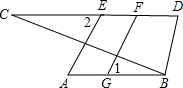
27. 如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
28. 为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b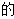 值;
值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
29. 探究题:学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题.
(1)小明遇到了下面的问题:如图1,l1∥l2,点P在l1、l2内部,探究∠A,∠APB,∠B的关系.小明过点P作l1的平行线,可证∠APB,∠A,∠B之间的数量关系是:∠APB=
.
(2)如图2,若AC∥BD,点P在AC、BD外部,∠A,∠B,∠APB的数量关系是否发生变化?请你补全下面的证明过程.
过点P作PE∥AC.
∴∠A=
∵AC∥BD
∴
∥
∴∠B=
∵∠BPA=∠BPE-∠EPA
∴
.
(3)随着以后的学习你还会发现平行线的许多用途,试构造平行线解决以下问题:已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°.
【试题答案】
一、选择题
1. A
【解析】
【分析】直接利用幂的乘方运算法则化简进而合并求出答案.
【详解】(-a5)2+(-a2)5=a10-a10=0.
故选A.
【点睛】此题主要考查了幂的乘方运算,正确化简各式是解题关键.
2. B
【解析】
【分析】根据角的和差、余角的性质计算,即可得到答案.
【详解】∵CD⊥CE
∴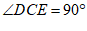
∵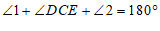
∴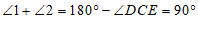
∴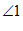 和
和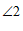 互余
互余
故选:B.
【点睛】本题考查了角的知识;解题的关键是熟练掌握角的和差、余角、垂线的性质,从而完成求解.
3. C
【解析】
【分析】由题意先求出不等式的解,然后再在数轴上表示即可排除选项.
【详解】解:由不等式2x-3>1可得: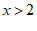 ,
,
在数轴上表示如图所示:
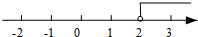
故选C.
【点睛】本题主要考查一元一次不等式的解法,熟练掌握一元一次不等式的解法是解题的关键.
4. B
【解析】
【分析】根据方程的解满足方程,可得关于a的方程,根据解方程,可得答案.
【详解】解:由题意,得
1-2a=3,
解得a=-1,
故答案为B.
【点睛】本题考查了二元一次方程的解的概念,利用方程的解满足方程得出关于a的方程是解题关键.
5. C
【解析】
 详解】∵CD∥AB,
详解】∵CD∥AB,
∴∠A=∠ACD=35°,
∴∠B=90°
−35°=55°,
故选C.
6. D
【解析】
【分析】中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),众数是一组数据中出现次数最多的数据,据此判断即可.
【详解】解:∵这组数据中1.4出现的次数最多,
∴在每天所走的步数这组数据中,众数是1.4;
每天所走的步数的中位数是:
(1.3+1.3)÷2=1.3,
∴在每天所走的步数这组数据中,众数和中位数分别是1.4、1.3.
故选:D.
【点睛】本题主要考查了众数、中位数的含义和求法,要熟练掌握,解答此题的关键是要明确:将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,众数是一组数据中出现次数最多的数据.
7. D
【解析】
【分析】设笼中有x只鸡,y只兔,根据上有35个头、下有94只脚,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【详解】设笼中有x只鸡,y只兔,根据题意得:
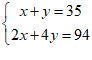
解得: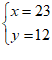 .
.
故选D.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
8. D
【解析】
【分析】由提公因式法可直接进行排除选项.
【详解】解: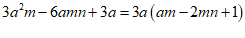 ;
;
∴只有④是正确的;
故选D.
【点睛】本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.
9. C
【解析】
【分析】先判断出电费是否超过400度,然后根据不等关系:七月份电费支出不超过200元,列不等式计算即可.
【详解】解:0.48×200+0.53×200
=96+106
=202(元),
故七月份电费支出不超过200元时电费不超过400度,
依题意有0.48×200+0.53(x-200)≤200,
解得x≤396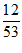 .
.
答:李叔家七月份最多可用电的度数是396.
故选C.
【点睛】本题考查了列一元一次不等式解实际问题 运用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的不等关系.
运用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的不等关系.
10.B
【解析】
【详解】试题分析:根据题意得:2(a-b+a-3b)=2(2a-4b)=4a-8b,
故选B
考点:1、列代数式;2、整式的计算
二、填空题
11. 3(a-1)2.
【解析】
【详解】解:原式=3(a2-2a+1)=3(a-1)2.
故答案为:3(a-1)2.
【点睛】本题考查提公因式法与公式法的综合运用.
12. 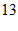 .
.
【解析】
【分析】利用完全平方公式理清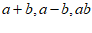 三式之间的关即可求解.
三式之间的关即可求解.
【详解】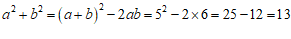
考点:完全平方式.
13. 7554
【解析】
【分析】由题意易得该校各年级的人数,然后再结合条形统计图可得总捐款数.
【详解】解:由统计图可得:
初一的人数为600×32%=192(名);初二的人数为600×33%=198(名);初三的人数为600×35%=210(名);
∴该校共捐款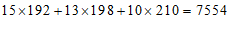 (元);
(元);
故答案为7554.
【点睛】本题主要考查扇形统计图及条形统计图,熟练掌握扇形统计图及条形统计图是解题的关键.
14.∠ECD=∠A(答案不唯一).
【解析】
【分析】根据平行线的判定定理,即可直接写出条件.
【详解】添加的条件是:∠ECD=∠A(答案不唯一).
故答案为∠ECD=∠A.
【点睛】本题考查了平行线的判定定理,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生”执果索因”的思维方式与能力.
15.-1和0.
【解析】
【分析】先根据”大小小大中间找”确定出不等式组的解集,继而可得不等式组的整数解.
【详解】解:∵不等式组的解集为-1≤x<1,
∴不等式组的整数解为-1、0,
故答案为-1、0.
【点睛】本题考查的是一元一次不等式组的整数解,熟知”同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
16. 59
【解析】
【详解】∵AB⊥CD,
∴∠AOD=90°,
∵∠FOD=28°,
∴∠AOF=90°−28°=62°,
∴∠AOE=180°-62°=118°,
∵OG平分∠AOE,
∴∠AOG=118°÷2=59°,
故答案为59°.
17.-1
【解析】
【详解】∵x2+y2+2x−6y+10=0,
∴x2+2x+1+y2−6y+9=0,
即(x+1)2+(y−3)2=0,
∴x+1=0,y−3=0,
∴x=−1,y=3,
∴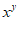 =-1.
=-1.
故答案为-1 .
18.①. 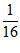 ②.
②. 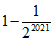
【解析】
【分析】根据翻折变换表示出所得图形的面积,再根据句各部分图形的面积之和等于正方形面积减去剩下部分的面积进行计算即可得解.
【详解】解:由题意得:
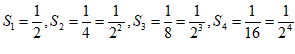 ……;
……;
∴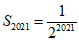 ,
,
∴S1+S2+S3+…+S2021=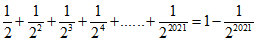 ;
;
故答案为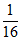 ,
,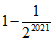 .
.
【点睛】本题主要考查图形规律及有理数的运算,关键在于观察各部分图形的面积之和等于正方形面积减去剩下部分的面积.
三、解答题
19. 计算:
(1)1;(2)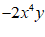
【解析】
【分析】(1)根据零次幂、负指数幂可直接进行求解;
(2)根据积的乘方及单项式乘除运算即可求解.
【详解】解:(1)原式=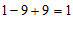 ;
;
(2)原式=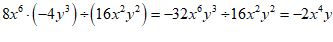 .
.
【点睛】本题主要考查零次幂、负指数幂及整式的乘除法运算,熟练掌握零次幂、负指数幂及整式的乘除法运算是解题的关键.
20. 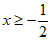 ,在数轴上表示见解析
,在数轴上表示见解析
【解析】
【分析】先对不等式进行求解,然后再在数轴上表示即可.
【详解】解: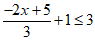
去分母得: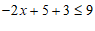 ,
,
移项合并同类项得: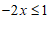 ,
,
解得: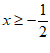 ;
;
在数轴上的表示如图所示:

【点睛】本题主要考查一元一次不等式的解法,熟练掌握一元一次不等式的解法是解题的关键.
21.(1)(x-3) 2 ;(2)(m-n) (m+n+1) .
【解析】
【详解】分析:
(1)根据本题特点,直接用”完全平方公式”分解即可;
(2)根据本题特点,先将前两项用”平方差公式”分解,再用”提公因式法”分解即可.
详解:
(1)原式= (x-3) 2 .
(2)原式= (m+n) (m-n)+ (m-n)= (m-n) (m+n+1) .
点睛:熟记”完全平方公式: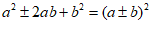 及平方差公式:
及平方差公式: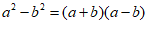 “是解答本题的关键.
“是解答本题的关键.
22. 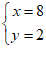
【解析】
 分析】根据加减消元进行求解方程组即可.
分析】根据加减消元进行求解方程组即可.
【详解】解: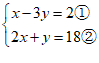
①+②×3得: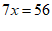 ,
,
解得: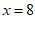 ,
,
把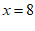 代入①得:
代入①得: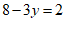 ,
,
解得: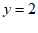 ,
,
∴原方程组的解为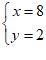 .
.
【点睛】本题主要考查二元一次方程组的解法,熟练掌握二元一次方程组的解法是解题的关键.
23.原式=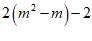 = 2
= 2
【解析】
【详解】试题分析:由m2-m-2=0可变化为m2-m=2,将m(m-1)+(m+1)(m-2)转化为2(m2-m)-2,再将m2-m作为一个整体代入,即可求出该式的值.
试题解析:原式=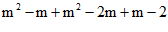 =
=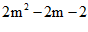 =
=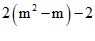
∵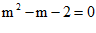
∴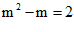
∴原式= 2×2-2 = 2
24. CD⊥DA,DA⊥AB,垂直定义,∠3=∠4,等角的余角相等,内错角相等,两直线平行.
【解析】
【分析】先根据垂直的定义,得到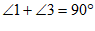 ,
,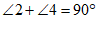 ,再根据等角的余角相等,得出
,再根据等角的余角相等,得出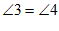 ,最后根据内错角相等,两直线平行进行判定即可.
,最后根据内错角相等,两直线平行进行判定即可.
【详解】证明:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°,(垂直定义)
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴∠3=∠4,(等角的余角相等)
∴DF∥AE.(内错角相等,两直线平行)
【点睛】本题主要考查了平行线的判定以及垂直的定义,解题时注意:内错角相等,两直线平行.
25.(1)72°;(2)小李.
【解析】
【分析】(1)用360°乘以老年职工所占部分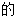 百分比可得;
百分比可得;
(2)根据各个样本的抽取中是否有代表性、随机性和广泛性确定答案即可.
【详解】(1)扇形统计图中老年职工所占部分的圆心角度数为360°×20%=72°,
故答案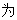 72°;
72°;
(2)小李的抽样调查的数据能够较好地反映出该单位职工健康情况,
小张的抽样调查的数据只有3个,样本容量太少.小王的抽样调查的数据主要集中在中青年职工,样本不够全面.
故答案为小李.
【点睛】此题主要考查了抽样调查的可靠性以及扇形统计图,正确理解抽样调查的随机性是解题关键.
26. m的值是4.
【解析】
【分析】把原方程组消去m后,与x+y=2建立新的方程组,求得x,y的值后,再代入原方程组中,求得m的值.
【详解】关于x,y的方程组为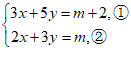
由①-②得x+2y=2,
∵x,y的值之和等于2,
∴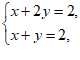 解这个方程组得
解这个方程组得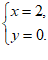
把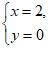 代入②得m=4.
代入②得m=4.
∴m的值是4.
【点睛】本题的实质是解三元一次方程组,用加减法或代入法来解答.
27.见解析
【解析】
【分析】首先由AE⊥BC,FG⊥BC可得AE∥FG,根据两直线平行,同位角相等及等量代换可推出∠A=∠2,利用内错角相等,两直线平行可得AB∥CD.
【详解】证明:如图,设BC与AE、GF分别交于点M、N.
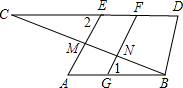
∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNB=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
【点睛】本题考查了平行线的性质及判定,熟记定理是正确解题的关键.
28.(1)购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.
(2)购车总费用最少的是购买A型公交车8辆,购买B型公交车2辆.
【解析】
【详解】解:(1)由题意得: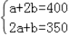 ,解这个方程组得:
,解这个方程组得: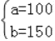 .
.
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.
(2)设购买A型公交车x辆,购买B型公交车(10-x)辆,
由题意得: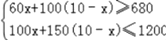 ,解得:6≤x≤8,
,解得:6≤x≤8,
有三种购车方案:①购买A型公交车6辆,购买B型公交车4辆;
②购买A型公交车7辆,购买B型公交车3辆;
③购买A型公交车8辆,购买B型公交车2辆.
故购买A型公交车越多越省钱,
所以购车总费用最少的是购买A型公交车8辆,购买B型公交车2辆.
29.(1)∠A+∠B;(2)∠APE,PE,BD,∠BPE,∠APB=∠B-∠A;(3)见详解.
【解析】
【分析】(1)设过点P作l1的平行线为PF,由题意易得∠B=∠FPB,∠A=∠FPA,然后问题可求解;
(2)由题意结合平行线的性质可直接进行求解;
(3)过点A作DE∥BC,则有∠B=∠BAD,∠C=∠CAE,然后根据平角的意义可求证.
【详解】解:(1)设过点P作l1的平行线为PF,如图所示:
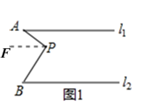
∵l1∥l2,
∴l1∥l2∥PF,
∴∠B=∠FPB,∠A=∠FPA,
∵∠APB=∠FPB+∠FPA,
∴∠APB=∠A+∠B;
故答案为∠A+∠B;
(2)过点P作PE∥AC,
∴∠A=∠APE
∵AC∥BD
∴PE∥BD
∴∠B=∠BPE
∵∠BPA=∠BPE-∠EPA
∴∠APB=∠B-∠A;
故答案为∠APE,PE,BD,∠BPE,∠APB=∠B-∠A;
(3)过点A作DE∥BC,如图所示:
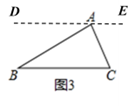
∴∠B=∠BAD,∠C=∠CAE,
∵∠BAC+∠BAD+∠CAE=180°,
∴∠BAC+∠B+∠C=180°.
【点睛】本题主要考查平行线的性质与判定及平角的意义,熟练掌握平行线的性质与判定及平角的意义是解题的关键.

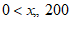
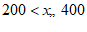
 53
53