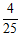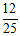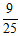本试卷满分共150分
考试时间120分钟
第一部分(选择题
共40分)
一、选择题:共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项。
(1)在复平面内,复数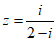 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
(2)下列函数中,在区间(0,+∞)上单调递增的是
(A) 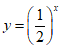 (B)
(B) 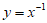 (C)
(C) 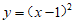 (D)
(D)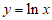
(3)已知向量a=(-1,2),b=(2,m),若a∥b,则m=
(A) -4 (B) 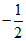 (C)
(C) 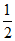 (D)4
(D)4
(4)在平面直角坐标系xOy中,角α以Ox为始边,它的终边与以原点O为圆心的单位圆的交点为P(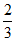 ,y0),则
,y0),则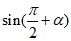 =
=
(A) 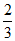 (B)
(B) 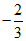 (C)
(C) 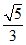 (D)
(D)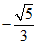
(5)已知α,β,γ是三个不同的平面,a,b是两条不同的直线,下列命题中正确的是
(A)若α⊥γ,β⊥γ,则α∥β
(B)若a⊥α,b⊥α,则a∥b
(C)若a∥α,b∥α,则a∥b
(D)若a∥α,a∥β,则α∥β
(6)”a=1″是“直线x+ay-1=0与直线ax-y+1=0相互垂直“的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(7)已知双曲线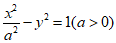 的渐近线与圆
的渐近线与圆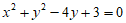 相切,则a=
相切,则a=
(A)3 (B) 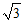 (C)
(C) 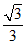 (D)
(D)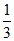
(8)将函数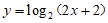 的图象向下平移1个单位长度,再向右平移1个单位长度,得到函数g(x)的图象,则g(x)=
的图象向下平移1个单位长度,再向右平移1个单位长度,得到函数g(x)的图象,则g(x)=
(A) log2 (2x+1)-1 (B) log2 (2x+1)+1
(C)log2x-1 (D) log2x
(9)某中学举行“十八而志,青春万岁“成人礼,现在需要从4个语言类节目和6个歌唱类节目中各选2个节目进行展演,则语言类节目A和歌唱类节目B至少有一个被选中的不同选法种数是
(A)15 (B)45 (C)60 (D)75
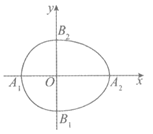
(10)如图,半椭圆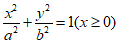 与半椭圆
与半椭圆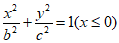 组成的曲线称为“果圆“,其中a2=b2+c2,a>0,b>c>0.A1,A2和B1,B2分别是“果圆“与x轴,y轴的交点.给出下列三个结论:
组成的曲线称为“果圆“,其中a2=b2+c2,a>0,b>c>0.A1,A2和B1,B2分别是“果圆“与x轴,y轴的交点.给出下列三个结论:
①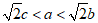 ;
;
②若|A1A2|=|B1B2|,则 a: b: c =5:4: 3;
③若在“果圆“y轴右侧部分上存在点P,使得∠A1PA2=90°,则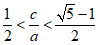 .
.
其中,所有正确结论的序号是
(A)①② (B)①③ (C)②③ D)①②③
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分.
(11)函数f(x)=sinx+cosx的值域为______________.
(12)能够说明“若a,b,m均为正数,则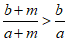 “是假命题的一组整数a,b的值依次为________________.
“是假命题的一组整数a,b的值依次为________________.
(13)已知点P(x0,y0)为抛物线C:x2=4y上的点,且点P到抛物线C焦点的距离为3,则|x0|=_____________.
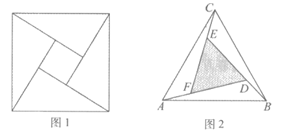
(14)赵爽是我国古代数学家,大约在公元222年,他为《周髀算经》一书作序时,介绍了“赵爽弦图“——由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图1所示,类比“赵爽弦图“,可构造如图2所示的图形,它是由3个全等的三角形与中间一个小等边三角形拼成的一个大等边三角形.在△ABC中,若AF=1,FD =2.则AB=______________.
(15)函数f(x)是定义域为R的奇函数,满足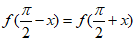 ,且当x∈[0,π)时,
,且当x∈[0,π)时,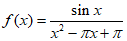 ,给出下列四个结论:
,给出下列四个结论:
①f(π) =0;
②π是函数f(x)的周期;
③函数f(x)在区间(-1,1)上单调递增;
④函数g(x) =f(x) -sin1(x∈[-10,10])所有零点之和为3π.
其中,正确结论的序号是____________.
三、解答题共6小题,共85分,解答应写出文字说明,演算步骤或证明过程.
(16)(本小题13分)
已知数列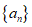 中,a1=1,且满足____________.
中,a1=1,且满足____________.
(I)求数列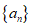 的通项公式;
的通项公式;
(Ⅱ)求数列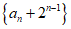 的前n项和Sn.
的前n项和Sn.
从①an+1=2an(n∈N*);②an+1-an=2(n∈N*);③an+1+an=2(n∈N*)这三个条件中选择一个,补充在上面的问题中并作答.
注:如果选择多个条件分别解答,按第一个解答计分.
(17)(本小题14分)
某公司开发了一款手机应用软件,为了解用户对这款软件的满意度,推出该软件3个月后,从使用该软件的用户中随机抽查了1000名,将所得的满意度的分数分成7组:[30,40),[40,50),…,[90,100],整理得到如下频率分布直方图.
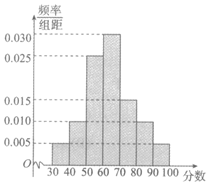
根据所得的满意度的分数,将用户的满意度分为两个等级:
满意度的分数 | [30,60) | [60,100] |
满意度的等级 | 不满意 | 满意 |
(I)从使用该软件的用户中随机抽取1人,估计其满意度的等级为“满意“的概率;
(Ⅱ)用频率估计概率,从使用该软件的所有用户中随机抽取2人,以X表示这2人中满意度的等级为“满意“的人数,求X的分布列和数学期望.
(18)(本小题14分)
如图,在多面体ABCDEF中,四边形ABCD和CDEF都是直角梯形,AB∥CD,CD∥EF,AB=EF=1,DA=DC=DE=2,∠ADE=∠ADC=∠EDC=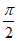 ,点M为棱CF上一点,平面AEM与棱BC交于点N.
,点M为棱CF上一点,平面AEM与棱BC交于点N.
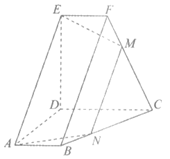
(I)求证:ED⊥平面ABCD;
(Ⅱ)求证:AE∥MN;
(Ⅲ)若平面AEM与平面CDEF所成锐二面角的余弦值为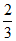 ,求
,求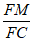 的值.
的值.
(19)(本小题15分)
已知函数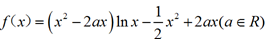 .
.
(I)若a=0,求f(x)的最小值;
(Ⅱ)求函数f(x)的单调区间.
(20)(本小题15分)
已知椭圆C: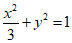 ,过点(-1,0)的直线l交椭圆C于点A,B.
,过点(-1,0)的直线l交椭圆C于点A,B.
(I)当直线l与x轴垂直时,求|AB|;
(Ⅱ)在x轴上是否存在定点P,使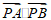 为定值?若存在,求点P的坐标及
为定值?若存在,求点P的坐标及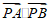 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(21)(本小题14分)
设数集S满足:①任意x∈S,有x≥0;②任意x,y∈S,有x+y∈S或|x-y|∈S,则称数集S具有性质P.
(I)判断数集A={0,1,2,4}是否具有性质P,并说明理由;
(Ⅱ)若数集B={a1,a2,…,an}且ai<ai+1(i=1,2,…,n-1)具有性质P.
(i)当n=2021时,求证:a1,a2,…,an是等差数列;
(ii)当a1,a2,…,an不是等差数列时,写出n的最大值.(结论不需要证明)
参考答案
一、选择题(共10小题,每小题4分,共40分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | D | A | A | B | A | C | D | C | D |
二、填空题(共5小题,每小题5分,共25分)
11.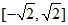 12.1,2(答案不唯一) 13.
12.1,2(答案不唯一) 13.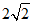
14.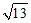 15.①③④
15.①③④
三、解答题(共6小题,共85分)
16.(本小题13分)
解:选①
(I)因为an+1= 2an(n∈N*),
所以数列{an}是以1为首项,2为公比的等比数列, ……2分
所以an=1×2n-1= 2n-1……… 4分
数列{an}的通项公式为an=2n-1(n∈N*). ……6分
(II)an+2n-1=2n-1+2n-1=2n ……………………8分
所以数列{an+2n-1)是以2为首项,2为公比的等比数列.……………………10分
所以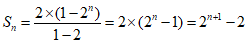 …………………………13分
…………………………13分
选②
(I)因为an+1-an=2(n∈N*),
所以数列{an}是以1为首项,2为公差的等差数列. ……………………2分
所以an=1+(n-1)×2=2n-1.………………………………………………4分
数列{an}的通项公式为an=2n-1(n∈N*). ………………………………6分
(II)an+2n-1=2n-1+2n-1, …………………………………………8分
所以Sn= (1+3+…+2n-1)+(1+2+…+2n-1)
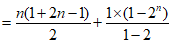
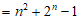 …………………………………13分
…………………………………13分
选③
(I)因为an+1+an=2(n∈N*),
所以an+an-1=2,(n≥2,n∈N*). …………………………2分
两式相减得an+1-an-1=0,(n≥2,n∈N*), ………………………………4分
即an+1=an-1(n≥2,n∈N*). …………………………6分
又因为a1=a2=1,
所以数列{an}是常数列,………………………………………………7分
故数列{an}的通项公式为an=1(n∈N*). ………………………………8分
(II)an+2n-1 =1+2n-1,
所以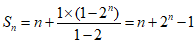 ……………13分
……………13分
17.(本小题14分)
解:(I)根据频率分布直方图可知,样本中[60,100]的频率为:
(0.030+0.015+0.010+0.005) ×10=0.6, …………………………………3分
所以从使用该软件的用户中随机抽取1人,其满意度的等级为“满意“的概率约为0.6.
……………………………………4分
(II)用频率估计概率,则“满意“的概率为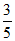 ,“不满意“的概率为
,“不满意“的概率为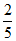 .…………5分
.…………5分
X的所有可能取值为0,1,2. ………………………6分
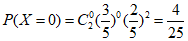 ; …………………8分
; …………………8分
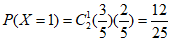 ;……………………………………10分
;……………………………………10分
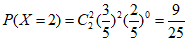 ;………………………………12分
;………………………………12分
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
数学期望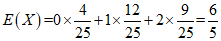 ………………………………14分
………………………………14分
(18)(本小题14分)
(I)证明:因为∠ADE=∠EDC= 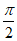 ,
,
所以ED⊥AD,ED⊥DC. …………………2分
因为AD 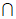 DC=D,AD,DC
DC=D,AD,DC 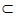 平面ABCD, …………3分
平面ABCD, …………3分
所以ED⊥平面ABCD. ……………………………4分
(II)证明:因为AB∥CD,CD∥EF,
所以AB∥EF. ……………………………………………5分
因为AB=EF,
所以四边形ABFE是平行四边形. ……………………………………6分
所以AE∥BF.
因为AE 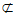 平面BCF,BF
平面BCF,BF  平面BCF,
平面BCF,
所以AE∥平面BCF. ……………………………………7分
因为AE 平面AEM,平面AEM
平面AEM,平面AEM  平面BCF=MN,
平面BCF=MN,
所以AE∥MN. ………………………………………8分
(III)解:因为ED⊥AD,ED⊥DC,AD⊥DC,所以如图建立空间直角坐标系D-xyz,
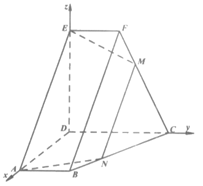
由AB=EF=1,DA=DC=DE=2,可知D(0,0,0),A(2,0,0), B(2,1,0),C(0,2,0),E(0,0,2),F(0,1,2),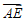 =(-2,0,2),
=(-2,0,2),
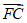 =(0,1,-2), ……9分
=(0,1,-2), ……9分
设
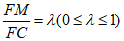 ,
,
则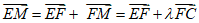
=(0,1,0)+λ(0,1,-2)=(0,1+λ,-2λ),
设m=(x,y,z)是平面AEM的法向量,
则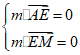 ,即
,即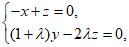 ,…………10分
,…………10分
所以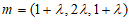 . …………11分
. …………11分
因为n =(1,0,0)是平面CDEF的法向量,
所以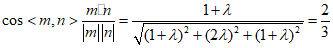 ………………12分
………………12分
因为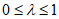 ,解得
,解得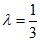 . …………13分
. …………13分
所以平面AEM与平面CDEF所成锐二面角的余弦值为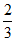 时,
时,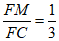 .
.
……………14分
(19)(本小题15分)
解:(I)函数f (x)的定义域为(0,+∞). ……………………1分
若a=0,则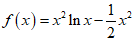 ,
,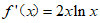 , ……………………2分
, ……………………2分
令f(x) =0.得x=1, ……………………………………3分
随x的变化,f'(x),f(x)的变化情况如下表所示
x | (0,1) | 1 | (1,+∞) |
f'(x) | – | 0 | + |
f(x) | 单调递减 | 极小值f(1) | 单调递增 |
……………5分
所以a=0时,f(x)的最小值为
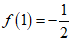 . …………6分
. …………6分
(II)因为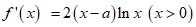 , …………7分
, …………7分
当a≤0时,x-a>0,
令f'(x)>0,得lnx>0,所以x>1,f(x)在区间(1,+∞)上单调递增,
令f'(x)<0,得lnx>0,所以0<x<1,f(x)在区间(0,1)上单调递减.
……………9分
当0<a<1时,令f’(x)=0,得x=1或x=a,
随x的变化,f'(x),f (x)的变化情况如下表所示
x | (0,a) | a | (a,1) | 1 | (1,+∞) | ||
f'(x) | + | 0 | – | 0 | + | ||
f(x) | 单调递增 | f(a) | 单调递减 | f(1) | 单调递增 | ||
所以f(x)在区间(0,a)上单调递增,在区间(a,1)上单调递减,在区间(1,+∞)上单调递增. ………………………….11分
当a=1时,因为f'(x)= 2(x-1)lnx≥0,当且仅当x=1时,f'(x)=0,
所以f(x)在区间(0,+∞)上单调递增, ……………………12分
当a>1时,令f'(x)=0,得x=1或x=a,
随x的变化,f'(x),f(x)的变化情况如下表所示
x | (0,1) | 1 | (1,a) | a | (a,+∞) |
f'(x) | + | 0 | – | 0 | + |
f(x) | 单调递增 | f(1) | 单调递减 | f(a) | 单调递增 |
所以f(x)在区间(0,1)上单调递增,在区间(1,a)上单调递减,在区间(a,+∞)上单调递增.………………………………14分
综上所述,
当a≤0时,f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1);
当0<a<1时,f(x)的单调递增区间为(0,a),(1,+∞),单调递减区间为(a,1);
当a=1时,f(x)的单调递增区间为(0,+∞),无单调递减区间;
当a>1时,f(x)的单调递增区间为(0,1),(a,+∞),单调递减区间为(1,a).
………………………………15分
20.(本小题15分)
解:(I)当直线l斜率不存在时,其方程为x=-1. ………………………………2分
由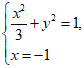 得
得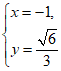 或
或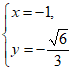 ……4分
……4分
所以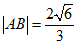 ……………………5分
……………………5分
(II)假设存在P(m,0),使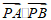 为定值,
为定值,
①当直线l斜率存在时,
设直线l的方程为:y=k(x+1),A(x1,y1),B(x2,y2), ……………………6分
由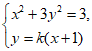
得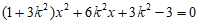 ,
,
则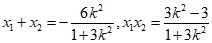 . …………………………8分
. …………………………8分
所以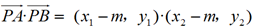
=(x1-m)(x2-m)+y1y2
=x1x2-m(x1+x2)+m2+k2(x1+1)(x2+1)
=x1x2 -m(x1+x2)+m2+k2x1x2+ k2 (x1+x2)+k2
= (k2-m)(x1+x2)+(k2+1)x1x2+k2+m2
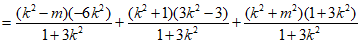
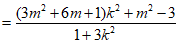 ……………………11分
……………………11分
若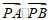 为常数,只需
为常数,只需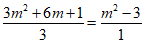 ,
,
解得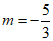 ,此时
,此时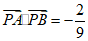 .…………………………13分
.…………………………13分
所以存在点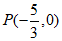 ,使
,使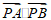 为定值
为定值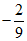 .
.
②当直线l与x轴垂直时,
不妨设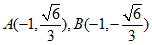 ,
,
当点P坐标为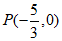 时,
时,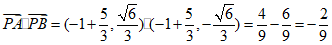 .
.
综上,存在点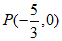 ,使
,使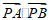 为定值
为定值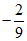 .…………………………15分
.…………………………15分
21.(本小题14分)
解:(I)因为4+1 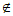 A,|4-1|
A,|4-1| 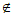 A,所以数集A不具有性质P;………………3分
A,所以数集A不具有性质P;………………3分
(II)(i)因为a2021+ a2021= 2a2021>a2021,所以a2021+a2021
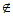 B,
B,
所以|a2021-a2021|=0∈B,则a1=0.
因为ai<ai+1(i=1,2,…,2020),
所以a2021+a2020>a2021+a2019>…>a2021+a2>a2021.
所以a2021+ai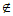 B(i=2,3,…,2020).
B(i=2,3,…,2020).
所以a2021-ai∈B(i=2,3,…,2020).
因为0<a2021-a2020<a2021-a2019<…<a2021-a2<a2021,
所以a2021-ai=a2022-i(i=2,3,…,2020).
①
所以a2021=a2020+a2,a2021=a2019+a3.
因为a2020+a2019>a2020+a2018>…>a2020+a3>a2020+a2=a2021,
所以a2020 +ai B(i=3,4,…,2019).
B(i=3,4,…,2019).
所以a2020-ai∈B(i=3,4,…,2019).
因为0<a2020-a2019<a2020-a2018<…<a2020-a3<a2020,
所以a2020-a2019=a2,a2020-a3=a2018.
否则a2020-a2019=ak(k≥3),得a2020≥a3+a2019=a2021矛盾.
a2020-a3= al(l≥2019),得a2020≥a3+a2019=a2021矛盾,
所以a2020-ai=a2021-i(i=3,…,2019).
②
①–②得a2022-i-a2021-i=a2021-a2020=a2(i=3,…,2019),
即a3-a2=a4-a3=…=a2019-a2018=a2.
所以ai+1-ai= a2(i=1,2,…,n-1).
所以a1,a2,…,an是等差数列. …………………………12分
(ii)n的最大值是4. ………………………………………………14分