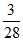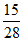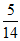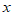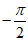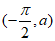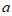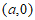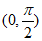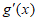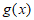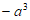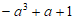本试卷共150分,考试时长120分钟。
第一部分(选择题
共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合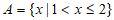 ,那么
,那么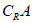 =
=
A. 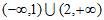 B.
B.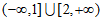
C. 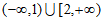 D.
D.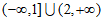
2. 已知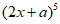 的展开式中
的展开式中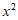 的系数为-40,那么
的系数为-40,那么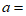
A. -2 B. -1 C. 1 D. 2
3. 已知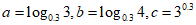 ,那么
,那么
A. 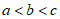 B.
B. 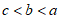 C.
C. 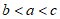 D.
D.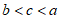
4. 已知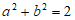 ,那么
,那么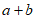 的最大值为
的最大值为
A. 1 B. 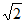 C. 2 D.
C. 2 D.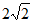
5. 在平行四边形ABCD中,已知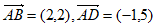 ,E为CD的中点,那么
,E为CD的中点,那么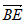 =
=
A. (-2,4) B. (-2,3) C. (-1,4) D. (-1,3)
6. 已知函数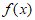 满足
满足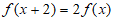 ,当
,当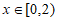 时,
时,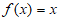 ,那么
,那么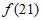 =
=
A. 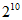 B.
B. 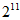 C.
C. 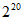 D.
D.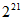
7. 某三棱柱的三视图如图所示,该三棱柱的表面积为
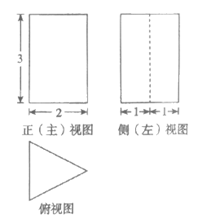
A. 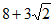 B.
B. 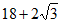 C. 22 D.
C. 22 D.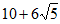
8. 已知双曲线C: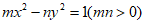 ,那么”双曲线C的渐近线为
,那么”双曲线C的渐近线为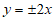 “是”
“是”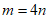 “的
“的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 在△ABC中,已知∠A=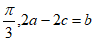 ,那么
,那么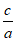 =
=
A. 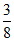 B.
B. 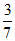 C.
C. 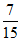 D.
D.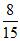
10. 有三个因素会影响某种产品的产量,分别是温度(单位:℃)、时间(单位:min)、催化剂用量(单位:g),三个因素对产量的影响彼此独立,其中温度有三个水平:80、85、90,时间有三个水平:90、120、150,催化剂用量有三个水平:5、6、7,按全面实验要求,需进行27种组合的实验,在数学上可以证明:通过特定的9次实验就能找到使产量达到最大的最优组合方案。下表给出了这9次实验的结果:
实验号 | 温度(℃) | 时间(min) | 催化剂用量(g) | 产量(kg) |
1 | 80 | 90 | 5 | 31 |
2 | 80 | 120 | 6 | 54 |
3 | 80 | 150 | 7 | 38 |
4 | 85 | 90 | 6 | 53 |
5 | 85 | 120 | 7 | 49 |
6 | 85 | 150 | 5 | 42 |
7 | 90 | 90 | 7 | 57 |
8 | 90 | 120 | 5 | 62 |
9 | 90 | 150 | 6 | 64 |
根据上表,三因素三水平的最优组合方案为
A. 85℃ 120 min 7 g B. 90℃ 120 min6 g
C. 85℃ 150 min 6 g D. 90℃ 150 min7 g
第二部分(非选择题
共110分)
二、填空题:共5小题,每小题5分,共25分。
11. 复数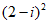 的实部为_____________。
的实部为_____________。
12. 已知直线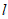 不在平面
不在平面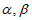 内,给出下列三个论断:
内,给出下列三个论断:
①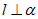 ;
;
②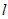 ∥
∥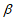 ;
;
③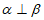 。
。
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:______________。
13. 已知抛物线C: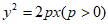 过点M(4,4),那么抛物线C的准线方程为_________,设N为平面直角坐标系xOy内一点,若线段MN的垂直平分线过抛物线C的焦点F,那么线段FN的长度为_____________。
过点M(4,4),那么抛物线C的准线方程为_________,设N为平面直角坐标系xOy内一点,若线段MN的垂直平分线过抛物线C的焦点F,那么线段FN的长度为_____________。
14. 角α的终边与单位圆的交点A位于第一象限,其横坐标为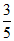 ,那么
,那么 =__________,点A沿单位圆逆时针运动到点B,所经过的弧长为
=__________,点A沿单位圆逆时针运动到点B,所经过的弧长为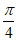 ,则点B的横坐标为___________。
,则点B的横坐标为___________。
15. 对于定义域为R的函数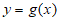 ,设关于x的方程
,设关于x的方程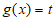 ,对任意的实数t总有有限个根,记根的个数为
,对任意的实数t总有有限个根,记根的个数为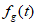 ,给出下列命题:
,给出下列命题:
①存在函数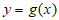 满足:
满足: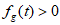 ,且
,且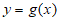 有最小值;
有最小值;
②设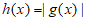 ,若
,若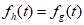 ,则
,则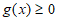 ;
;
③若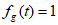 ,则
,则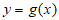 为单调函数;
为单调函数;
④设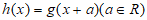 ,则
,则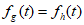 。
。
其中所有正确命题的序号为______________。
三、解答题:共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16.(本小题13分)
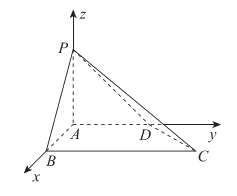
如图,四棱锥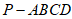 中,PA⊥平面ABCD,AB⊥BC,AD∥BC,
中,PA⊥平面ABCD,AB⊥BC,AD∥BC,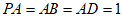 ,
,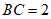 。
。
(Ⅰ)求证:AD⊥平面PAB;
(Ⅱ)求二面角 的余弦值。
的余弦值。
17.(本小题13分)
已知等比数列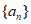 满足
满足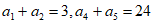 。
。
(Ⅰ)求{an}的通项公式;
(Ⅱ)从条件①、条件②这两个条件中选择一个作为已知,求数列{bn}的前n项和Sn。
条件①:设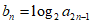 ;
;
条件②:设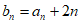 。
。
注:如果选择条件①、条件②分别解答,按第一个解答计分。
18.(本小题14分)
某市2019年一季度全市居民人均消费支出情况如下表所示,全市居民分为城镇居民和农村居民,人均消费支出分为食品烟酒、衣着、居住、生活用品及服务、交通和通信、教育文化和娱乐、医疗保健、其他用品及服务共8类。
2019年一季度
单位:元
指标名称 | 全市居民 | 城镇居民 | ||
2019年一季度 | 增速(%) | 2019年一季度 | 增速(%) | |
人均消费支出 | 10637 | 7.4 | 11440 | 7.4 |
食品烟酒 | 2292 | 8.2 | 2401 | 8.2 |
衣着 | 628 | 0.0 | 670 | -1.0 |
居住 | 3846 | 5.7 | 4200 | 5.6 |
生活用品及服务 | 546 | 6.8 | 588 | 8.3 |
交通和通信 | 1219 | 11.0 | 1303 | 10.5 |
教育文化和娱乐 | 927 | 10.5 | 1020 | 11.0 |
医疗保健 | 874 | 14.2 | 920 | 13.6 |
其他用品及服务 | 305 | 1.0 | 338 | 2.7 |
(Ⅰ)从全市居民的8类人均消费支出中随机选取1类,求这类人均消费支出超过1 000元的概率;
(Ⅱ)从城镇居民的8类人均消费支出中随机选取3类,记X表示其中不超过2 000元的类数,求X的分布列及数学期望;
(Ⅲ)请直接写出这8类人均消费支出中,农村居民人均消费支出增速大于城镇居民人均消费支出增速的类别。
19.(本小题15分)
已知函数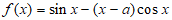 ,其中
,其中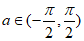 。
。
(Ⅰ)若曲线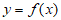 在
在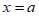 处的切线过点
处的切线过点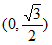 ,求a的值;
,求a的值;
(Ⅱ)若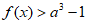 对
对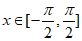 恒成立,求a的取值范围。
恒成立,求a的取值范围。
20.(本小题15分)
已知椭圆C: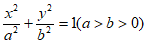 的右焦点为F,左、右顶点分别为
的右焦点为F,左、右顶点分别为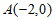 ,
,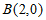 ,
,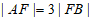 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过P(2,1)的直线l与椭圆C交于不同的两点M,N,过点N作x轴的垂线,与直线BM交于点D,E为线段DN的中点,证明:直线BE的斜率为定值。
21.(本小题15分)
设数列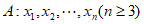 。
。
定义集合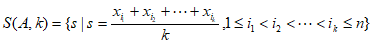 ,其中
,其中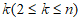 为给定的正整数。
为给定的正整数。
(Ⅰ)若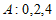 ,求
,求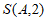 ;
;
(Ⅱ)若A中的项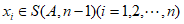 ,求证:A为常数列;
,求证:A为常数列;
(Ⅲ)记集合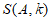 的最大元素为
的最大元素为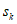 ,求证:
,求证: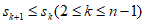 。
。
【试题答案】
一、选择题(共10小题,每小题4分,共40分)
1. D 2. B 3. C 4. C 5. A 6. A 7. D 8. C 9. B 10. B
二、填空题(共5小题,每小题5分,共25分)
11. 3 12. 若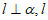 ∥
∥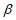 ,则
,则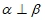 。(答案不唯一)
。(答案不唯一)
13. 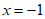 5 14.
5 14. 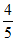
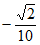 15. ②④
15. ②④
三、解答题(共6小题,共85分)
16.(本小题13分)
解:(Ⅰ)因为PA⊥平面ABCD,
所以PA⊥AD,
因为AB⊥BC,AD∥BC,
所以AB⊥AD,
又因为PA,AB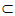 平面PAB,
平面PAB,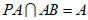 ,
,
所以AD⊥平面PAB。 5分
(Ⅱ)因为PA⊥平面ABCD,所以PA⊥AB,
由(Ⅰ)知,PA⊥AD,AB⊥AD。
如图,建立空间直角坐标系 。
。
因为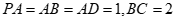 ,
,
所以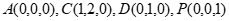 ,
,
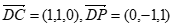 ,
,
设平面PCD的法向量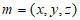 ,
,
由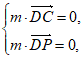 得
得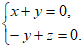
令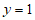 ,则
,则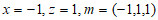 。
。
平面ABCD的法向量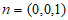 ,
,
设二面角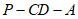 的大小为
的大小为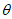 ,
,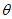 为锐角,
为锐角,
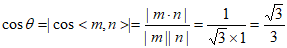 ,
,
所以二面角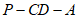 的余弦值为
的余弦值为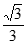 。 13分
。 13分
17.(本小题13分)
解:(Ⅰ)设等比数列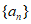 的公比为q,
的公比为q,
所以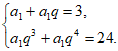 解得
解得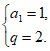
所以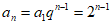 。 5分
。 5分
(Ⅱ)选择条件①: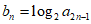 。
。
因为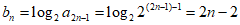 ,
,
所以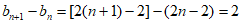 。
。
又因为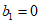 ,
,
所以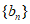 是首项
是首项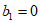 ,公差
,公差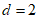 的等差数列,
的等差数列,
所以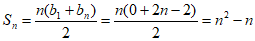 。
。
选择条件②: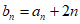 ,
,
因为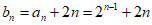 ,
,
所以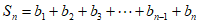
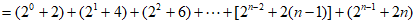
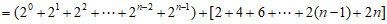
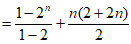
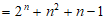 。 13分
。 13分
18. (本小题14分)
解:(Ⅰ)记事件A为“从全市居民的8类人均消费支出中随机选取1类,这类人均消费支出超过1000元“。
从全市居民的8类人均消费支出中随机选取1类,共有8种等可能的取法,其中有3类人均消费支出超过1000元。
所以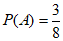 。 4分
。 4分
(Ⅱ)X所有可能的取值为1,2,3,
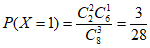 ,
,
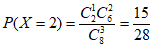 ,
,
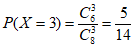 ,
,
则X的分布列为
X | 1 | 2 | 3 |
P |
|
|
|
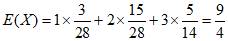 。 11分
。 11分
(Ⅲ)衣着、居住、交通和通信、医疗保健。 14分
19.(本小题15分)
解:(Ⅰ)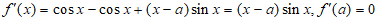 ,
,
曲线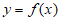 在
在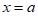 处的切线方程为
处的切线方程为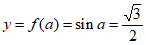 ,
,
因为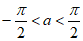 ,所以
,所以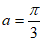 。 5分
。 5分
(Ⅱ)设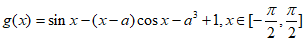 ,
,
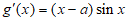 ,令
,令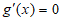 ,得
,得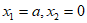 ,
,
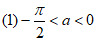 时,
时,
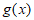 与
与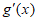 的情况如下:
的情况如下:
|
|
|
|
| 0 |
|
|
| + | + | 0 | - | 0 | + | + |
|
| ↗ | ↘ |
| ↗ |
设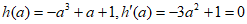 ,因为
,因为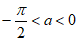 ,所以
,所以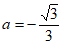 ,
,
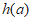 在
在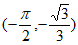 上递减,在
上递减,在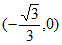 上递增,
上递增,
所以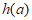 的最小值为
的最小值为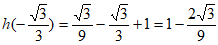 ,
,
因为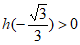 ,所以
,所以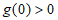 ,
,
所以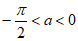 时,
时,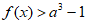 恒成立。
恒成立。
(2)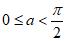 时,
时,
因为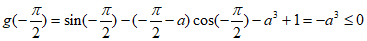 ,
,
所以当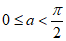 时,不等式
时,不等式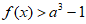 并非对
并非对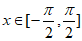 恒成立。
恒成立。
综上所述,实数a的取值范围是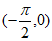 。 15分
。 15分
20. 本小题15分
解:(Ⅰ)依题意有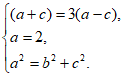
解得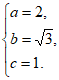
所以椭圆C的方程为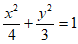 。 4分
。 4分
(Ⅱ)由题知,直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为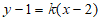 ,
,
联立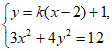 消y得
消y得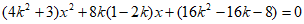 ,
,
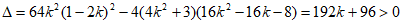 ,解得
,解得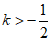 。
。
设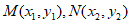 ,则
,则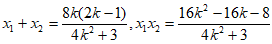 ,
,
直线BM: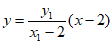 ,令
,令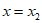 ,得
,得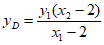 ,所以
,所以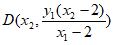 。
。
设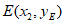 ,则
,则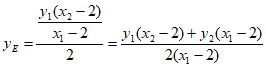 。
。
直线BE的斜率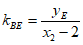
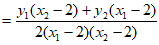
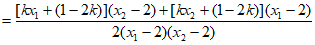
其中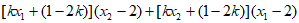
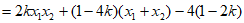
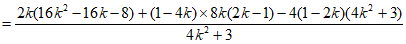
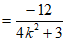 ,
,
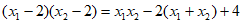
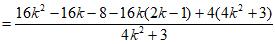
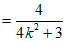
所以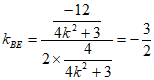 。 15分
。 15分
21. (本小题15分)
解:(Ⅰ)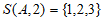 。 3分
。 3分
(Ⅱ)由于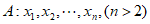 ,不妨设
,不妨设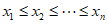 ,令
,令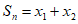 +…+
+…+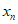 ,
,
则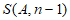 中的元素为:
中的元素为: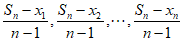 ,
,
因为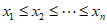 ,
,
所以有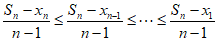 ,
,
因为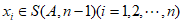 ,
,
所以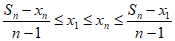 。
。
化简可得: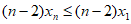 ,
,
从而可得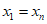 ,
,
从而数列A为常数列; 10分
(Ⅲ)对任意的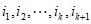 ,有
,有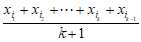
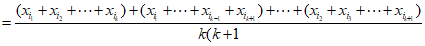
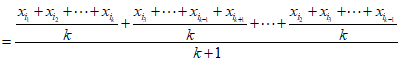
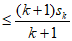
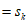 ,
,
所以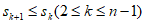 。 15分
。 15分