本试卷共三道大题,28道小题,满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
第1—8题均有四个选项,符合题意的选项只有一个。
1. 某几何体的三视图如图所示,该几何体是
A. 三棱柱 B. 正方体 C. 圆锥 D. 圆柱
2. 在平面直角坐标系xOy中,下列函数的图象不过点(1,1)的是
A. 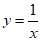 B.
B. 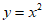 C.
C. 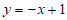 D.
D.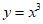
3. 2020年7月23日,中国首颗火星探测器“天问一号“成功发射。2021年2月10日,在经过长达七个月,475 000 000公里的漫长飞行之后,“天问一号“成功进入火星轨道,将475 000 000用科学记数法表示应为
A. 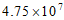 B.
B. 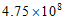 C.
C. 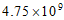 D.
D.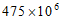
4. 一副三角板如图放置,斜边互相平行,且每个三角板的直角顶点都在另一个三角板的斜边上,在图中所标记的角中,与∠1相等的角是
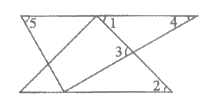
A. ∠2 B. ∠3 C. ∠4 D. ∠5
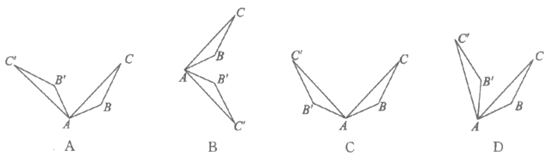
5. 如图,△ABC经过旋转或轴对称得到△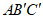 ,其中△ABC绕点A逆时针旋转60°的是
,其中△ABC绕点A逆时针旋转60°的是
6. 实数a,b,c在数轴上的对应点的位置如图所示,下列式子正确的是
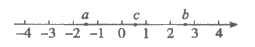
A. 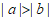 B.
B. 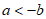 C.
C. 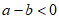 D.
D.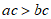
7. 如图,PA,PB是⊙O的切线,切点分别为A,B,PO的延长线交⊙O于点C,连接OA,OB,BC,若AO=2,OP=4,则∠C等于
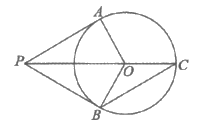
A. 20° B. 30° C. 45° D. 60°
8. 一个直角三角形木架的两条直角边的边长分别是30 cm,40 cm,现要做一个与其相似的三角形木架,如果以60 cm长的木条为其中一边,那么另两边中长度最大的一边最多可达到
A. 60 cm B. 75 cm C. 100 cm D.120 cm
二、填空题(本题共16分,每小题2分)
9. 若分式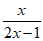 的值为0,则x的值等于_____________。
的值为0,则x的值等于_____________。
10. 分解因式: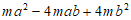 =____________。
=____________。
11. 用一组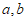 的值说明”若
的值说明”若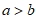 ,则
,则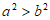 “是假命题,这组值可以是a=_______,b=_______。
“是假命题,这组值可以是a=_______,b=_______。
12. 4月23日是世界读书日,甲、乙两位同学在读书日到来之际共购买图书22本,其中甲同学购买的图书数量比乙同学购买的图书数量的2倍多1,求甲、乙两位同学分别购买的图书数量,设甲同学购买图书x本、乙同学购买图书y本,则可列方程组为_______________。
13. 有人做了掷骰子的大量重复试验,统计结果如下表所示:
投掷次数(n) | “出现点数为1″的次数(频数m) | 频率 |
300 | 52 | 0.173 |
400 | 65 | 0.163 |
500 | 80 | 0.160 |
600 | 99 | 0.165 |
700 | 114 | 0.163 |
800 | 136 | 0.170 |
900 | 151 | 0.168 |
1000 | 166 | 0.166 |
根据上表信息,掷一枚骰子,估计”出现点数为1″的概率为___________。(精确到0.001)
14. 若一个多边形的内角和是外角和的2倍,则这个多边形的边数为_____________。
15. 若关于x的一元二次方程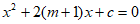 有两个相等的实数根,则c的最小值是______________。
有两个相等的实数根,则c的最小值是______________。
16. 小青要从家去某博物馆参加活动,经过查询得到多种出行方式,可选择的交通工具有地铁、公交车、出租车、共享单车等,小青的家到地铁站(或公交车站)有一段距离,地铁站(或公交车站)到该博物馆也有一段距离,需要步行或骑共享单车,共享单车的计价规则为:每30分钟1.5元,不足30分钟的按30分钟计算,出行方式的相应信息如下表(√表示某种出行方式选择的交通工具):
乘出租车 | 乘坐 公交车 | 乘坐 地铁 | 骑共享单车 | 共需步行(公里) | 总用时 (分钟) | 费用 (元) | |
方式1 | √ | 2.0 | 47 | 4 | |||
方式2 | √ | 56 | 3 | ||||
方式3 | √ | 1.6 | 78 | 3 | |||
方式4 | √ | 1.8 | 80 | 3 | |||
方式5 | √ | √ | 1.5 | 60 | 6 | ||
方式6 | √ | √ | 1.6 | 56 | 6 | ||
方式7 | √ | √ | 1.7 | 55 | 6 | ||
方式8 | √ | √ | 1.5 | 57 | 6 | ||
方式9 | √ | 0.2 | 32 | 41 |
根据表格中提供的信息,小青得出以下四个推断:
①要使费用尽可能少,可以选择方式2,3,4;
②要使用时较短,且费用较少,可以选择方式1;
③如果选择公交车和地铁混合的出行方式,平均用时约57分钟;
④如果将上述出行方式中的”步行”改为”骑共享单车”,那么除方式2外,其它出行方式的费用均会超过8元。
其中推断合理的是___________(填序号)。
三、解答题(本题共68分,第17—19题,每小题5分,第20题6分,第21—23题,每小题5分,第24—26题,每小题6分,第27—28题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 计算: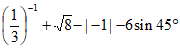 。
。
18. 已知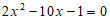 ,求代数式
,求代数式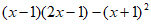 的值。
的值。
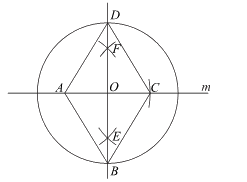
19. 尺规作图:
如图,已知线段a,线段b及其中点。
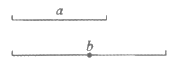
求作:菱形ABCD,使其两条对角线的长分别等于线段a,b的长。
作法:①作直线m,在m上任意截取线段AC=a;
②作线段AC的垂直平分线EF交线段AC于点O;
③以点O为圆心,线段b的长的一半为半径画圆,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的菱形。
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);

(2)完成下面的证明。
证明: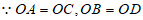 ,
,
∴四边形ABCD是______________,
∵AC⊥BD,
∴四边形ABCD是菱形(_____________________________)(填推理的依据)。
20. 解不等式组: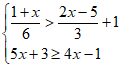 ,并写出其中的正整数解。
,并写出其中的正整数解。
21. 解分式方程: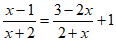 。
。
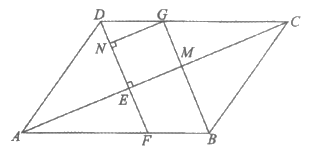
22. 如图,在平行四边形ABCD中,过点D作DE⊥AC于点E,DE的延长线交AB于点F,过点B作BG∥DF交DC于点G,交AC于点M,过点G作GN⊥DF于点N。
(1)求证:四边形NEMG为矩形;
(2)若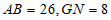 ,sin∠CAB=
,sin∠CAB=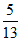 ,求线段AC的长。
,求线段AC的长。
23. 在平面直角坐标系 中,直线
中,直线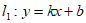 与直线
与直线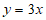 平行,且过点
平行,且过点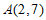 。
。
(1)求直线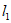 的表达式;
的表达式;
(2)横、纵坐标都是整数的点叫作整点,直线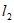 与直线
与直线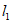 关于y轴对称,直线
关于y轴对称,直线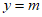 与直线
与直线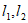 围成的区域W内(不包含边界)恰有6个整点,求m的取值范围。
围成的区域W内(不包含边界)恰有6个整点,求m的取值范围。
24. 如图,△ABC是⊙O的内接三角形,过点C作⊙O的切线交AB的延长线于点D,OE⊥BC于点E,交CD于点F。
(1)求证:∠A+∠OFC=90°;
(2)若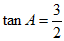 ,BC=6,求线段CF的长。
,BC=6,求线段CF的长。

25. 第24届冬季奥林匹克运动会,又称2022年北京冬奥会,将于2022年2月4日至2月20日,在北京市和张家口市同时举行,为了调查同学们对冬奥知识的了解情况,小冬从初中三个年级各随机抽取10人,进行了相关测试,获得了他们的成绩(单位:分),并对数据(成绩)进行了整理、描述和分析。下面给出了相关信息:
a. 30名同学冬奥知识测试成绩的统计图如下:

b. 30名同学冬奥知识测试成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
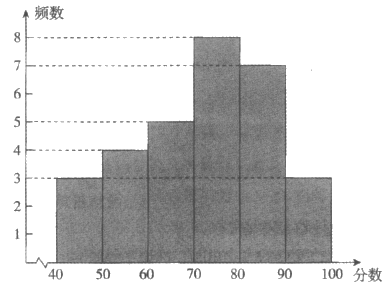
c. 测试成绩在70≤x<80这一组的是:
70 73 74 74 75 75 77 78
d. 小明的冬奥知识测试成绩为85分。
根据以上信息,回答下列问题:
(1)小明的测试成绩在抽取的30名同学的成绩中从高到低排名第__________;
(2)抽取的30名同学的成绩的中位数为__________;
(3)序号为1—10的学生是七年级的,他们的成绩的方差记为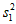 ;序号为11—20的学生是八年级的,他们的成绩的方差记为
;序号为11—20的学生是八年级的,他们的成绩的方差记为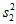 ;序号为21—30的学生是九年级的,他们的成绩的方差记为
;序号为21—30的学生是九年级的,他们的成绩的方差记为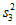 ,直接写出
,直接写出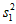 ,
,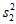 ,
,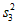 的大小关系;
的大小关系;
(4)成绩80分及以上记为优秀,若该校初中三个年级420名同学都参加测试,估计成绩优秀的同学约为____________人。
26. 在平面直角坐标系xOy中,点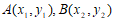 在抛物线
在抛物线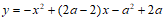 上,其中
上,其中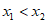 。
。
(1)求抛物线的对称轴(用含a的式子表示);
(2)①当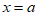 时,求y的值;
时,求y的值;
②若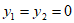 ,求
,求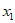 的值(用含a的式子表示);
的值(用含a的式子表示);
(3)若对于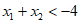 ,都有
,都有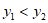 ,求a的取值范围。
,求a的取值范围。
27. 已知∠MAN=30°,点B为边AM上一个定点,点P为线段AB上一个动点(不与点A,B重合),点P关于直线AN的对称点为点Q,连接AQ,BQ,点A关于直线BQ的对称点为点C,连接PQ,CP。
(1)如图1,若点P为线段AB的中点。
①直接写出∠AQB的度数;
②依题意补全图形,并直接写出线段CP与AP的数量关系;
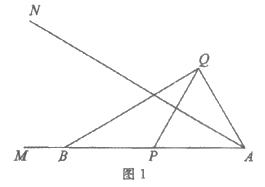
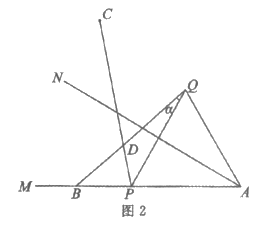
(2)如图2,若线段CP与BQ交于点D。
①设∠ ,求∠CPQ的大小(用含
,求∠CPQ的大小(用含 的式子表示);
的式子表示);
②用等式表示线段DC,DQ,DP之间的数量关系,并证明。
28. 在平面直角坐标系xOy中,已知正方形ABCD,其中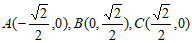 ,
,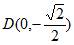 ,M,N为该正方形外两点,MN=1。
,M,N为该正方形外两点,MN=1。
给出如下定义:记线段MN的中点为P,平移线段MN得到线段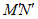 ,使点
,使点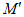 ,
,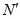 分别落在正方形ABCD的相邻两边上,或线段
分别落在正方形ABCD的相邻两边上,或线段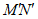 与正方形的边重合(
与正方形的边重合(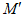 ,
,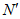 ,
, 分别为点M,N,P的对应点),线段
分别为点M,N,P的对应点),线段 长度的最小值称为线段MN到正方形ABCD的“平移距离“。
长度的最小值称为线段MN到正方形ABCD的“平移距离“。
(1)如图1,平移线段MN,得到正方形ABCD内两条长度为1的线段M1N1,M2N2,则这两条线段的位置关系是__________;若P1,P2分别为M1N1,M2N2的中点,在点P1,P2中,连接点P与点__________的线段的长度等于线段MN到正方形ABCD的“平移距离”;
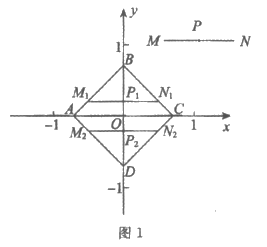
(2)如图2,已知点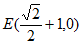 ,若M,N都在直线BE上,记线段MN到正方形ABCD的”平移距离”为d1,求d1的最小值;
,若M,N都在直线BE上,记线段MN到正方形ABCD的”平移距离”为d1,求d1的最小值;
(3)若线段MN的中点P的坐标为(2,2),记线段MN到正方形ABCD的“平移距离“为d2,直接写出d2的取值范围。
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | C | B | A | D | C | B | C |
二、填空题(本题共16分,每小题2分)
9. 0 10. 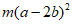 11. 0,-1(答案不唯一) 12.
11. 0,-1(答案不唯一) 12.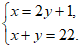
13. 0.167 14. 6 15. 0 16. ①②③
三、解答题(本题共68分,第17—19题,每小题5分,第20题6分,第21—23题,每小题5分,第24—26题,每小题6分,第27—28题,每小题7分)解答应写出文字说明、演算步骤或证明过程。
17. 解: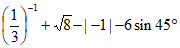
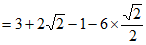 4分
4分
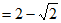 。 5分
。 5分
18. 解: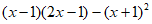
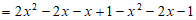 3分
3分
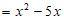 。 4分
。 4分
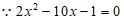 ,
,
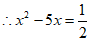 ,
,
∴原式=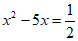 。 5分
。 5分
19. 解:(1)尺规作图如图;
(2)平行四边形; 4
对角线互相垂直的平行四边形是菱形。 5分
20. 解: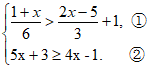
由①去分母,得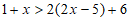 ,
,
去括号,得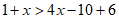 ,
,
移项,得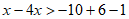 ,
,
合并同类项,得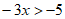 ,
,
系数化为1,得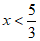 。
。
∴不等式①的解集为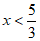 。 2分
。 2分
由②移项,得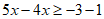 ,
,
合并同类项,得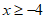 ,
,
∴不等式②的解集为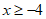 , 4分
, 4分
所以,不等式组的解集为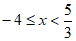 , 5分
, 5分
其中正整数解为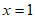 。 6分
。 6分
21. 解:去分母,得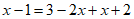 , 1分
, 1分
移项,得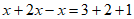 , 2分
, 2分
合并同类项,得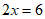 , 3分
, 3分
系数化为1,得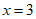 。 4分
。 4分
经检验,x=3是原方程的解,
所以,原方程的解为x=3。 5分
22. (1)证明:∵DE⊥AC,
∴∠DEC=90°,
∵BG∥DF,
∴∠GME+∠DEC=180°,
∴∠GME=90°, 1分
∵GN⊥DF,
∴∠ENG=90°,
∴四边形NEMG为矩形。 2分
(2)解:∵四边形NEMG为矩形,
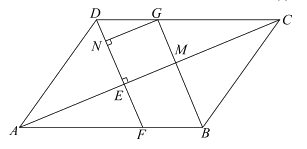
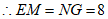 。
。
在Rt△AMB中,∠AMB=90°,
∵sin∠CAB=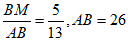 ,
,
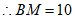 。 3分
。 3分
根据勾股定理,得AM=24,
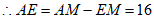 ,
,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAE=∠BCM,
∵∠AED=∠CMB=90°,
∴△ADE≌△CBM(AAS)。
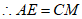 ,
,
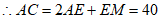 。 5分
。 5分
23. 解:(1)∵直线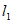 与直线
与直线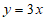 平行,
平行,
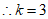 。 1分
。 1分
∵直线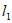 过点(2,7),
过点(2,7),
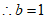 ,
,
∴直线 的表达式为
的表达式为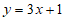 。 2分
。 2分
(2)①当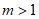 时,
时,
把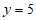 代入
代入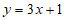 ,得
,得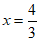 ,
,
∴直线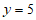 与直线
与直线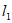 的交点为
的交点为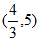 ,
,
由图形的对称性,可知
直线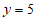 与直线
与直线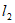 的交点为
的交点为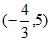 。
。
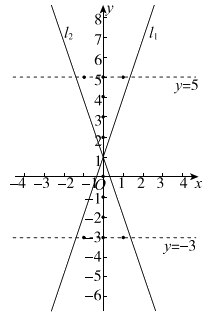
结合图象,可知
当1<m≤5时,区域W内(不包含边界)整点个数小于6,不符合题意。
当5<m≤6时,区域W内(不包含边界)恰有6个整点:
(0,2),(0,3),(0,4),(-1,5),(0,5),(1,5)。
当m>6时,区域W内(不包含边界)整点个数大于6,
不符合题意。
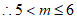 。 4分
。 4分
②当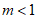 时,由图形的对称性,得
时,由图形的对称性,得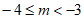 。
。
综上所述,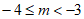 或
或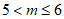 。 5分
。 5分
24. 方法1:
(1)证明:如图,作直径CG,连接BG,则∠GBC=90°。
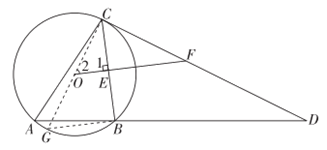
∵OE⊥BC,
∴∠1=90°=∠GBC,
∴OF∥BG,
∴∠G=∠2,
∵∠G=∠A,
∴∠A=∠2,
∵CD是⊙O的切线,
∴CG⊥CD,
∴∠OCF=90°,
∴∠2+∠OFC=90°,
∴∠A+∠OFC=90°。 3分
(2)解:∵∠G=∠A=∠2,
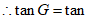 ∠2=
∠2=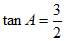 。
。
在Rt△BCG中,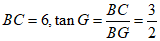 ,
,
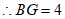 。
。
根据勾股定理,得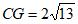 ,
,
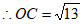 。
。
在Rt△OCF中,tan∠2=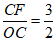 ,
,
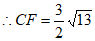 。 6分
。 6分
方法2:
(1)证明:如图,连接OC,OB,
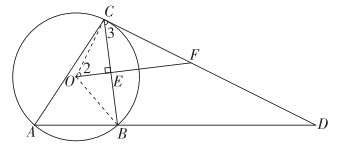
∵OE⊥BC,OB=OC,
∴∠2=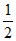 ∠BOC,
∠BOC,
∵∠A=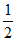 ∠BOC,
∠BOC,
∴∠A=∠2,
∵CD是⊙O的切线,
∴CO⊥CD,
∴∠2+∠OFC=90°,
∴∠A+∠OFC=90°。 3分
(2)解:∵OE⊥BC,
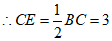 ,
,
∵∠3+∠OFC=90°,∠A+∠OFC=90°,
∴∠A=∠3,
∴tan∠3=tanA=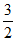 。
。
在Rt△CEF中,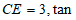 ∠3=
∠3=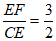 ,
,
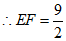 。
。
根据勾股定理,得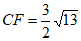 。 6分
。 6分
25. 解:(1)5; 1分
(2)74; 3分
(3)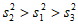 ; 5分
; 5分
(4)140。 6分
26. 解:(1)抛物线的对称轴为直线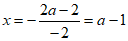 ; 2分
; 2分
(2)①当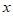
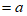 时,
时,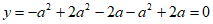 ; 3分
; 3分
②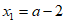 ; 4分
; 4分
(3)①当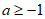 时,
时,
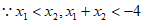 ,
,
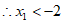 ,只需讨论
,只需讨论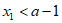 的情况,
的情况,
若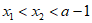 ,
,
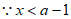 时,y随着x的增大而增大,
时,y随着x的增大而增大,
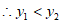 ,符合题意;
,符合题意;
若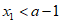
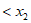 ,
,
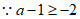 ,
,
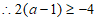 ,
,
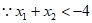 ,
,
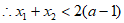 ,
,
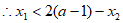 ,
,
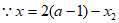 时,
时,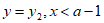 时,y随着x的增大而增大,
时,y随着x的增大而增大,
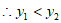 ,符合题意。
,符合题意。
②当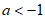 时,
时,
令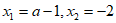 ,
,
此时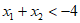 ,但
,但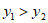 ,不符合题意;
,不符合题意;
综上所述,a的取值范围为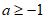 。 6分
。 6分
27. (1)解;①∠AQB=90°;
②补全图形,如图1,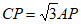 。
。
 3分
3分
(2)①解:如图2,连接CQ,
∵点P,点Q关于直线AN对称,点A,点C关于直线BQ对称,
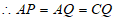 ,∠PAN=∠QAN,∠CQB=∠AQB。
,∠PAN=∠QAN,∠CQB=∠AQB。
∵∠MAN=30°,
∴∠PAQ=60°,
∴△APQ为等边三角形,
∴∠AQP=60°,PQ=AQ,
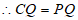 。
。
∴∠C=∠CPQ,
∵∠BQP= ,
,
∴∠CQB=60°+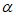 ,
,
∴∠CQP=60°+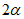 ,
,
∴∠CPQ=60°-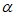 。 5分
。 5分
②结论: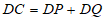 。
。
证明:∵∠CDQ=∠CPQ+∠BQP,
∴∠CDQ=60°。
在DC上截取DE=DQ,连接EQ,
∴△DEQ为等边三角形,
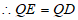 ,
,
∴∠DEQ=∠EDQ=60°,
∴∠CEQ=∠PDQ=120°,
∵∠C=∠CPQ,CQ=PQ,
∴△CEQ≌△PDQ(AAS)。
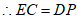 ,
,
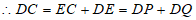 。 7分
。 7分
28. 解:(1)平行,P1; 2分
(2)如图,连接BP1,
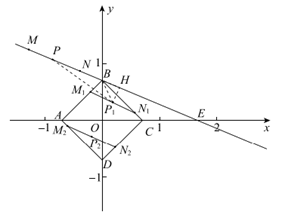
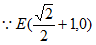 ,
,
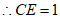 ,即
,即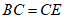 ,
,
∵∠ACB=45°,
∴∠CBE=∠CEB=22.5°,
 ∥
∥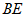 ,
,
∴∠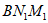 =∠
=∠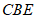 =22.5°,
=22.5°,
∵点P1为M1N1的中点,
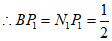 ,
,
∴∠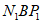 =∠
=∠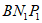 =22.5°,
=22.5°,
∴∠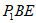 =45°,
=45°,
过点P1作P1H⊥BE于点H,则△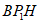 为等腰直角三角形。
为等腰直角三角形。
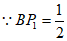 ,
,
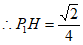 ,
,
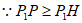 ,
,
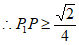 ,
,
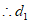 的最小值是
的最小值是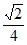 。 5分
。 5分
(3)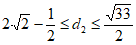 。 7分
。 7分