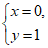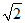北京市朝阳区2021届下学期初中九年级综合练习（一）数学试卷（一模）

本试卷共三道大题，28道小题，满分100分。考试时间120分钟。

一、选择题（本题共16分，每小题2分）

下面1-8题均有四个选项，其中符合题意的选项只有一个．

1．中国首次火星探测任务天问一号探测器在2021年2月10日成功被火星捕获，成为中国第一颗人造火星卫星，并在距离火星约11 000千米处，拍摄了火星全景图像．将11 000用科学记数法表示应为

（A）11×10³
（ B）1.1×10⁵
（C）1.1×10⁴
（ D）0.11×10⁵

2．如图是某几何体的三视图，该几何体是

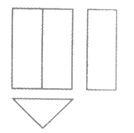
（A）长方体

（B）三棱柱

（C）三棱锥

（D）圆锥

3．如图，AB∥CD，∠A =100°，∠BCD=50°，∠ACB的度数为

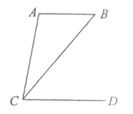
（A）25°

（B）30°

（C）45°

（D）50°

4．下列图形中，既是轴对称图形又是中心对称图形的是

（A）角
（B）等腰三角形
（C）平行四边形
（D）正六边形

5．实数a在数轴上的对应点的位置如图所示，若实数b满足a+b>0，则b的值可以是

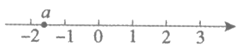
（A） -1 （B）0 （C）1 （D）2

6．一个不透明的口袋中有四张卡片，上面分别写有数字1，2，3，4，除数字外四张卡片无其他区别．随机从这个口袋中同时取出两张卡片，卡片上的数字之和等于5的概率是

（A）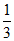
（B）

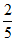
（C）

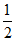
（D）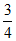

7．已知关于x的一元二次方程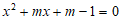有两个不相等的实数根，下列结论正确的是

（A）m≠2 （B）m>2 （C）m≥2 （D）m<2

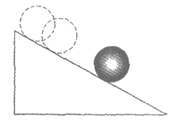
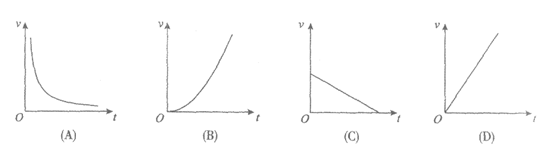
8．如图，一个小球由静止开始沿一个斜坡滚下，其速度每秒增加的值相同，用t表示小球滚动的时间，v表示小球的速度．下列图象中，能表示小球在斜坡上时v与t的函数关系的图象大致是

二、填空题（本题共16分，每小题2分）

9．若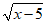在实数范围内有意义，则实数x的取值范围是____________．

10．写出一个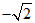比大且比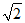小的整数____________．

11．二元一次方程组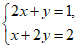的解为_________．

12．如图所示的正方形网格中，O，A，B，C，D是网格线交点，若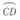与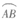所在圆的圆心都为点O，则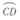与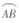的长度之比为_________．

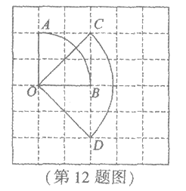
13．如图，△ABC中，BC>BA，点D是边BC上的一个动点（点D与点B，C不重合），若再增加一个条件，就能使△ABD与△ABC相似，则这个条件可以是_________（写出一个即可）．

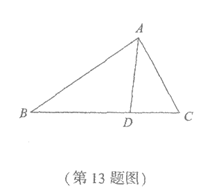
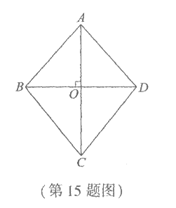
14．如图，直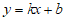线与抛物线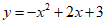交于点A，B，且点A在y轴上，点B在x轴上，则不等式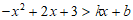的解集为_________．

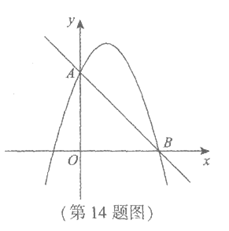
15．如图，在四边形ABCD中，AC⊥BD于点O，BO= DO．有如下四个结论：①AB= AD;②∠BAC=∠DAC;③AB=CD；④AO=CO．上述结论中，所有正确结论的序号是_________．

16．某校初三年级共有8个班级的190名学生需要进行体检，各班学生人数如下表所示：

若已经有7个班级的学生完成了体检，且已经完成体检的男生、女生的人数之比为4：3，则还没有体检的班级可能是_________．

三、解答题（本题共68分，第17-21题，每小题5分；第22题6分；第23题5分；第24-26题，每小题6分；第27-28题，每小题7分）

17．计算：．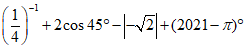

18．解不等式组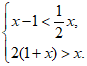

19．解方程：．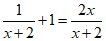

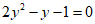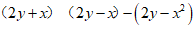20．已知，求代数式的值．

21．已知：如图，△ABC中，AB=AC，AB>BC．

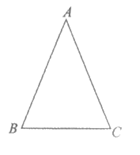
求作：线段BD，使得点D在线段AC上，且∠CBD=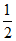∠BAC．

作法：①以点A为圆心，AB长为半径画圆：

②以点C为圆心，BC长为半径画弧，交⊙A于点P（不与点B重合）；

③连接BP交AC于点D．

线段BD就是所求作的线段．

（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；

（2）完成下面的证明．

证明：连接PC．

∵AB=AC．

∴点C在⊙A上，

∵点P在⊙A上，

∴∠CPB=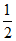∠BAC（__________________）（填推理的依据）．

∵BC=PC．

∴∠CBD=__________．

∴∠CBD=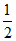∠BAC．

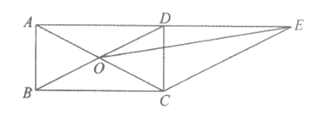
22．如图，在矩形ABCD中，对角线AC，BD相交于点O，过点C作CE∥BD，交AD的延长线于点E．

（1）求证：∠ACD=∠ECD;

（2）连接OE，若AB=2，tan∠ACD=2，求OE的长．

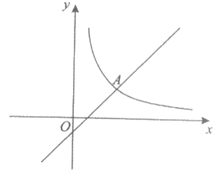
23．如图，在平面直角坐标系xOy中，A（a，2）是直线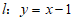与函数
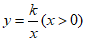的图象G的交点．

（1）①求a的值；

②求函数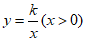的解析式．

（2）过点P（n，0）（n>0）且垂直于x轴的直线与直线l和图象G的交点分别为M，N，当S_△OPM>S_△OPN时，直接写出n的取值范围．

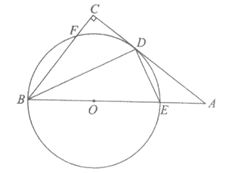
24．如图，△ABC中，∠C=90°，点E在AB上，以BE为直径的⊙O与AC相切于点D．与BC相交于点F，连接BD，DE．

（1）求证：∠ADE=∠DBE；

（2）若sinA=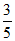，BC=6，求⊙O的半径．

25．某地农业科技部门积极助力家乡农产品的改良与推广，为了解甲、乙两种新品橙子的质量，进行了抽样调查．在相同条件下，随机抽取了甲、乙各25份样品，对大小、甜度等各方面进行了综合测评，并对数据进行收集、整理、描述和分析，下面给出了部分信息．

a．测评分数（百分制）如下：

甲 77 79 80 80 85 86 86 87 88 89 89 90 91 91 91 91 91

92 93 95 95 96 97 98 98

乙69 79 79 79 86 87 87 89 89 90 90 90 90 90 91 92 92

92 94 95 96 96 97 98 98

b．按如下分组整理、描述这两组样本数据：

c．甲、乙两种橙子测评分数的平均数、众数、中位数如下表所示：

根据以上信息，回答下列问题：

（1）写出表中m，n的值；

（2）记甲种橙子测评分数的方差为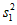，乙种橙子测评分数的方差为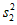，则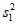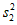，的大小关系为__________；

（3）根据抽样调查情况，可以推断_________种橙子的质量较好，理由为_________．

（至少从两个不同的角度说明推断的合理性）

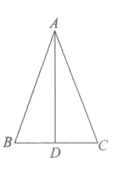
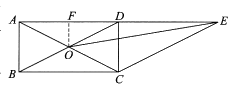
26．如图，在等腰三角形ABC中，∠BAC<60°，AB=AC，D为BC边的中点，将线段AC绕点A逆时针旋转60°得到线段AE，连接BE交AD于点F．

（1）依题意补全图形；

（2）求∠AFE的度数；

（3）用等式表示线段AF，BF，EF之间的数量关系，并证明．

27．在平面直角坐标系xOy中，抛物线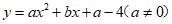的对称轴是直线x=1．

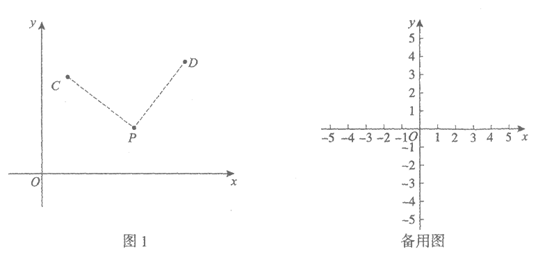
（1）求抛物线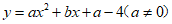的顶点坐标；

（2）当-2≤x≤3时，y的最大值是5，求a的值；

（3）在（2）的条件下，当t≤x≤t+1时，y的最大值是m，最小值是n，且m-n=3，求t的值．

28．对于平面直角坐标系xOy中的图形M和点P，给出如下定义：将图形M绕点P顺时针旋转90°得到图形N，图形N称为图形M关于点P的“垂直图形“．例如，图1中点D为点C关于点P的“垂直图形“．

（1）点A关于原点O的“垂直图形“为点B．

①若点A的坐标为（0，2），则点B的坐标为__________________；

②若点B的坐标为（2，1），则点A的坐标为__________________．

（2）E（-3，3），F（-2，3），G（a，0）．线段EF关于点G的“垂直图形“记为E’F’，点E的对应点为E’，点F的对应点为F’．

①求点E’的坐标（用含a的式子表示）；

②若⊙O的半径为2，E’F’上任意一点都在⊙O内部或圆上，直接写出满足条件的EE’的长度的最大值．

参考答案

一、选择题（本题共16分，每小题2分）

二、填空题（本题共16分，每小题2分）

三、解答题（本题共68分，第17-21题，每小题5分；第22题6分；第23题5分；第24-26题，每小题6分；第27-28题，每小题7分）

17．解：原式=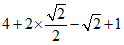…………………………………………4分

=5．…………………………………………………………5分

18．解：原不等式组为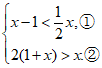

解不等式①，得x<2． …………………………………………………………2分

解不等式②，得x>-2．……………………………………………………………………4分

∴原不等式组的解集为-2<x<2． ………………………………………………5分

19．解：去分母，得

1+x+2=2x． …………………………………………………………2分

解得x=3．…………………………………………………………………………4分

经检验，x=3是原方程的解．…………………………………………………………5分

所以原方程的解是x=3．

20．解：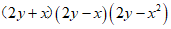

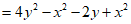………………………………2分

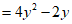，……………………………………3分

∵，

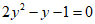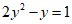∴．……………………………………………………………4分

∴原式=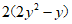

=2 …………………………………5分

21．解：（1）补全图形，如下图

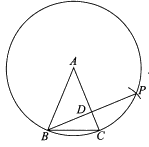…………………………………………3分

（2）一条弧所对的圆周角等于它所对的圆心角的一半． …………………4分

∠CPB． ……………………………………5分

22．（1）证明：∵四边形ABCD是矩形，

∴AC=BD,∠ADC=90°，BC∥DE． ……………………………………1分

∵CE∥BD．

∴四边形BCED是平行四边形 ……………………………2分

∴BD= CE

∴AC=CE

∴∠ACD=∠ECD………………………………………………3分

（2）解：过点O作OF⊥AD于点F，则F为AD的中点……………………4分

∵AB=2，tan∠ACD=2．

∴OF=1，EF=6． ………………………………………5分

∴OE=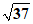……………………………………………6分

23．解：（1）①∵点A（a，2）在直线y=x-1上，

∴a=3…………………………………………………1分

②∵点A（3，2）在函数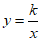
（x>0）的图象上，

∴k=6 ………………………………………………2分

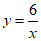∴………………………………………3分

（2）n>3．………………………………………………-5分

24．（1）证明：连接OD．

∵AC是⊙O的切线，

∴∠ODA=90°．………………………………1分

∴∠ODE+∠ADE=90°．

∵BE是⊙O的直径，

∴∠BDE=90°． …………………………………2分

∴∠BDO+∠ODE=90°．

∵DB=OD．

∴∠DBE=∠BDO．

∴∠ADE=∠DBE．…………………………………3分

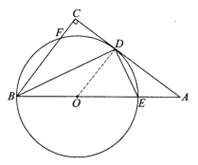
（2）解：在Rt△ACB中，∠C=90°,BC=6．

∵,

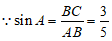∴AB=10．………………………………………………4分

设⊙O半径OB=OD=r,则AO=10-r．

∵OD⊥AC,

∴OD∥BC．

∴△AOD∽△ABC．

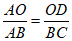∴……………………………………5分

即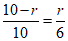

解得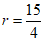…………………………………………6分

∴
⊙O的半径为．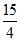

25．解：（1）m=91，n= 90． ……………………………………………………2分

（2）
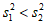………………………………………………………………4分

（3）答案不惟一，理由须支撑推断结论，………………………………………………6分

26．（1）解：依题意补全图形，如图，

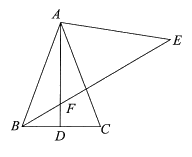…………………………………………2分

（2）解：∵AB=AC，D为BC边的中点．

∴∠BAD=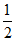∠BAC．

∵线段AC绕点A逆时针旋转60°得到线段AE，

∴AB=AE,∠CAE= 60°

∴
∠ABE=∠E

在△ABE中，∠ABE+∠E+∠BAC=180°-∠CAE=120°．

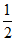∴（∠ABE+∠E+∠BAC）=60°．

即∠ABE+∠BAD= 60°

∴∠AFE=∠ABE+∠BAD=60°． …………………………4分

（3）AF+BF=EF．

证明：如图，在EF上取点M，使EM=BF，连接AM.

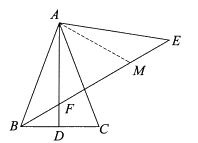
可知△ABF≌△AEM．

∴AF=AM．

∴△AFM是等边三角形

∴FM=AF

∴AF+BF=EF………………………………………………… 6分

27．解：（1）∵对称轴是直线x=1．

∴

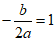
∴b=-2a……………………………………………………1分

∴

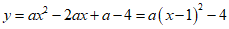
∴顶点坐标为（1．-4） …………………………2分

（2）∵当-2≤x≤3时，y的最大值是5，

∴抛物线的顶点为图象的最低点

∴当x=-2时，y=5………………………………3分

代入解析式，求得a=1． ………………………………………………4分

（3）①当t≤1≤t+1时，n=-4，m的最大值为-3．

此时m-n=1．

不符合题意，舍去

②当t+1<1，即t<0时，

．

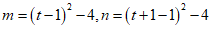∵m-n=3，

∴t=-1．

③当t>1时，

同理可得t=2．

综上所述，t=-1或t=2． ………………………………………………7分

28．解：（1）①（2，0）；…………………………………………………………1分

②（-1,2）………………………………………………………………2分

（2）①如图，过点E作EH⊥x轴于点H，过点E’作E’Q⊥x轴于点Q．

由题意可知，EG=E’G, ∠EGE’=90°．

∴△EHG≌△GQE’．…………………………………………………………3分

∴EH=GQ，HG=QE’．

∵E（-3，3），G（a，0），

∴H（-3，0）．

∴ HG=QE’=|a+3| ,EH=GQ=3． …………………………………………4分

∴OQ=|a+3|．

∴E’（a+3，a+3）．…………………………………………5分

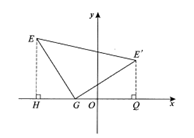
②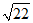.…………………………………………7分