本试卷有三道大题,考试时长120分钟,满分150分。
一、选择题(每小题4分,共40分,每题均只有一个正确答案)
1. 已知角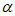 终边上一点
终边上一点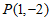 ,则
,则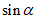 的值是
的值是
A. 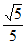 B.
B. 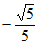 C.
C. 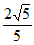 D.
D.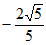
2. 已知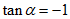 ,且
,且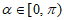 ,则
,则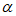 的值等于
的值等于
A. 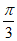 B.
B. 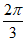 C.
C. 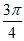 D.
D.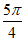
3. 若一个扇形的半径变为原来的2倍,而弧长也变为原来的2倍,则
A. 扇形的面积不变 B. 扇形的圆心角不变
C. 扇形的面积增大到原来的2倍 D. 扇形的圆心角增大到原来的2倍
4. 函数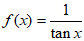 的定义域为
的定义域为
A. 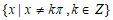 B.
B.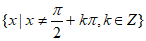
C. 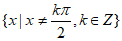 D.
D.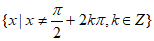
5. 函数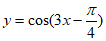 的图像可以由函数
的图像可以由函数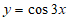 的图像如何变换得到
的图像如何变换得到
A. 向左平移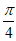 个单位 B. 向右平移
个单位 B. 向右平移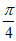 个单位
个单位
C. 向左平移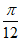 个单位 D. 向右平移
个单位 D. 向右平移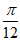 个单位
个单位
6. 设函数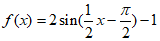 ,下列命题正确的是
,下列命题正确的是
A. 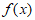 的周期是
的周期是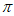 B.
B. 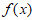 是非奇非偶函数
是非奇非偶函数
C. 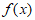 在区间
在区间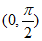 上单调递减 D.
上单调递减 D. 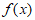 的图像关于直线
的图像关于直线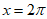 对称
对称
7. 函数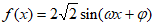 (其中
(其中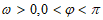 )的部分图像如图所示,则
)的部分图像如图所示,则
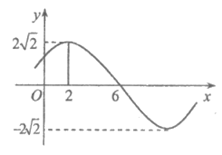
A. 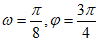 B.
B.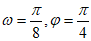
C. 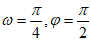 D.
D.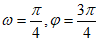
8. 如图,网格纸上小正方形的边长为1,从A,B,C,D四点中任取两个点作为向量b的始点和终点,则a·b的最大值为
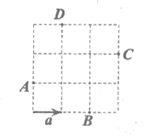
A. 1 B. 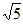 C. 3 D.
C. 3 D.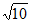
9. “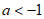 “是”
“是”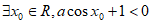 “的
“的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
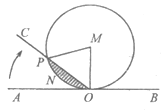
10. 如图,半径为1的⊙M切直线AB于点O,射线OC从OA出发,绕着点O,顺时针方向旋转到OB,在旋转的过程中,OC交⊙M于点P,记∠PMO=x,弓形PNO(阴影部分)的面积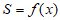 ,那么
,那么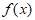 的图像是
的图像是
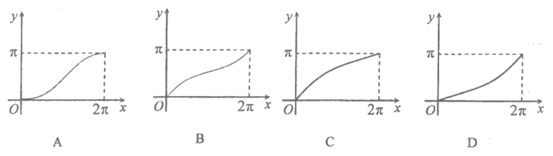
二、填空题(每小题5分,共25分)
11. 已知 ,且
,且 终边在第二象限,则
终边在第二象限,则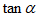 =___________。
=___________。
12. 已知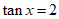 ,则
,则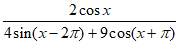 =________________。
=________________。
13. 已知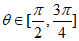 ,且
,且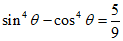 ,则
,则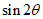 的值为___________。
的值为___________。
14. 已知向量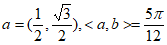 ,写出一个符合条件的b=___________。
,写出一个符合条件的b=___________。
15. 关于函数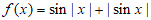 有下述四个结论:
有下述四个结论:
①f(x)是偶函数;
②f(x)是周期函数;
③f(x)在区间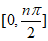 上恰有
上恰有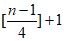 个最大值点,其中
个最大值点,其中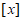 表示不超过x的最大整数;
表示不超过x的最大整数;
④当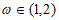 时,函数
时,函数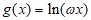 与函数
与函数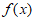 的图像恰有一个交点;
的图像恰有一个交点;
其中正确的是_________________。
(注:全部正确得5分,有漏选得3分,有错选或不选得0分)
三、解答题(共6小题,共85分。解答时写出文字说明,演算步骤或证明过程)
16. (本小题14分)
设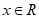 ,向量
,向量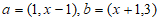 。
。
(Ⅰ)若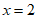 ,求
,求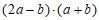 ;
;
(Ⅱ)若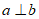 ,求x的值;
,求x的值;
(Ⅲ)若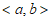 为钝角,求x的取值范围。
为钝角,求x的取值范围。
17. (本小题14分)
已知函数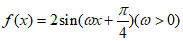 的最小正周期为
的最小正周期为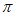 。
。
(Ⅰ)求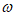 的值;
的值;
(Ⅱ)求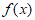 的单调递增区间。
的单调递增区间。
18、
(本小题14分)
已知函数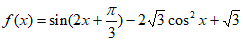 。
。
(Ⅰ)求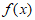 图像的对称中心;
图像的对称中心;
(Ⅱ)若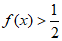 ,求x的取值范围;
,求x的取值范围;
(Ⅲ)当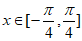 时,恒有
时,恒有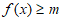 ,求m的取值范围。
,求m的取值范围。
19.(本小题14分)
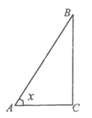
如图,在Rt△ABC中,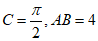 ,设
,设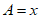 ,△ABC的面积为S。
,△ABC的面积为S。
(Ⅰ)求S关于x的函数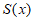 ;
;
(Ⅱ)当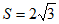 时,求x的值;
时,求x的值;
(Ⅲ)设函数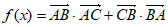 ,若方程
,若方程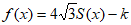 恰有两个不等实根,求实数k的取值范围。
恰有两个不等实根,求实数k的取值范围。
20. (本小题14分)一架飞机从北京向南飞行1080千米到达武汉,在武汉天河机场上空的等待航线为一个圆周,飞机通过机场上空后向南偏西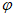 弧度
弧度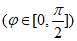 方向继续飞行20千米后,开始在一直径为40千米的圆周上顺时针飞行。已知飞机每12分钟飞行一周,将飞机等待过程中与北京的距离记作f(t),其中t为时间(单位:分),f(t)可用AD近似表示(如图)。
方向继续飞行20千米后,开始在一直径为40千米的圆周上顺时针飞行。已知飞机每12分钟飞行一周,将飞机等待过程中与北京的距离记作f(t),其中t为时间(单位:分),f(t)可用AD近似表示(如图)。
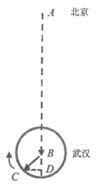
(Ⅰ)写出f(t)的解析式;
(Ⅱ)当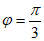 时,在等待过程中
时,在等待过程中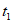 与
与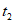 时刻飞机与北京的距离均为1070千米,求
时刻飞机与北京的距离均为1070千米,求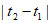 的最小值;
的最小值;
(Ⅲ)若当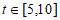 时,飞机与北京的距离越来越远,求
时,飞机与北京的距离越来越远,求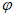 的取值范围。
的取值范围。
21. (本小题15分)高中学习的函数可视为一种实数到实数的变换,如对于函数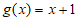 ,根据对应关系,将x变换成
,根据对应关系,将x变换成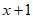 。类似地,还可以对函数进行变换,如F变换可将一类函数
。类似地,还可以对函数进行变换,如F变换可将一类函数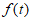 变换成一列数组:
变换成一列数组: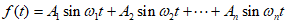
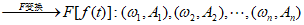 ,设
,设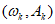 为这列数组的通式,其中
为这列数组的通式,其中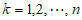 。
。
(Ⅰ)设函数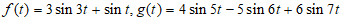 ,分别写出
,分别写出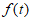 和
和 经F变换后得到的数组;
经F变换后得到的数组;
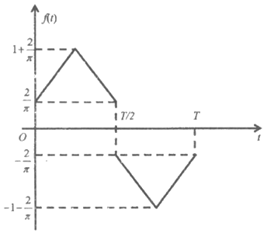
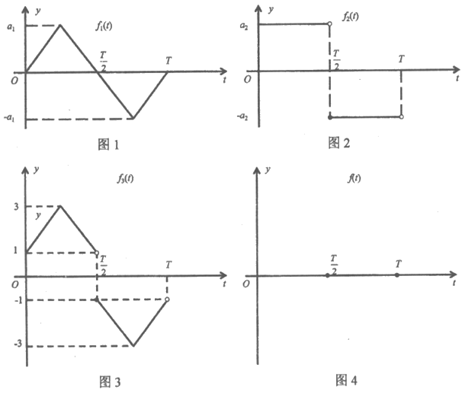
(Ⅱ)已知任意周期函数都可以分解成不同周期的正弦型函数的线性叠加,如图1所示的周期为T的函数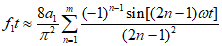 ,图2所示的周期为T的函数
,图2所示的周期为T的函数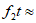
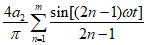 ,其中
,其中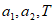 为常数,
为常数,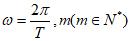 足够大。
足够大。
(i)求图3所示的周期为T的函数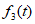 经F变换后得到的数组的通式
经F变换后得到的数组的通式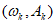 。
。
(ii)若周期为T的函数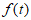 经F变换后得到的数组的通式
经F变换后得到的数组的通式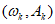 满足:
满足:
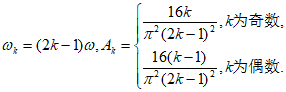
试在图4中画出f(t)在区间[0,T)上的图像(需参照图3标注出关键点),并说明理由。
【试题答案】
一、选择题(每小题4分,共40分,每题均只有一个正确答案)
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
D | C | B | C | D | D | B | C | A | A |
二、填空题(每小题5分,共25分)
11. 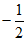 12. -2 13.
12. -2 13. 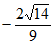 14.
14. 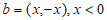
不唯一
15. ①③④(注:全部正确得5分,有漏选得3分,有选错或不选得0分)
三、解答题(共5小题,共85分。解答时写出文字说明,演算步骤或证明过程)
16. (本小题14分)
(Ⅰ)解:因为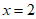 ,所以
,所以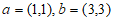 ,
,
所以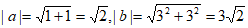
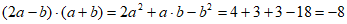 ;
;
(Ⅱ)因为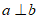 ,所以
,所以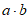 =
=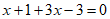 ,所以
,所以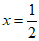 ;
;
(Ⅲ)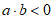 ,且
,且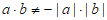 ,即
,即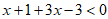 且
且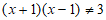
所以
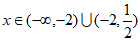 。
。
17.(本小题14分)
(Ⅰ)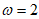 ;(Ⅱ)
;(Ⅱ)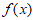 的单调递增区间为
的单调递增区间为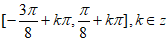 。
。
18.(本小题14分)
(Ⅰ)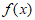 的对称中心为
的对称中心为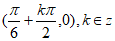 ;
;
(Ⅱ)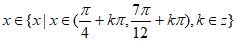 的取值范围;
的取值范围;
(Ⅲ)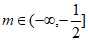 。
。
19.(本小题14分)
(Ⅰ)解:在Rt△ABC中,∠C=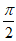 ,AB=4,设∠A=x
,AB=4,设∠A=x
所以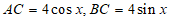 ,
,
所以△ABC的面积
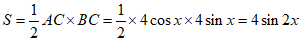 ,
,
所以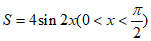
(Ⅱ)解:因为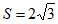
所以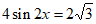 即
即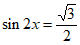
又因为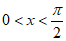 ,所以
,所以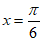 或
或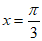
(Ⅲ)解: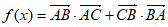
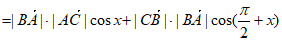
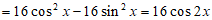 ,
,
所以
由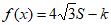 得
得
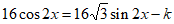
所以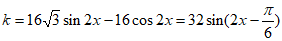
因为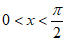
所以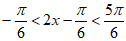
方程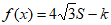 恰有两个不等实根
恰有两个不等实根
所以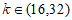 。
。
20.(本小题14分)
(Ⅰ)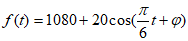
(Ⅱ)4分钟;
(Ⅲ)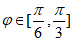 。
。
21. (本小题15分)
(Ⅰ)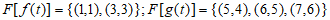
(Ⅱ)设图3的图象为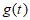 ,则当
,则当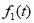 中的
中的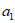 为2,当
为2,当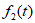 中的
中的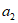 为1时,
为1时,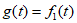 +
+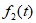 ,
,
代入数据有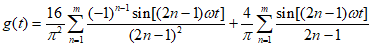 ,因此有
,因此有
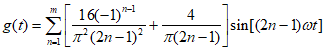
因此经F变换后的数组通项为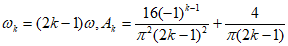 。
。
(Ⅲ)取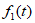 中的
中的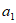 为1,取
为1,取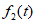 中的
中的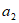 为
为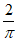 时,则设
时,则设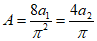 ,那么
,那么
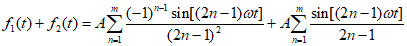
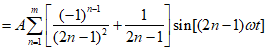
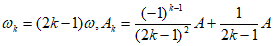
当n为奇数的时候

当n为偶数的时候
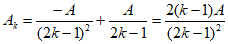
经F变换后与已知结果一致,故图象为