本试卷共四道大题,28小题,满分100分。考试时间120分钟。
一、选择题(本题共10小题,每小题3分,共30分)
下面各题均有四个选项,其中只有一个是符合题意的。
1. 下列各组数据中的三个数,可以作为直角三角形三边长的是( )
A. 1,2,3 B. 2,4,7 C. 6,8,10 D.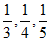
2. 下列关于矩形的说法中正确的是( )
A. 对角线相等的四边形是矩形 B. 矩形的对角线相等且互相平分
C. 对角线互相平分的四边形是矩形 D. 矩形的对角线互相垂直且平分
3. 如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )
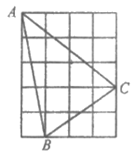
A. 0 B. 1 C. 2 D. 3
4. 下列选项中,能判定四边形ABCD是平行四边形的是( )
A. AB∥CD,AD=BC B. ∠A=∠D,∠B=∠C
C. AB∥CD,∠A+∠B=180° D. ∠A=∠C,∠B+∠D=180°
5. 某公司员工2018年的人均年收入为18万元,2020年的人均年收入为23万元,设年平均增长率为x,根据题意,可列出方程为( )
A. 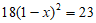 B.
B.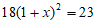
C. 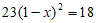 D.
D.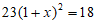
6. 在菱形ABCD中,E、F分别是BC和CD的中点,且AE⊥BC,AF⊥CD,那么∠EAF等于( )
A. 45° B. 55° C. 60° D. 75°
7. 关于x的一元二次方程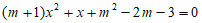 有一根是0,则m的值为( )
有一根是0,则m的值为( )
A. 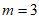 或
或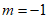 B.
B. 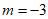 或
或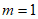
C. 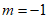 D.
D.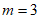
8. 小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为图2(1)所示的菱形,并测得∠B=60°,接着活动学具成为图2(2)所示的正方形,并测得对角线AC=40 cm,则图2(1)中对角线AC的长为( )
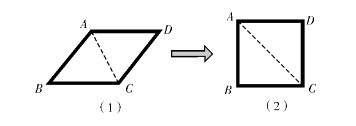
A. 20cm B. 30cm C. 40cm D. 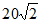 cm
cm
9. 如图,在平行四边形ABCD中,AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
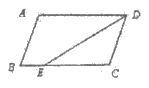
A. 2cm B. 4cm C. 6cm D.8cm
10. 定义新运算:对于两个不相等的实数a,b,我们规定符号max{a,b}表示a,b中的较大值,如: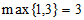 ,因此,
,因此,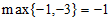 ;按照这个规定,若
;按照这个规定,若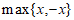
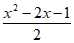 ,则x的值是( )
,则x的值是( )
A. -1 B. -1或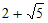 C.
C. 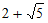 D. 1或
D. 1或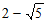
二、填空题(本题共8小题,每小题2分,共16分)
11. 已知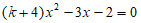 是关于x的一元二次方程,则k的取值范围是___________。
是关于x的一元二次方程,则k的取值范围是___________。
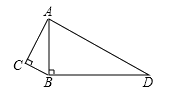
12. 如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD=____________。
13. 方程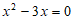 的根为__________________。
的根为__________________。
14. 已知命题:“如果两个三角形全等,那么这两个三角形的面积相等。“写出它的逆命题:____________,该逆命题是__________(填“真“或“假“)命题。
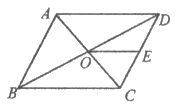
15. 如图,平行四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是____________cm。
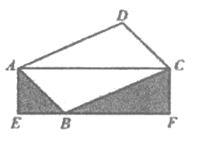
16. 如图,平行四边形ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合,若△ACD的面积3,则图中阴影部分两个三角形的面积和为____________。
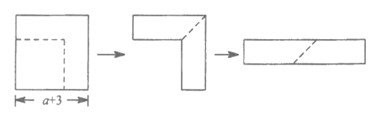
17. 如图,从边长为(a+3)的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(无重叠无缝隙),则拼成的长方形的两条边长分别是___________,面积是____________。
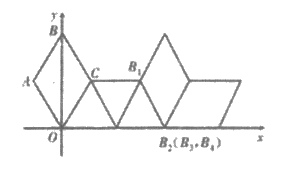
18. 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2022次,点B的落点依次为B1,B2,B3,…,则B2022的坐标为_____________。
三、解方程(本题共4小题,每小题4分,共16分)
19. 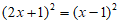 20.
20.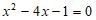
21. 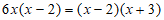 22.
22.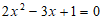
四、解答题(本题共38分,第23、24小题,每小题5分,第25、26小题,每小题6分,第27、28小题,每小题8分)
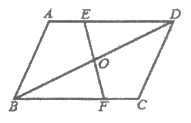
23. 如图,在平行四边形ABCD中,点E、F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证OE=OF。
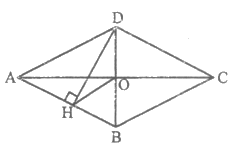
24. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连OH接,求证:∠DHO=∠DCO。
25. 已知关于x的一元二次方程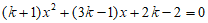 。
。
(1)讨论此方程根的情况;
(2)若方程有两个整数根,求正整数k的值。
26. 如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别为点E,F,且BE=DF。
(1)求证:四边形ABCD是菱形;
(2)连接EF并延长,交AD的延长线于点G,若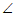 CEG=30°,AE=4,求EG的长。
CEG=30°,AE=4,求EG的长。
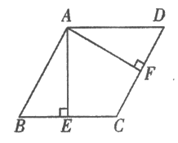
27. 已知:如图,正方形ABCD边长为4,点E为边BC上的一动点(点E可以与点B、点C重合),将线段AE绕点E顺时针旋转∠B的度数,得到线段EF,过点F作FG⊥BC交BC的延长线于点G,连接CG。
(1)如图1,依题意补全图形;
(2)证明:△FCG是等腰直角三角形;
(3)分别取AE和EF的中点M,N,连接MN,直接写出线段MN的最大值和最小值;
(4)如图2,将题目中的正方形换成边长为4的菱形,其中∠B=120°,在(3)的条件下,直接写出线段MN的最大值和最小值。
28. 在平面直角坐标系xOy中,对于两个点P,Q和图形W,如果在图形W上存在点M,N(M,N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对相好点。
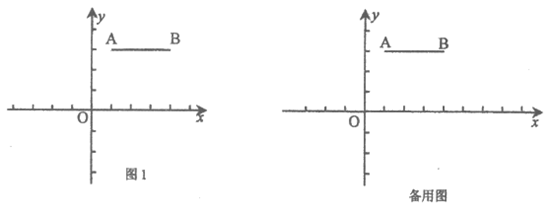
(1)如图1,已知点A(1,3),B(4,3)。
①设点O与线段AB上一点的距离为d,则d的最小值为___________,最大值为___________。
②在P1(2.5,0),P2(2,4),P3(-2,0)这三个点中,与点O是线段AB的一对相好点的是_____________。
(2)直线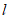 平行AB所在的直线,且线段AB上任意一点到直线
平行AB所在的直线,且线段AB上任意一点到直线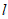 的距离都是1,若点C(x,y)是直线
的距离都是1,若点C(x,y)是直线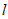 上的一动点,且点C与点O是线段AB的一对相好点,求x的取值范围。
上的一动点,且点C与点O是线段AB的一对相好点,求x的取值范围。
【试题答案】
一、选择题(共10小题,每小题3分,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | B | C | C | B | C | D | D | A | B |
二、填空题(共8小题,每小题2分,共16分)
11. 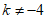 12. 13 13.
12. 13 13.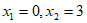
14. 逆命题:如果两个三角形的面积相等,那么这两个三角形全等;假命题。
15. 8 16. 3 17. 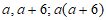 18.
18.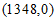
三、解方程(本题共4小题,每小题4分,共16分)
19. 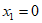 或
或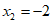 20.
20. 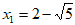 或
或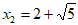
21. 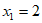 或
或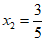 22.
22. 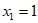 或
或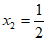
23. 略;
24. 略;
25. (1)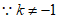 ,
,
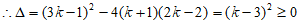
∴方程总有两个实数根。
(2)由求根公式,得: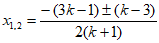
即: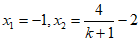 ,
,
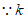 为正整数,
为正整数,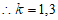 。
。
26.(1)略;(2)8
27. (1)略;
(2)提示:先证明Rt△ABE≌Rt△EGF;得到: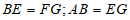 ,
,
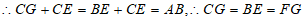 ,即证;
,即证;
(3)最小值为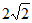 ,最大值为4;
,最大值为4;
(4)最小值为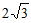 ,最大值为6。
,最大值为6。
28. (1)①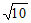 ;5;②
;5;②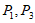 ;
;
(2)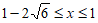 或
或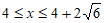 。
。
