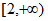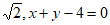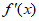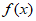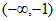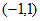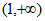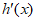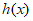(试卷满分为150分,考试时间为120分钟)
一、选择题(本大题共10小题,每小题4分,共40分)
1. 已知全集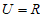 ,集合
,集合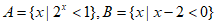 ,则
,则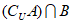 =( )
=( )
A. 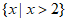 B.
B. 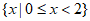 C.
C. 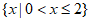 D.
D.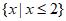
2. 下列命题中的假命题是( )
A. 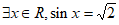 B.
B.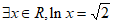
C. 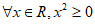 D.
D.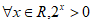
3. 已知向量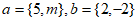 ,若
,若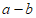 与b共线,则实数m=
与b共线,则实数m=
A. -1 B. 1 C. 2 D. -5
4. 已知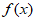 是R上的奇函数,当
是R上的奇函数,当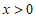 时,
时,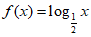 ,则
,则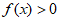 的解集是( )
的解集是( )
A. (-1,0) B. (0,1) C. 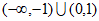 D.
D.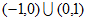
5. 将函数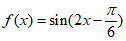 的图象向左平移
的图象向左平移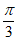 个单位长度,得到函数
个单位长度,得到函数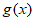 的图象,则
的图象,则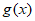 =( )
=( )
A. 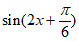 B.
B. 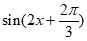 C.
C. 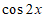 D.
D.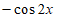
6. 若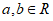 ,且
,且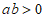 ,则下列不等式中,恒成立的是( )
,则下列不等式中,恒成立的是( )
A. 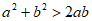 B.
B. 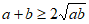 C.
C. 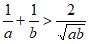 D.
D.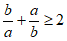
7. 已知三角形ABC,那么”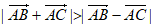 “是”三角形ABC为锐角三角形”的( )
“是”三角形ABC为锐角三角形”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
8. 声音的等级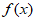 (单位:dB)与声音强度x(单位:
(单位:dB)与声音强度x(单位: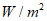 )满足
)满足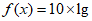
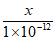 ,喷气式飞机起飞时,声音的等级约为140dB;一般说话时,声音的等级约为60dB,那么喷气式飞机起飞时声音强度约为一般说话时声音强度的( )
,喷气式飞机起飞时,声音的等级约为140dB;一般说话时,声音的等级约为60dB,那么喷气式飞机起飞时声音强度约为一般说话时声音强度的( )
A. 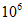 倍 B.
倍 B. 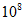 倍 C.
倍 C. 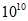 倍 D.
倍 D. 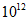 倍
倍
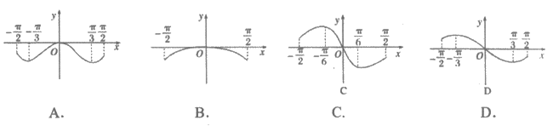
9. 函数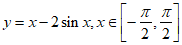 的大致图象是( )
的大致图象是( )
10. 已知函数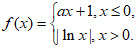 给出下列三个结论:
给出下列三个结论:
①当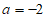 时,函数
时,函数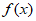 的单调递减区间为
的单调递减区间为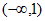 ;
;
②若函数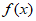 无最小值,则a的取值范围为
无最小值,则a的取值范围为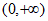 ;
;
③若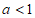 且
且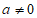 ,则
,则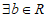 ,使得函数
,使得函数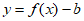 恰有3个零点
恰有3个零点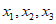 ,且
,且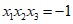 。
。
其中,所有正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
二、填空题(本大题共5小题,每小题5分,共25分)
11. 函数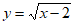 的定义域是____________。
的定义域是____________。
12. 已知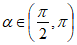 ,且
,且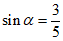 ,则
,则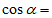 ___________,
___________,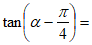 __________。
__________。
13. 已知非零向量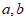 满足
满足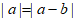 ,则
,则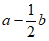 与b的夹角等于__________。
与b的夹角等于__________。
14. 圆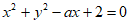 与直线
与直线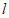 相切于点
相切于点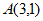 ,则圆的半径为__________,直线
,则圆的半径为__________,直线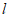 的方程为________________________。
的方程为________________________。
15. 关于x的方程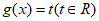 的实根个数记为
的实根个数记为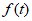 。
。
若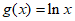 ,则
,则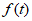 =__________;
=__________;
若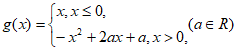 ,存在t使得
,存在t使得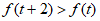 成立,则a的取值范围是________________。
成立,则a的取值范围是________________。
三、解答题(本大题共6小题,共85分)
16. (本小题满分14分)
在△ABC中,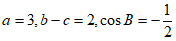 。
。
(Ⅰ)求b,c的值;
(Ⅱ)求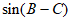 的值。
的值。
17. (本小题满分14分)
已知函数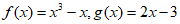 。
。
(Ⅰ)求曲线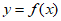 在点
在点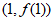 处的切线方程;
处的切线方程;
(Ⅱ)求函数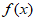 在
在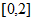 上的最大值;
上的最大值;
(Ⅲ)求证:存在唯一的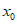 ,使得
,使得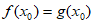 。
。
18. (本小题满分14分)
已知函数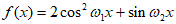 。
。
(Ⅰ)求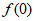 的值;
的值;
(Ⅱ)从①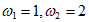 ;②
;②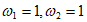 这两个条件中任选一个,作为题目的已知条件,求函数
这两个条件中任选一个,作为题目的已知条件,求函数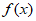 在
在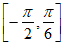 上的最小值,并直接写出函数
上的最小值,并直接写出函数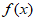 的一个周期。
的一个周期。
19. (本小题满分14分)
已知:函数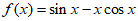 。
。
(Ⅰ)求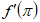 ;
;
(Ⅱ)求证:当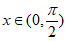 时,
时,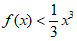 ;
;
(Ⅲ)若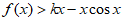 对
对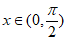 恒成立,求实数k的最大值。
恒成立,求实数k的最大值。
20. (本小题满分14分)
已知O为平面直角坐标系的原点,过点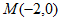 的直线
的直线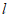 与圆
与圆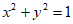 交于
交于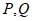 两点。
两点。
(Ⅰ)若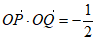 ,求直线
,求直线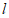 的方程;
的方程;
(Ⅱ)若△OMP与△OPQ的面积相等,求直线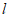 的斜率。
的斜率。
21. (本小题满分15分)
对于集合M,定义函数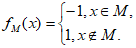 对于两个集合
对于两个集合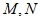 ,定义集合
,定义集合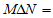
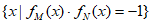 。已知
。已知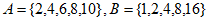 。
。
(Ⅰ)写出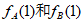 的值,并用列举法写出集合
的值,并用列举法写出集合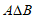 ;
;
(Ⅱ)用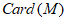 表示有限集合M所含元素的个数,求
表示有限集合M所含元素的个数,求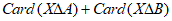 的最小值;
的最小值;
(Ⅲ)有多少个集合对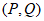 ,满足
,满足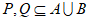 ,且
,且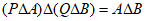 ?
?
【试题答案】
一、选择题:本大题共10小题,每小题4分,共40分,
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | A | D | C | C | D | B | B | D | C |
二、填空题:本大题共5小题,每小题5分,共25分
题号 | 11 | 12 | 13 | 14 | 15 |
答案 |
|
|
|
|
|
三、解答题(本大题共6小题,共85分)
16. 解:(Ⅰ)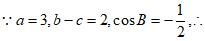 由余弦定理
由余弦定理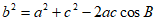 ,
,
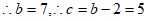 ;
;
(Ⅱ)在△ABC中,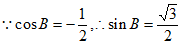 ,由正弦定理有:
,由正弦定理有: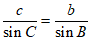 ,
,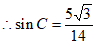 ,
,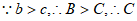 为锐角,
为锐角,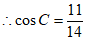 ,
,
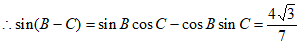 。
。
17. 解:(Ⅰ)由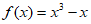 ,得
,得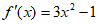 , 1分
, 1分
所以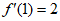 ,又
,又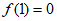 2分
2分
所以曲线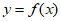 在点
在点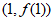 处的切线方程为:
处的切线方程为: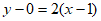 ,
,
即: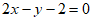 。 3分
。 3分
(Ⅱ)令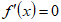 ,得
,得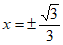 , 4分
, 4分
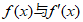 在区间
在区间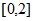 的情况如下:
的情况如下:
x |
|
|
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
6分
因为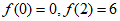 ,
,
所以函数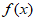 在区间
在区间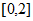 上的最大值为6。 8分
上的最大值为6。 8分
(Ⅲ)证明:设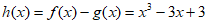 ,
,
则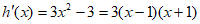 , 9分
, 9分
令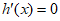 ,得
,得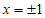 。
。
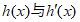 随x的变化情况如下:
随x的变化情况如下:
x |
| -1 |
| 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
则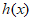 的增区间为
的增区间为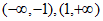 ,减区间为
,减区间为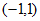 。 11分
。 11分
又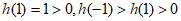 ,所以函数
,所以函数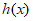 在
在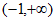 没有零点,
没有零点,
又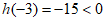 ,
,
所以函数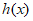 在
在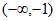 上有唯一零点
上有唯一零点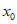 。
。
综上,在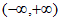 上存在唯一的
上存在唯一的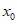 ,使得
,使得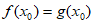 。 14分
。 14分
18. 解:(Ⅰ)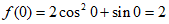 。
。
(Ⅱ)选择条件①,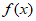 的一个周期为
的一个周期为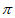 ,
,
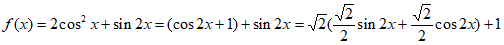 =
=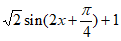 。
。
因为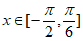 ,所以
,所以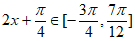 ,所以
,所以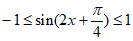 ,所以
,所以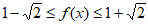 ,
,
当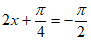 时,即
时,即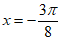 时,
时,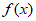 在
在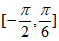 取得最小值
取得最小值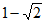 。
。
选择条件②,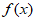 的一个周期为
的一个周期为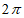 ,
,
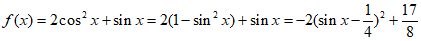 ,
,
因为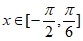 ,所以
,所以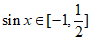 ,
,
所以,当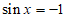 时,即
时,即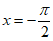 时,
时,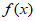 在
在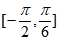 取得最小值-1。
取得最小值-1。
19. 解: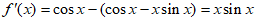 2分
2分
(Ⅰ)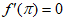 3分
3分
(Ⅱ)令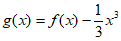 ,则
,则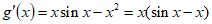 , 5分
, 5分
当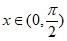 时,设
时,设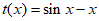 ,则
,则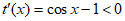
所以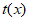 在
在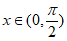 单调递减,
单调递减,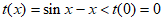
即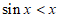 ,所以
,所以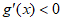 7分
7分
所以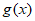 在
在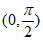 上单调递减,所以
上单调递减,所以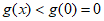 , 8分
, 8分
所以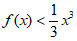 。 9分
。 9分
(Ⅲ)原题等价于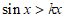 对
对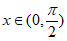 恒成立,
恒成立,
即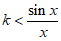 对
对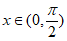 恒成立, 10分
恒成立, 10分
令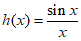 ,则
,则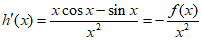 。 12分
。 12分
易知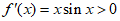 ,即
,即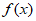 在
在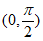 单调递增,
单调递增,
所以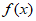
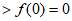 ,所以
,所以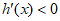 ,
,
故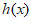 在
在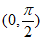 单调递减,所以
单调递减,所以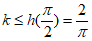 。 14分
。 14分
综上所述,k的最大值为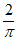 。 15分
。 15分
20. 解:(Ⅰ)依题意,直线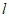 的斜率存在,
的斜率存在,
因为直线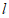 过点
过点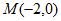 ,可设直线
,可设直线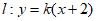 , 1分
, 1分
因为P、Q两点在圆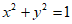 上,所以
上,所以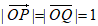 ,
,
因为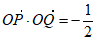 ,所以
,所以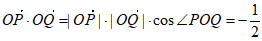 3分
3分
所以∠POQ=120° 所以O到直线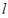 的距离等于
的距离等于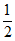 ,
,
所以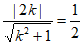 , 4分
, 4分
得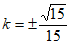 , 5分
, 5分
所以,直线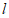 的方程为
的方程为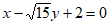 或
或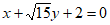 6分
6分
(Ⅱ)(解法一)因为△OMP与△OPQ的面积相等,所以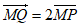 , 8分
, 8分
设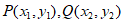 ,所以
,所以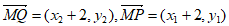 ,
,
所以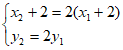 即
即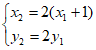 (*); 9分
(*); 9分
因为P,Q两点在圆上,
所以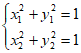 把(*)代入,得
把(*)代入,得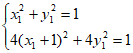 ,
,
所以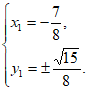 12分
12分
所以,直线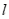 的斜率
的斜率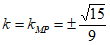 ,即
,即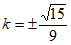 。 13分
。 13分
(解法二)因为△OMP与△OPQ的面积相等,所以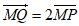 , 8分
, 8分
设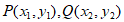 ,所以
,所以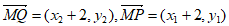 ,
,
所以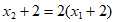 ,即
,即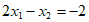 ①;
①;
联立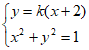 消去y得
消去y得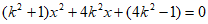 , 9分
, 9分
由韦达定理知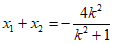 ②
② 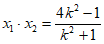 ③
③
由①②可知,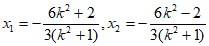 , 12分
, 12分
带入③得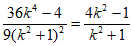 ,所以
,所以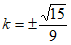 。 14分
。 14分
21. 解:(Ⅰ)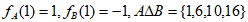 。 3分
。 3分
(Ⅱ)根据题意可知:对于集合C,X,①若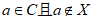 ,则
,则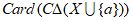 =
=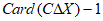 :
:
②若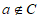 且
且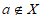 ,则
,则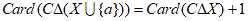 ,
,
所以,要使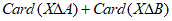 的值最小,
的值最小,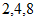 一定属于集合
一定属于集合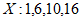 是否属于X不影响
是否属于X不影响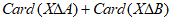 的值;集合X不能含有
的值;集合X不能含有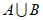 之外的元素。
之外的元素。
所以,当X为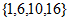 的子集
的子集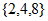 的并集时,
的并集时,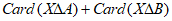 取到最小值4。 8分
取到最小值4。 8分
(Ⅲ)因为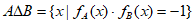 ,
,
所以 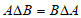 ,
,
由定义可知: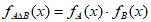 ,
,
所以,对任意元素x,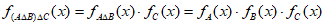 ,
,
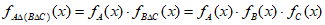 。
。
所以 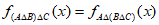 ,
,
所以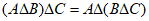 ,
,
由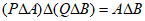 知:
知: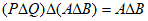 ,
,
所以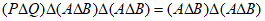 ,
,
所以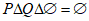 。
。
所以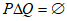 ,即
,即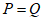 。
。
因为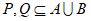 ,
,
所以,满足题意的集合对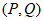 的个数为
的个数为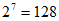 。 14分
。 14分