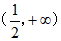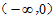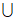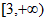(试卷满分140分 考试时间120分钟)
I卷 (满分90分)
一、选择题(本大题共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项。)
1. 已知全集为U,集合A={1,2,3,4,5},B={-3,2},则图中阴影部分表示的集合为
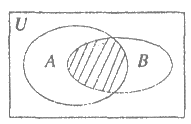
A. {3) B. {-3,2} C. {2} D. {-2,3}
2. 不等式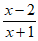 ≤0的解集是
≤0的解集是
A. (-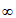 ,-1)
,-1)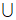 (-1,2] B. [-1,2]
(-1,2] B. [-1,2]
C. (- ,-1)
,-1)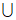 [2,+
[2,+ ) D. (-1,2]
) D. (-1,2]
3. 下列函数中,在区间(0,+ )上为减函数的是
)上为减函数的是
A. 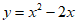 B.
B.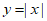
C. 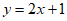 D.
D.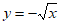
4. 已知函数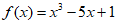 ,则下列区间中一定包含
,则下列区间中一定包含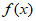 零点的区间是
零点的区间是
A. (-2,-1) B. (-1,0)
C. (0,1) D. (1,2)
5. 若函数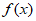 是偶函数,且在区间[0,3]上单调递减,则
是偶函数,且在区间[0,3]上单调递减,则
A. 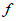 (-1)>
(-1)>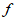 (2)>
(2)>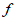 (3) B.
(3) B. 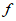 (3)>
(3)> 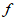 (-1)>
(-1)> 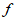 (2)
(2)
C. 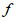 (2)>
(2)>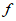 (-1)>
(-1)>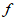 (3) D.
(3) D. 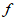 (3)>
(3)>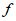 (2)>
(2)>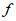 (-1)
(-1)
6. 已知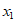 ,
,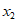 是方程
是方程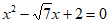 的两根,则
的两根,则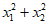 =
=
A. 2 B. 3 C. 4 D. 5
7. 设a,b∈R,且a>b,则下列结论中正确的是
A. 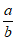 >l B.
>l B. 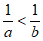 C. |a|>|b| D. a3>b3
C. |a|>|b| D. a3>b3
8. “a=2″是”函数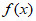 =|x–a|在区间[2,+
=|x–a|在区间[2,+ )上为增函数”的
)上为增函数”的
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
9. 向某容器中匀速注水时容器水面高度h随时间t变化的函数h=f(t)的图像如下图所示,则容器的形状可以是
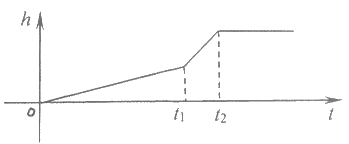
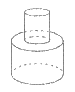
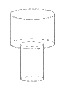
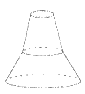
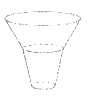
A B C D
10. 若一系列函数的解析式相同、值域相同,但定义域不同,则称这些函数为”同族函数”。函数解析式为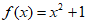 ,值域为{1,3}的同族函数有
,值域为{1,3}的同族函数有
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共5小题,每小题5分,共25分。)
11. 设全集U=R,集合A={x|x<2},集合B={x|x<1},则集合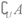 =___________,集合(
=___________,集合(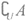 )
)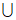 B=____________。
B=____________。
12. 命题”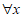 <1,
<1,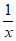 >1″的否定是___________。
>1″的否定是___________。
13. 某班共38人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,16人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为________。
14. 函数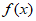 =x+
=x+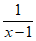 (x>1)的最小值是_______,此时x=_______。
(x>1)的最小值是_______,此时x=_______。
15. 能够说明”设a,b,c是任意实数。若a>b>c,则a+b>c“是假命题的一组整数a,b,c的值依次为__________。
三、解答题(本大题共3小题,共25分。)
16. (本小题8分)
已知a>0,记关于x的不等式(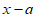 )(
)(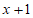 )<0的解集为P,不等式
)<0的解集为P,不等式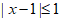 的解集为Q。
的解集为Q。
(I)若a=3,求集合P;
(II)若Q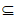 P,求a的取值范围。
P,求a的取值范围。
17. (本小题9分)
已知定义在R上的奇函数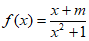 ,m∈R。
,m∈R。
(I)求m;
(II)用定义证明: 在区间[1,+
在区间[1,+ )上单调递减;
)上单调递减;
(III)若实数a满足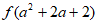 <
<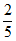 ,求a的取值范围。
,求a的取值范围。
18. (本小题8分)
二次函数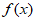 满足
满足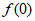 =1,再从条件①和条件②两个条件中选择一个作为已知,求:
=1,再从条件①和条件②两个条件中选择一个作为已知,求:
(I)求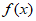 的解析式;
的解析式;
(II)在区间[-1,1]上,函数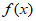 的图像总在一次函数y=2x+m图像的上方,试确定实数m的取值范围。
的图像总在一次函数y=2x+m图像的上方,试确定实数m的取值范围。
条件①:f(x+1)-f(x)=2x;
条件②:不等式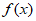 <x+4的解集为(-1,3)。
<x+4的解集为(-1,3)。
注:如果选择条件①和条件②分别解答,按第一个解答计分。
II卷 (满分50分)
一、选择题(本大题共3小题,每小题4分,共1 2分,在每小题列出的四个选项中,选出符合题目要求的一项。)
1. 已知非零实数a,b,c满足:a>b>c,下列不等式中一定成立的有
①ab>bc; ②ac2≥bc2; ③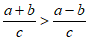 。
。
A. 0个 B. 1个 C. 2个 D. 3个
2. 已知a,b∈R,则”a+b=0″是”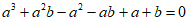 “的
“的
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 (D)既不充分也不必要条件
3. 已知min{a,b)=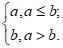 设
设 =min{-x+6,-2x2+4x+6},则函数
=min{-x+6,-2x2+4x+6},则函数 的最大值是
的最大值是
A. 8 B. 7 C. 6 D. 5
二、填空题(本大题共3小题,每小题5分,共15分。)
4. 若函数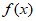 =
=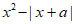 为偶函数,则实数a=_________,函数
为偶函数,则实数a=_________,函数 的单调递增区间是_________。
的单调递增区间是_________。
5. 某学校运动会上,6名选手参加100米决赛。观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1、2、6道选手中的一位获得第一名;观众丁猜测:4、5、6道的选手都不可能得第一名。比赛后发现并没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,则此人是__________。
6. 已知关于x的不等式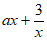 ≤2a在区间(0,+
≤2a在区间(0,+ )上有解,则实数a的取值范围是________。
)上有解,则实数a的取值范围是________。
三、解答题(本大题共2小题,共23分。)
7. (本小题10分)
区间[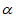 ,
,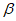 ]的长度定义为
]的长度定义为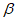 –
–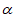 。函数
。函数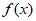 =(1+a2)x2–ax,其中a>0,区间I={x|
=(1+a2)x2–ax,其中a>0,区间I={x|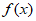 ≤0}。
≤0}。
(I)求I的长度;
(II)求I的长度的最大值。
8. (本小题13分)
若函数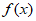 的定义域为D,集合M
的定义域为D,集合M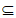 D,若存在非零实数t使得任意x∈M都有x+t∈D,且
D,若存在非零实数t使得任意x∈M都有x+t∈D,且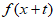 >
>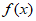 ,则称
,则称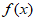 为M上的t-增长函数。
为M上的t-增长函数。
(I)已知函数g(x)=x,函数h(x)=x2,判断g(x)和h(x)是否为区间[-1,0]上的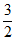 -增长函数,并说明理由;
-增长函数,并说明理由;
(II)已知函数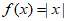 ,且
,且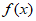 是区间[-4,-2]上的n-增长函数,求正整数n的最小值;
是区间[-4,-2]上的n-增长函数,求正整数n的最小值;
(III)请在以下两个问题中任选一个作答:(如果两问都做,按(i)得分计入总分)
(i)如果对任意正有理数q,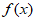 都是R上的q-增长函数,判断
都是R上的q-增长函数,判断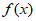 是否一定为R上的单调递增函数,并说明理由;
是否一定为R上的单调递增函数,并说明理由;
(ii)如果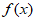 是定义域为R的奇函数,当x≥0时,
是定义域为R的奇函数,当x≥0时,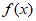 =
=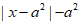 ,且
,且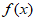 为R上的4-增长函数,求实数a的取值范围。
为R上的4-增长函数,求实数a的取值范围。
参考答案
I卷
一、选择题
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | D | D | C | A | B | D | A | A | C |
二、填空题
11. [2,+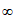 );(-
);(- ,1)
,1) [2,+
[2,+ )
)
12. 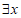 <1,
<1,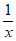 ≤1。
≤1。
13. 12
14. 3;2
15. -1,-2,-3(答案不唯一)
三、解答题
16. 解:(I)由(x-3)(x+1)<0,得P={x|-1<x<3}。
(II)Q={x||x-1|≤1}={x|0≤x≤2}。
由a>0,得P={x|-1<x<a},又Q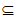 P,所以a>2,即a的取值范围是(2,+
P,所以a>2,即a的取值范围是(2,+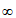 )。
)。
17. 解答:(1)根据 =0得m=0;
=0得m=0;
(2)证明:任取x2> x1≥1,有
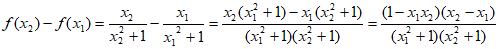 ,
,
因x2> x1>1,故x1x2>1,x2– x1>0,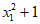 >0,
>0,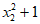 >0,从而
>0,从而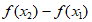 <0,
<0,
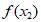 <
<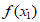 。故
。故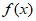 在(1,+
在(1,+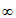 )单调递减。
)单调递减。
(3)因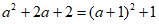 ≥1. 又f(2)=
≥1. 又f(2)=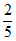 ,结合
,结合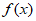 在(1,+
在(1,+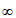 )单调递减,从而
)单调递减,从而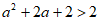 ,a∈(-
,a∈(-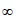 ,-2)
,-2)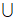 (0,+
(0,+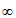 )。
)。
18. 解(1)由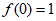 ,可设
,可设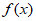 =
=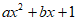 (a≠0)。
(a≠0)。
选择①,则有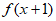
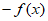 =
=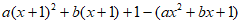 =2ax+a+b,
=2ax+a+b,
由题意,得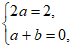 解得
解得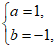 故
故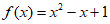 。
。
选择②,则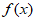 <x+4可化为
<x+4可化为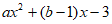 <0。
<0。
由题,方程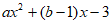 =0的两实根分别为-1和3,
=0的两实根分别为-1和3,
所以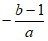 =-1+3=2即2a+b=1,及
=-1+3=2即2a+b=1,及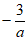 =-1×3=-3即a=1,所以b=-1。
=-1×3=-3即a=1,所以b=-1。
故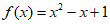 。
。
(2)由题意,得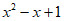 >2x+m,即
>2x+m,即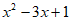 >m,对x∈[-1,1]恒成立。
>m,对x∈[-1,1]恒成立。
令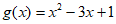 ,则问题可转化为
,则问题可转化为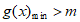 ,
,
又因为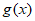 在[-1,1]上递减,所以
在[-1,1]上递减,所以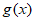 min=g(1)=-1,故m<-1。
min=g(1)=-1,故m<-1。
II卷
题号 | 1 | 2 | 3 | 4 | 5 | 6 |
答案 | B | C | C | 0, | 丁 |
|
7. 解:(1)令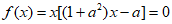 ,解得:
,解得: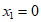 ,
,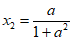 >0,∴
>0,∴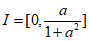 ,
,
(2)∴I的长度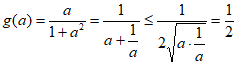 ,当且仅当
,当且仅当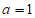 时等号成立。
时等号成立。
∴当a=1时,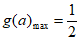 。
。
8. 解:(I)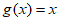 是;因为
是;因为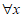 ∈[-1,0],g(x+
∈[-1,0],g(x+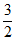 )-
)-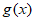 =
=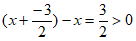 ;
;
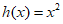 不是,反例:当x=-1时,
不是,反例:当x=-1时,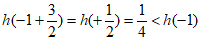 。
。
(II)由题意得,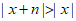 对x∈[-4;-2]恒成立。
对x∈[-4;-2]恒成立。
等价于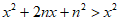 ,即2nx+n2>0对x∈[-4,-2]恒成立
,即2nx+n2>0对x∈[-4,-2]恒成立
因为n>0,所以2nx+n2是关于x的一次函数且单调递增,于是只需-8n+n2>0,
解得n>8,所以满足题意的最小正整数n为9。
(III)(i)不是
构造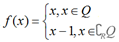 ,则对任意正有理数q,
,则对任意正有理数q,
若x∈Q,则x+q∈Q,因此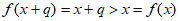 ;
;
若x∈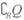 ,则x+q∈
,则x+q∈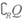 ,因此
,因此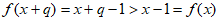 。
。
因此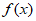 是R上的q-增长函数,但
是R上的q-增长函数,但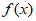 不是增函数。
不是增函数。
(ii)由题意知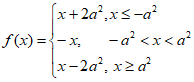
已知任意x∈R,f(x+4)≥f(x),
因为f(x)在[-a2,a2]上递减,所以x, x+4不能同时在区间[-a2,a2]上,
因此4> a2-(- a2)=2 a2
注意到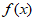 在[-2 a2,0]上非负,在[0,2 a2]上非正
在[-2 a2,0]上非负,在[0,2 a2]上非正
若2 a2<4≤4 a2,当x=-2 a2时,x+4∈[0,2 a2],此时f(x+4)≤f(x),矛盾
因此4>4 a2,即a∈(-1,1)。
当4>4 a2时,下证f(x)为R上的4-增长函数:
①当x+4≤- a2,f(x+4)>f(x)显然成立
②当- a2<x+4<a2时,x< a2-4<-3 a2,此时f(x+4)=-(x+4)>- a2,
f(x)=x+2 a2<- a2,f(x+4)>f(x)
③当x+4≥a2时,f(x+4)=x+4-2 a2>x+2 a2≥f(x)
因此f(x)为R上的4-增长函数
综上,为使得f(x)为R上的4-增长函数a的取值范围是(-1,1)。

 ,
,