本试卷共三道大题,28道小题。满分100分,考试时间120分钟。
一、选择题(本题共16分,每小题2分)
下面各题均有四个选项,符合题意的选项只有一个.
1.2019年5月7日,我国自主创新研发的”东方红3号科学考察船”通过挪威DNV-GL船级社权威认证,成为全球最大静音科考船.”东方红3″是一艘5000吨级深远海科考船,具有全球无限航区航行能力,可持续航行15000海里.将15000用科学记数法表示应为
A.0.15×105 B.1.5×104 C.15×104 D.15×103
2.下列图形中,既是轴对称图形,又是中心对称图形的是
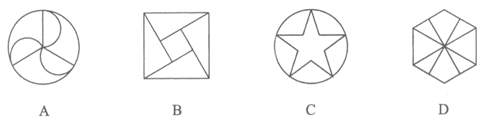
3.实数a,b,c在数轴上的对应点的位置如图所示,则不正确的结论是
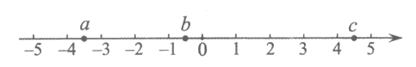
A.|a|>3 B.b-c<0 C.ab<0 D.a>-c
4.如图,AD平分∠BAC,点E在AB上,EF // AC交AD于点G,若∠DGF =40°,则∠BAD的度数为
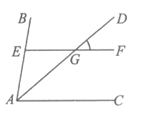
A.20° B.40° C.50° D.80°
5.若一个多边形的内角和为540°,则该多边形的边数是
A.4 B.5 C.6 D.7
6.在下列几何体中,其三视图中没有矩形的是
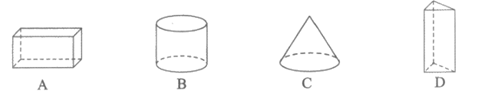
7.如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB = AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为
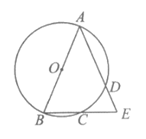
A.0 B.1 C.2 D.3
8.某地区经过三年的新农村建设,年经济收入实现了翻两番(即是原来的22倍).为了更好地了解该地区的经济收入变化情况,统计了该地区新农村建设前后的年经济收入构成结构如下:
建设前年经济收入结构统计图 建设后年经济收入结构统计图
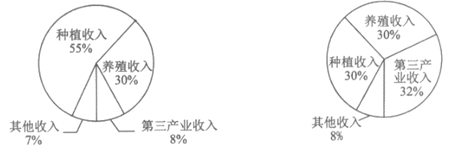
则下列结论中不正确的是
A.新农村建设后,种植收入减少了
B.新农村建设后,养殖收入实现了翻两番
C.新农村建设后,第三产业收入比新农村建设前的年经济收入还多
D.新农村建设后,第三产业收入与养殖收入之和超过了年经济收入的一半
二、填空题(本题共16分,每小题2分)
9.请写出一个比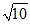 小的整数:_________________.
小的整数:_________________.
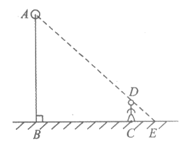
10.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为__________________米.
11.分解因式: xy2-4x=_________________.
12.一个不透明的盒子中装有4个黄球,3个红球和1个绿球,这些球除了颜色外无其他差别.从中随机摸出一个小球,恰好是红球的概率是__________________.
13.如果m+2n=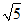 ,那么代数式
,那么代数式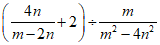 的值为__________________.
的值为__________________.
14.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:”今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:
如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸? (注: 1尺=10寸)
根据题意,该圆的直径为___________________寸.
15.为了做到合理用药,使药物在人体内发挥疗效作用,该药物的血药浓度应介于最低有效浓度与最低中毒浓度之间.某成人患者在单次口服1单位某药后,体内血药浓度及相关信息如下:
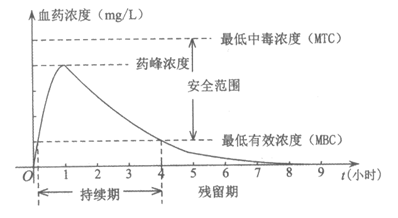
根据图中提供的信息,下列关于成人患者使用该药物的说法中,
①首次服用该药物1单位约10分钟后,药物发挥疗效作用;
②每间隔4小时服用该药物1单位,可以使药物持续发挥治疗作用;
③每次服用该药物1单位,两次服药间隔小于2.5小时,不会发生药物中毒.所有正确的说法是______________.
16.在平面直角坐标系xOy中,函数y1 = x(x <m)的图象与函数y2 =x2 (x≥m)的图象组成图形G.对于任意实数n,过点P(0,n)且与x轴平行的直线总与图形G有公共点.写出一个满足条件的实数m的值为__________(写出一个即可).
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算: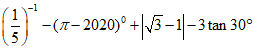 .
.
18.解不等式组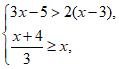 并写出该不等式组的所有非负整数解.
并写出该不等式组的所有非负整数解.
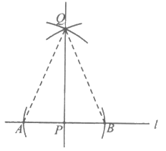
19.下面是小石设计的”过直线上一点作这条直线的垂线”的尺规作图过程.
已知:如图1,直线l及直线l上一点P.
求作:直线PQ,使得PQ⊥l.
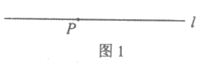
作法:如图2,
①以点P为圆心,任意长为半径作弧,交直线l于点A,B;
②分别以点A,B为圆心,以大于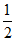 PA的同样长为半径作弧,两弧在直线l上方交于点Q;
PA的同样长为半径作弧,两弧在直线l上方交于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图过程,
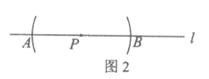
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接QA,QB.
∵QA=(_①___),PA=(_②_),
∴ PQ⊥l(____③____)(填推理的依据).
20.关于x的一元二次方程(m-1)x2-3x+2=0有两个实数根.
(1)求m的取值范围;
(2)若m为正整数,求此时方程的根.
21.如图发,在□ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E .
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
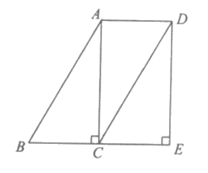
22.如图,在平面直角坐标系xOy中,直线y=x+3与函数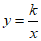 (x>0)的图象交于点A(1,m),与x轴交于点B.
(x>0)的图象交于点A(1,m),与x轴交于点B.
(1)求m,k的值;
(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数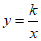 (x>0)的图象于点C,交直线y=x+3于点D.
(x>0)的图象于点C,交直线y=x+3于点D.
①当n=2时,求线段CD的长;
②若CD≥OB,结合函数的图象,直接写出n的取值范围.
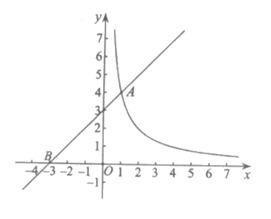
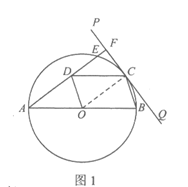
23.如图,AB是⊙O的直径,直线PQ与⊙O相切于点C,以OB,BC为边作□OBCD,连接AD并延长交⊙O于点E,交直线PQ于点F.
(1)求证:AF⊥CF;
(2)连接OC,BD交于点H,若tan∠OCB=3,⊙O的半径是5,求BD的长.
24.北京某超市按月订购一种酸奶,每天的进货量相同.根据往年的销售经验,每天需求量与当天最高气温(单位: °C) 有关.为了确定今年六月份的酸奶订购计划,对前三年六月份的最高气温及该酸奶需求量数据进行了整理、描述和分析,下面给出了部分信息.
a.酸奶每天需求量与当天最高气温关系如下:
最高气温t (单位: °C) | 20≤t<25 | 25≤t<30 | 30≤t≤40 |
酸奶需求量(单位:瓶/天) | 300 | 400 | 600 |
b.2017 年6月最高气温数据的频数分布统计表如下(不完整):
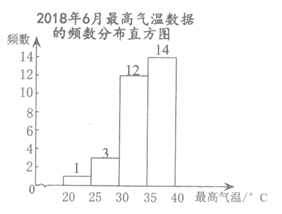
c.2018 年6月最高气温数据的频数分布直方图如下:
2017年6月最高气温数据的频数分布表
分组 | 频数 | 频率 |
20≤t<25 | 3 | |
25≤t<30 | m | 0.20 |
30≤t<35 | 14 | |
35≤t≤40 | 0.23 | |
合计 | 30 | 1.00 |
d.2019年6月最高气温数据如下(未按日期顺序):
25 26 28 29 29 30 31 31 31 32 32 32 32 32 32
33 33 33 33 33 34 34 34 35 35 35 35 36 36 36
根据以上信息,回答下列问题:
(1) m的值为________________;
(2)2019年6月最高气温数据的众数为_________________,中位数为_________________;
(3)估计六月份这种酸奶一天的需求量为600瓶的概率为_________________;
(4)已知该酸奶进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.
①2019年6月这种酸奶每天的进货量为500瓶,则此月这种酸奶的利润为_________________元;
②根据以上信息,预估2020年6月这种酸奶订购的进货量不合理的为
A.550瓶/天 B.600瓶/天 C.380瓶/天
25.如图,C是 上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.
上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.
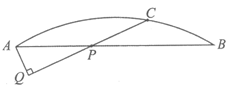
小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ= 0cm)
下面是小石的探究过程,请补充完整:
(1)对于点P在弦AB上的不同位置,画图、测量,得到了线段PC,PA,AQ的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
在PC,PA,AQ的长度这三个量中,确定_____________的长度是自变量,____________的长度和______________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ= PC时,PA的长度约为_______________cm.(结果保留一位小数)
26.在平面直角坐标系xOy中,抛物线y=ax2 +4ax+b (a>0)的顶点A在x轴上,与y轴交于点B.
(1)用含a的代数式表示b;
(2)若∠BAO=45°,求a的值;
(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,结合函数的图象,直接写出a的取值范围.
27.如图,点E是正方形ABCD内一动点,满足∠AEB=90°且∠BAE<45°,过点D作DF⊥BE交BE的延长线于点F .
(1)依题意补全图形;
(2)用等式表示线段EF,DF,BE之间的数量关系,并证明.
(3)连接CE,若AB=2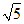 ,请直接写出线段CE长度的最小值.
,请直接写出线段CE长度的最小值.
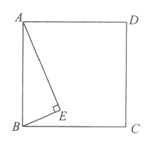
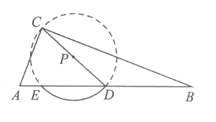
28.在三角开ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E (不与点D重合),那么称弧DE为△ABC的C-中线弧.
例如,如图中弧DE是△ABC的C-中线弧.在平面直角坐标系xOy中,已知△ABC存在C-中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(-3,2),C2(0,2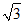 ),C3(2,4),C4(4,2)中,满足条件的点C是_________________;
),C3(2,4),C4(4,2)中,满足条件的点C是_________________;
②若在直线y=kx(k>0)上存在点P是△ABC的C-中线弧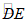 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C -中线弧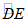 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
参考答案
阅卷须知:
1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可.
2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.
3.评分参考中所注分数,表示考生正确做到此步应得的累加分数.
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | D | C | B | B | C | D | A |
二、填空题(本题共16分,每小题2分)
9.答案不唯一,如: 3 10.9 11.x(y+2)(y-2)
12.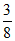 13.2
13.2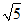 14.26
14.26
15.①② 16.答案不唯一,如:1 (0≤m≤1)
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.解:原式=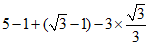 …………………………4分
…………………………4分
=3. …………………………………………………………5分
18.解:原不等式组为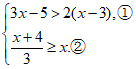 .
.
解不等式①,得x>-1.
解不等式②,得x≤2. ………………………………3分
∴原不等式组的解集为-1<x≤2. …………………………………………4分
∴原不等式组的所有非负整数解为0,1,2. ………………………………5分
19.解:(1)补全的图形如图所示;…………………………2分
(2)①QB;②PB;
③等腰三角形底边上的中线与底边上的高互相重合. ……………………5分
20.解:(1)∵△=(-3)2-4(m-1)×2
=-8m+17. ………………………………1分
依题意,得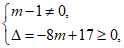
解得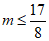 且m≠1. ……………………………………3分
且m≠1. ……………………………………3分
(2)∵m为正整数,
∴ m=2. ………………………………4分
∴原方程为x2-3x+2=0.
解得x1=1,x2=2. ……………………5分
21.(1) 证明:∵四边形ABCD是平行四边形,
∴AD// BC.
∴∠CAD=∠ACB= 90°.
又∵∠ACE=90°,DE⊥BC,
∴四边形ACED是矩形. ………………………………2分
(2)解:∵四边形ACED是矩形,
∴AD=CE=2,AF=EF,AE=CD.
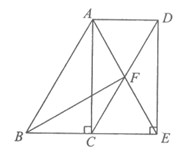
∵四边形ABCD是平行四边形,
∴BC= AD=2,AB=CD.
∴AB= AE.
又∵∠ABC= 60°,
∴△ABE是等边三角形.
∴∠BFE=90°,∠FBE=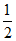 ∠ABE =30°.
∠ABE =30°.
在Rt△BFE中,BF = BE×cos∠FBE=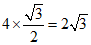 . ………………5分
. ………………5分
22.解: (1) ∵直线y=x+ 3经过点A(1,m),
∴m=4. ……………………………………1分
又∵函数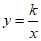 的图象经过点A(1,4),
的图象经过点A(1,4),
∴k=4. ……………………………………2分
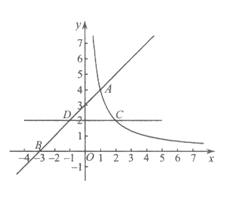
(2)①当n=2时,点P的坐标为(0,2),
∴点C的坐标为(2,2),
点D的坐标为(-1,2).
∴CD=3. ………………………………3分
②0<n≤2或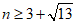 . …………………………5分
. …………………………5分
23.(l)证明:连接OC,如图1.
∵四辺形OBCD是平行四辺形,
∴DC//OB, DC=OB.
∵AO=OB ,
∴DC//AO, DC= AO.
∴四边形OCDA是平行四边形.
∴AF //OC.
∵直线PQ与⊙O相切于点C,OC是半径,
∴∠OCQ= 90°.
∴∠AFC= ∠OCQ= 90°.
即AF⊥CF. ………………………………2分
(2)解:过点B作BN⊥OC于点N,如图2.
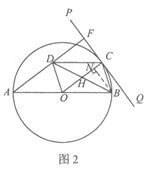
∵四边形OBCD是平行四边形,
∴BD=2BH,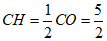
在Rt△BNC中,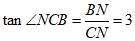
设CN=x,BN=3x,
∴ON=5-x.
在Rt△ONB中,(5-x)2 +(3x)2=52,
解得x1=0 (舍),x2=1.
∴BN=3x=3,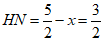 .
.
在Rt△HNB中,由勾股定理可得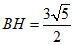 .
.
∴BD=2BH =3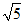 . ………………………………6分
. ………………………………6分
24.解: (1) 6; …………………………1分
(2) 32,32.5 ; ………………………………3分
(3)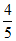 ;…………………………………………4分
;…………………………………………4分
(4)①28000;②C. ……………………………………6分
25.解: (1) PA; PC,AQ; …………………………2分
(2)
…………………………………… 4分
(3) 2.8或6.0. …………………………………… 6分
26.解: (1) ∵y=ax2 +4ax+b
=a(x+2)2 +(b-4a),
∴顶点A的坐标为(-2,b-4a)
∵顶点A在x上,
∴b-4a=0,即b=4a. ……………………………………2分
(2)抛物线为y=ax2 +4ax +4a(a>0),则
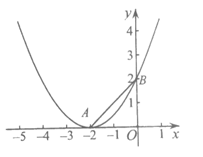
顶点为A(-2,0),
与y轴的交点B(0,4a)在y轴的正半轴.
∵∠BAO=45° ,
∴OB=OA=2.
∴4a=2.
∴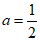 ……………………………………4分
……………………………………4分
(3) 0<a≤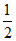 或a=1. ……………………………………6分
或a=1. ……………………………………6分
27.(1)依题意补全图形,如图1..…………………………1分
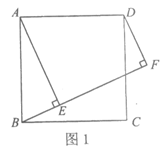
(2)线段EF,DF,BE的数量关系为: EF=DF +BE.……………… 2分
证明:过点A作AM⊥FD交FD的延长线于点M,如图2.……………………3分
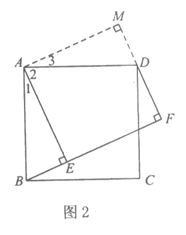
∵∠AEF=∠F=∠M= 90°,
∴四边形AEFM是矩形.
∴∠3+∠2= 90°.
∵四边形ABCD是正方形,
∴∠1+∠2=90°,AB= AD,
∴∠1=∠3.
又∵∠AEB=∠M = 90°,
∴△AEB≌△AMD.……………………………… 5分
∴BE=DM,AE=AM.
∴矩形AEFM是正方形.
∴EF=MF.
∵ MF= DF+ DM,
∴EF=DF+BE. …………………………………………6分
(3)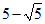 . ……………………………………7分
. ……………………………………7分
28.解: (1) ①C2,C4; ……………………………………2分
②∵△ABC的中线CD=4,B(4,0),k>0,
∴点C在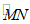 上(点H除外),其中点M(0,
上(点H除外),其中点M(0,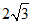 ),点N(4,
),点N(4,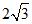 ),点H(2,4).
),点H(2,4).
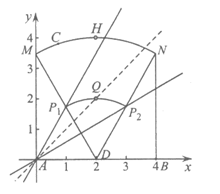
∵点P是△ABC的C-中线弧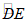 所在圆的圆心,
所在圆的圆心,
∴点P在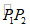 上(点Q除外),其中点P1(1,
上(点Q除外),其中点P1(1,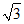 ),点P2(3,
),点P2(3,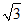 ),点Q(2,2).
),点Q(2,2).
当直线y=kx过点P1(1,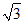 )时,得k=
)时,得k=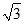 .
.
当直线y=kx过点P2(3,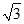 )时,得
)时,得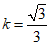 .
.
当直线y=kx过点Q(2,2)时,得k=1.
结合图形,可得k的取值范围是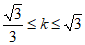 且k≠1.…………………………5分
且k≠1.…………………………5分
(2)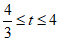 且t≠2.……………………………………7分
且t≠2.……………………………………7分
