本试卷满分100分。考试时长120分钟。
第一部分(选择题 共32分)
一、选择题共8题,每题4分,共32分。在每题列出的四个选项中,选出符合题目要求的一项。
(1)复数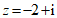 的虚部为
的虚部为
(A)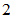
(B)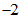
(C)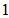
(D)
(2)已知向量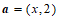 ,
,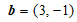 .若
.若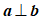 ,则
,则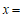
(A)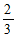 (B)
(B)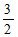 (C)
(C)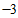 (D)
(D)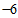
(3)在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为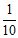 ,那么以下理解正确的是
,那么以下理解正确的是
(A) 某顾客抽奖10次,一定能中奖1次
(B) 某顾客抽奖10次,可能1次也没中奖
(C) 某顾客消费210元,一定不能中奖
(D) 某顾客消费1000元,至少能中奖1次
(4)要得到函数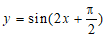 的图象,只要将函数
的图象,只要将函数 的图象
的图象
(A)向右平移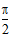 个单位长度 (B)向左平移
个单位长度 (B)向左平移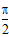 个单位长度
个单位长度
(C)向右平移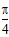 个单位长度 (D)向左平移
个单位长度 (D)向左平移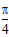 个单位长度
个单位长度
(5)在复平面内,复数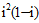 对应的点位于
对应的点位于
(A)第一象限 (B) 第二象限 (C)第三象限 (D) 第四象限
(6)设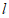 是一条直线,
是一条直线,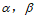 是两个不同的平面,下列命题正确的是
是两个不同的平面,下列命题正确的是
(A)若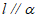 ,
,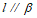 ,则
,则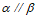
(B)若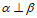 ,
,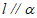 ,则
,则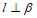
(C)若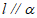 ,
,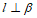 ,则
,则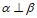
(D)若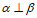 ,
,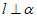 ,则
,则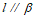
(7) 已知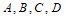 是平面内四个不同的点,则”
是平面内四个不同的点,则”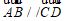 “是”四边形
“是”四边形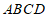 为平行四边形”的
为平行四边形”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
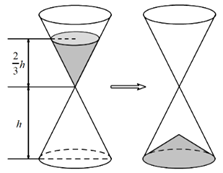
(8)沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,利用细沙全部流到下部容器所需要的时间进行计时.如图,某沙漏由上、下两个圆锥组成,这两个圆锥的底面直径和高分别相等,细沙全部在上部时,其高度为圆锥高度(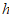 )的
)的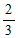 (细管长度忽略不计).假设细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.这个沙堆的高与圆锥的高
(细管长度忽略不计).假设细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.这个沙堆的高与圆锥的高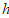 的比值为
的比值为
(A)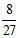
(B)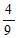
(C)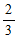
(D)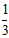
第二部分(非选择题 共68分)
二、填空题共6题,每题3分,共18分。
(9)若函数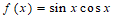 ,则
,则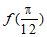 的值为 _________________.
的值为 _________________.
(10)已知复数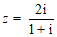 ,则
,则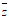 =______ ;
=______ ;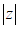 = _________________.
= _________________.
(11)已知在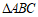 中,
中,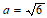 ,
,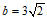 ,
,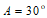 ,则
,则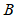 =___________________.
=___________________.
(12)已知甲、乙、丙、丁四人各自独立解决某一问题的概率分别是0.5,0.4,0.3,a,如果甲、乙、丙至少有一人解决该问题的概率不小于丁独立解决这一问题的概率,则a的最大值是_________.
(13)已知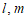 是两条不同的直线,
是两条不同的直线,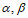 是两个不同的平面,给出下列四个论断:①
是两个不同的平面,给出下列四个论断:①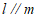 ,②
,②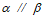 ,③
,③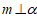 ,④
,④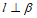 . 以其中的两个论断作为命题的条件,
. 以其中的两个论断作为命题的条件,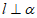 作为命题的结论,写出一个真命题:____________________________________________________.
作为命题的结论,写出一个真命题:____________________________________________________.
(14)在日常生活中,我们会看到如图所示的情境,两个人共提一个行李包.

假设行李包所受重力为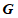 ,作用在行李包上的两个拉力分别为
,作用在行李包上的两个拉力分别为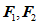 ,且
,且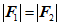 ,
,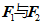 的夹角为
的夹角为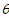 ,给出以下结论:
,给出以下结论:
①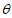 越大越费力,
越大越费力,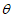 越小越省力;
越小越省力;
②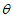 的范围为
的范围为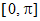 ;
;
③当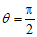 时,
时,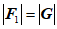 ;
;
④当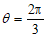 时,
时,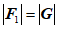 .
.
其中正确结论的序号是________.
注:本题给出的结论中,有多个符合题目要求。全部选对得5分,不选或有错选得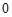 分,其他得3分。
分,其他得3分。
三、解答题共5题,每题10分,共50分。解答应写出文字说明,演算步骤或证明过程。
(15)(本小题10分)
已知函数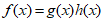 ,其中
,其中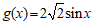 ,
,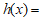 ________.
________.
(Ⅰ)写出函数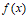 的一个周期(不用说明理由);
的一个周期(不用说明理由);
(Ⅱ)当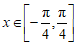 时,求函数
时,求函数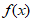 的最大值和最小值.
的最大值和最小值.
从①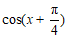 ,②
,②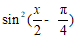 这两个条件中任选一个,补充在上面问题中并作答.
这两个条件中任选一个,补充在上面问题中并作答.
注:如果选择多个条件分别解答,按第一个解答计分。
(16)(本小题10分)
某医院首批援鄂人员中有2名医生,3名护士和1名管理人员.采用抽签的方式,从这六名援鄂人员中随机选取两人在总结表彰大会上发言.
(Ⅰ)写出发言人员所有可能的结果构成的样本空间;
(Ⅱ)求选中1名医生和1名护士发言的概率;
(Ⅲ)求至少选中1名护士发言的概率.
(17)(本小题10分)
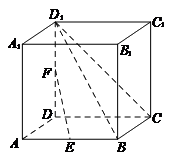
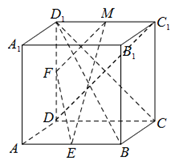
在正方体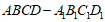 中,
中,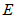 ,
,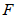 分别为
分别为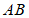 和
和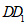 的中点.
的中点.
(Ⅰ)求证: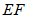 //平面
//平面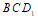 ;
;
(Ⅱ)在棱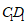 上是否存在一点
上是否存在一点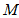 ,使得平面
,使得平面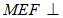 平面
平面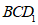 ?
?
若存在,求出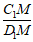 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(18)(本小题10分)
在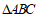 中,
中,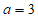 ,
,
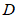 是
是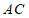 的中点,
的中点,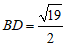 ,
,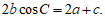
(Ⅰ)求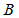 ;
;
(Ⅱ)求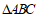 的面积.
的面积.
(19)(本小题10分)
对于任意实数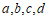 ,表达式
,表达式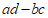 称为二阶行列式(determinant),记作
称为二阶行列式(determinant),记作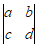 .
.
(Ⅰ)求下列行列式的值:
① 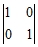 ; ②
; ② 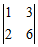 ; ③
; ③ 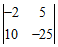 ;
;
(Ⅱ)求证:向量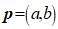 与向量
与向量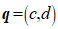 共线的充要条件是
共线的充要条件是 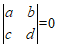 ;
;
(Ⅲ)讨论关于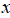 ,
,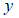 的二元一次方程组
的二元一次方程组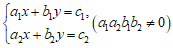 有唯一解的条件,并求出解.
有唯一解的条件,并求出解.
(结果用二阶行列式的记号表示)
【试题答案】
一、选择题(共8题,每题4分,共32分)
(1)C (2)A (3)B (4)D
(5)B (6)C (7)B (8)A
二、填空题(共6题,每题3分,共18分)
(9)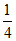 (10)
(10)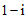
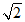
(11)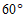 或
或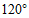 (12)0.79
(12)0.79
(13)若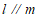 ,
,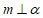 ,则
,则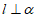 .(答案不唯一) (14)①④
.(答案不唯一) (14)①④
三、解答题(共5题,每题10分,共50分)
(15)(共10分)
解:选择条件①.
(Ⅰ)因为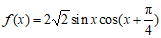

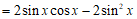
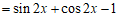
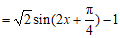 .…………………5分
.…………………5分
所以函数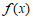 的一个周期为
的一个周期为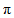 .(答案不唯一)……………7分
.(答案不唯一)……………7分
(Ⅱ)因为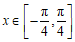 ,所以
,所以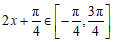 .
.
当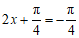 时,即
时,即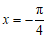 时,函数
时,函数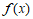 取到最小值
取到最小值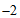 .
.
当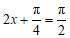 时,即
时,即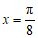 时,函数
时,函数 取到最大值
取到最大值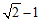 .………10分
.………10分
选择条件②.
(Ⅰ)因为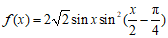
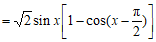
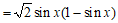
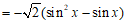 .……………5分
.……………5分
所以函数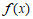 的一个周期为
的一个周期为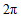 .(答案不唯一)……………7分
.(答案不唯一)……………7分
(Ⅱ)因为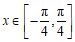 ,所以
,所以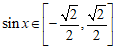 .
.
当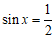 时,即
时,即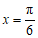 时,函数
时,函数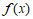 取到最大值
取到最大值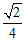 .
.
当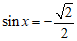 时,即
时,即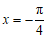 时,函数
时,函数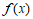 取到最小值
取到最小值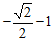 . ……10分
. ……10分
(16)(共10分)
解:(Ⅰ)将2名医生分别记为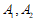 ,3名护士分别记为
,3名护士分别记为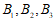 ,1名管理人员记为C. 依题意,样本空间为
,1名管理人员记为C. 依题意,样本空间为
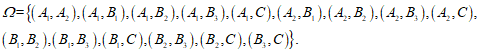
…………………………………………………………………………………4分
(Ⅱ)设事件M为”选中1名医生和1名护士发言”,则
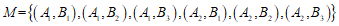 .
.
所以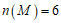 .
.
又因为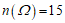 ,
,
所以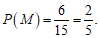 …………………………………………………………7分
…………………………………………………………7分
(Ⅲ)设事件N为”至少选中1名护士发言”,则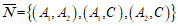 .
.
所以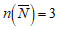 .
.
又因为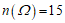 ,
,
所以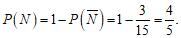 …………………10分
…………………10分
(17)(共10分)
(Ⅰ)证明:取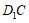 的中点
的中点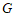 ,连接
,连接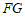 ,
,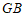 .
.
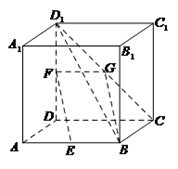
因为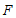 为
为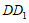 的中点,
的中点,
所以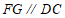 ,且
,且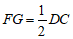 .
.
在正方体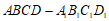 中,
中,
因为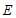 为
为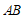 的中点,所以
的中点,所以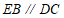 ,且
,且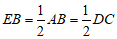 .
.
所以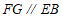 ,且
,且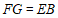 .
.
所以四边形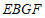 为平行四边形.
为平行四边形.
所以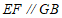 .
.
又因为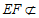 平面
平面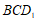 ,
,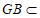 平面
平面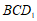 ,
,
所以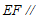 平面
平面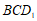 .……………5分
.……………5分
(Ⅱ)解:在棱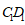 上是否存在一点
上是否存在一点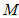 ,使得平面
,使得平面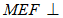 平面
平面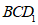 .
.
取点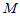 为
为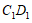 的中点,连接
的中点,连接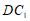 ,
,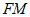 ,
,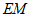 .
.
因为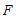 为
为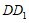 的中点,
的中点,
所以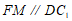 .
.
因为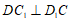 ,所以
,所以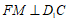 .
.
因为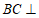 平面
平面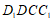 ,
,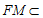 平面
平面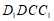 ,
,
所以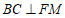 .
.
因为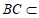 平面
平面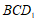 ,
,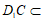 平面
平面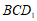 ,
,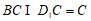 ,
,
所以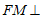 平面
平面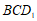 .
.
因为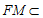 平面
平面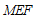 ,
,
所以平面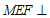 平面
平面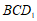 .
.
所以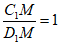 .……………10分
.……………10分
(18)(共10分)
解:(Ⅰ)因为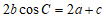 ,
,
由正弦定理可得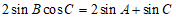 .
.
因为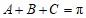 ,所以
,所以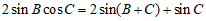 .
.
所以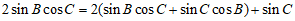 .
.
整理得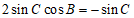 .
.
因为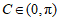 ,所以
,所以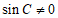 .
.
所以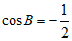 .
.
因为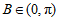 ,所以
,所以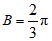 .…………………5分
.…………………5分
(Ⅱ)延长线段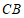 到
到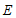 ,使得
,使得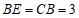 .
.
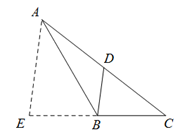
因为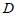 是
是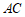 的中点,所以
的中点,所以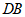 是
是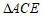 的中位线.
的中位线.
所以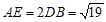 .
.
因为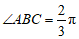 ,所以
,所以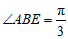 .
.
在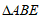 中,由余弦定理
中,由余弦定理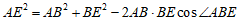 .
.
得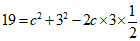 ,整理得
,整理得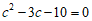 .
.
因为 ,所以
,所以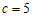 .
.
因此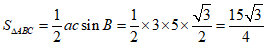 . .…………………10分
. .…………………10分
(19)(共10分)
解:(Ⅰ)①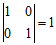 ; ②
; ②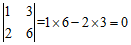 ;③
;③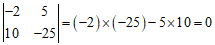 .…………………………3分
.…………………………3分
(Ⅱ)若向量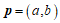 与向量
与向量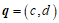 共线,则
共线,则
当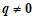 时,有
时,有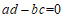 ,即
,即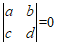 .
.
当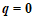 时,有
时,有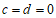 ,即
,即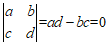 .
.
所以必要性得证.
反之,若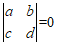 ,即
,即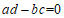 .
.
当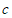 ,
,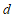 不全为0时,即
不全为0时,即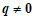 时.
时.
不妨设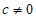 ,则
,则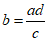 . 所以
. 所以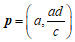 .
.
因为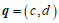 ,所以
,所以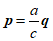 .所以
.所以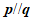 .
.
所以向量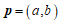 与向量
与向量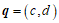 共线.
共线.
当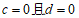 时,
时,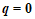 ,所以向量
,所以向量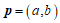 与向量
与向量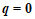 共线.
共线.
充分性得证.
综上,向量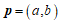 与向量
与向量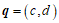 共线的充要条件是
共线的充要条件是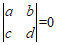 . …………7分
. …………7分
(Ⅲ)用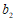 和
和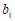 分别乘上面两个方程的两端,然后两个方程相减,消去
分别乘上面两个方程的两端,然后两个方程相减,消去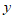 得
得
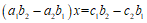 . ①
. ①
同理,消去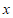 得
得
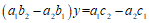 . ②
. ②
所以,当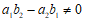 时,即
时,即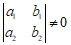 时,由①②可得
时,由①②可得
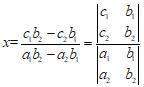 ,
,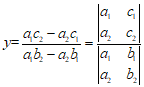 .
.
所以,当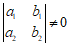 时,方程组
时,方程组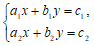 有唯一解且
有唯一解且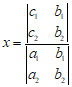 ,
, 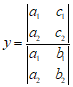 .
.
…………………………………………………………………………………………10分
