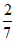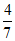(考试时间120分钟 满分150分)
本试卷分为选择题(共40分)和非选择题(共110分)两部分
第一部分(选择题共 40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)在复平面内,复数i(1+i)对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
(2)函数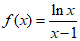 的定义域为
的定义域为
(A)(0,+∞) (B)(0,1)U(1,+∞)
(C)[0,+∞) (D)[0,1)U(1,+∞)
(3)若a,b,c∈R且a>b>c,则下列不等式一定成立的是
( A) ac2>bc2 ( B) a2>b2>c2
( C)a+c>2b (D)a-c>b-c
(4)圆心在直线x-y=0上且与y轴相切于点(0,1)的圆的方程是
(A)(x-1)2+(y-l)2=1 (B)(x+1)2+(y+1)2=1
(C)(x-1)2+(y-1)2=2 (D)(x+1)2+(y+1)2=2
(5)直线l过抛物线y2= 2x的焦点F,且l与该抛物线交于不同的两点A(x1,y1),B(x2,y2).若x1+x2=3,则弦AB的长是
(A)4 (B)5 (C)6 (D)8
(6)设等差数列{an}的公差为d,若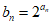 ,则”d<0″是”{bn}为递减数列”的
,则”d<0″是”{bn}为递减数列”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(7)已知函数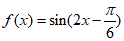 ,则下列四个结论中正确的是
,则下列四个结论中正确的是
(A)函数f(x)的图象关于(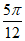 ,0)中心对称
,0)中心对称
(B)函数f(x)的图象关于直线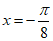 对称
对称
(C)函数f(x)在区间(-π,π)内有4个零点
(D)函数f(x)在区间[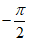 ,0]上单调递增
,0]上单调递增
(8)圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为”表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为”圭”).当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图2是一个根据北京的地理位置设计的圭表的示意图,已知北京冬至正午太阳高度角(即∠ABC)为26.5°,夏至正午太阳高度角(即∠ADC)为73.5°,圭面上冬至线与夏至线之间的距离(即DB的长)为a,则表高(即AC的长)为
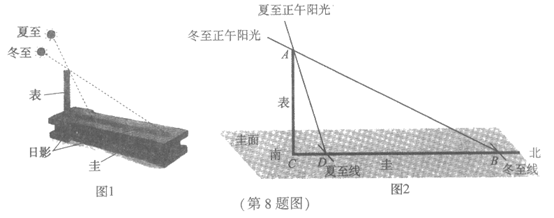
(A)  (B)
(B)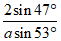
(C) 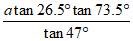 (D)
(D)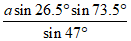
(9)在平行四边形ABCD中,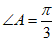 ,AB=2,AD=1,若M,N分别是边BC,CD上的点,且满足
,AB=2,AD=1,若M,N分别是边BC,CD上的点,且满足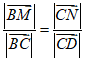 ,则
,则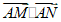 的最大值为
的最大值为
(A)2 (B)4 (C)5 (D)6
(10)设函数f(x)的定义域为D,如果对任意x1∈D,都存在唯一的x2∈D,使得f(x1)+f(x2)=m(m为常数)成立,那么称函数f(x)在D上具有性质Ψm.现有函数:
①f(x)=3x; ②f(x)=3x; ③f(x)= log3x; ④f(x)=tanx.
其中,在其定义域上具有性质Ψm的函数的序号是
(A)①③ (B)①④ (C)②③ (D)②④
第二部分(非选择题 共110分)
二、填空题共5小题,每小题5分,共25分。
(11)已知平面向量a=(m,3),b=(1,6),若a∥b,则m=____________.
(12)在(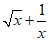 )6的展开式中,常数项为_______________.(用数字作答)
)6的展开式中,常数项为_______________.(用数字作答)
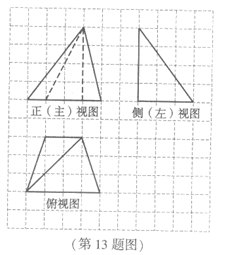
(13)某四棱锥的三视图如图所示,如果网格纸上小正方形的边长为1,那么该四棱锥的体积为________.
(14)已知双曲线C的焦点为F1(0,2),F2(0,-2),实轴长为2,则双曲线C的离心率是________;若点Q是双曲线C的渐近线上一点,且F1Q⊥F2Q,则△QF1F2的面积为___________.
(15)颗粒物过滤效率η是衡量口罩防护效果的一个重要指标,计算公式为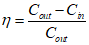 ×100%,其中Cout表示单位体积环境大气中含有的颗粒物数量(单位:ind./L),Cin表示经口罩过滤后,单位体积气体中含有的颗粒物数量(单位:ind./L).某研究小组在相同的条件下,对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试,测试结果如图所示.图中点Aij的横坐标表示第i种口罩第j次测试时Cout的值,纵坐标表示第i种口罩第j次测试时Cin的值(i=1,2,j=1,2,3,4).
×100%,其中Cout表示单位体积环境大气中含有的颗粒物数量(单位:ind./L),Cin表示经口罩过滤后,单位体积气体中含有的颗粒物数量(单位:ind./L).某研究小组在相同的条件下,对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试,测试结果如图所示.图中点Aij的横坐标表示第i种口罩第j次测试时Cout的值,纵坐标表示第i种口罩第j次测试时Cin的值(i=1,2,j=1,2,3,4).
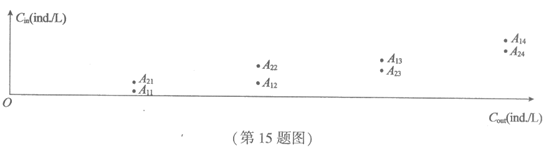
该研究小组得到以下结论:
①在第1种口罩的4次测试中,第4次测试时的颗粒物过滤效率最高;
②在第2种口罩的4次测试中,第3次测试时的颗粒物过滤效率最高;
③在每次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率高;
④在第3次和第4次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率低.
其中,所有正确结论的序号是________________.
注:本题给出的结论中,有多个符合题目要求.全部选对得5分,不选或有错选得0分,其他得3分.
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
(16)(本小题14分)
已知{an}是公差为d的等差数列,其前n项和为Sn,且a5=1,________________.若存在正整数n,使得Sn有最小值.
(I)求{an}的通项公式;
(Ⅱ)求Sn的最小值.
从①a3=-1,②d=2,③d=-2这三个条件中选择符合题意的一个条件,补充在上面问题中并作答.
注:如果选择多个条件分别解答,按第一个解答计分.
(17)(本小题14分)
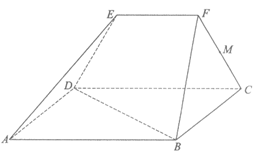
如图,在五面体ABCDEF中,面ABCD是正方形,AD⊥DE,AD=4,DE=EF=2,且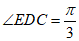 .
.
(I)求证:AD⊥平面CDEF;
(Ⅱ)求直线BD与平面ADE所成角的正弦值;
(Ⅲ)设M是CF的中点,棱AB上是否存在点G,使得MG∥平面ADE?若存在,求线段AG的长;若不存在,说明理由.
(18)(本小题14分)
近年来,随着5G网络、人工智能等技术的发展,无人驾驶技术也日趋成熟.为了尽快在实际生活中应用无人驾驶技术,国内各大汽车研发企业都在积极进行无人驾驶汽车的道路安全行驶测试,某机构调查了部分企业参与测试的若干辆无人驾驶汽车,按照每辆车的行驶里程(单位:万公里)将这些汽车分为4组:[5,6),[6,7),[7,8),[8,9]并整理得到如下的频率分布直方图:
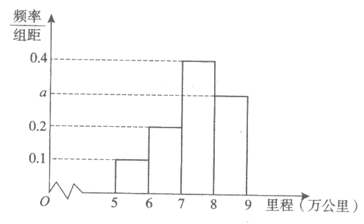
(I)求a的值;
(Ⅱ)该机构用分层抽样的方法,从上述4组无人驾驶汽车中随机抽取了10辆作为样本.从样本中行驶里程不小于7万公里的无人驾驶汽车中随机抽取2辆,其中有X辆汽车行驶里程不小于8万公里,求X的分布列和数学期望;
(Ⅲ)设该机构调查的所有无人驾驶汽车的行驶里程的平均数为μ0.若用分层抽样的方法从上述4组无人驾驶汽车中随机抽取10辆作为样本,其行驶里程的平均数为μ1;若用简单随机抽样的方法从上述无人驾驶汽车中随机抽取10辆作为样本,其行驶里程的平均数为μ2.有同学认为|μ0-μ1|<|μ0-μ2|,你认为正确吗?说明理由.
(19)(本小题14分)
已知椭圆C: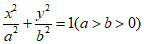 的离心率为
的离心率为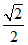 ,且椭圆C经过点(1,
,且椭圆C经过点(1,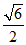 ).
).
(I)求椭圆C的方程;
(Ⅱ)已知过点P(4,0)的直线l与椭圆C交于不同的两点A,B,与直线x=1交于点Q,设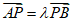 ,
,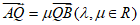 ,求证:λ+μ为定值.
,求证:λ+μ为定值.
(20)(本小题15分)
已知函数f(x)= 2sinx-xcosx-ax(a∈R).
(I)若曲线y=f(x)在点(0,f(0))处的切线的斜率为1.
(i)求a的值;
(ii)证明:函数f(x)在区间(0,π)内有唯一极值点;
(Ⅱ)当a≤1时,证明:对任意x∈(0,π),f(x)>0.
(21)(本小题14分)
设集合A= {a1,a2,a3,a4),其中a1,a2,a3,a4是正整数,记SA= a1+a2 +a3 +a4.对于ai,aj∈A(1≤i<j≤4),若存在整数k,满足k(ai+aj)=SA,则称ai+aj整除SA,设nA是满足ai+aj整除SA的数对(i,j)(i<j)的个数.
(I)若A={1,2,4,8),B={1,5,7,11),写出nA,nB的值;
(Ⅱ)求nA的最大值;
(Ⅲ)设A中最小的元素为a,求使得nA取到最大值时的所有集合A.
参考答案
第一部分(选择题 共40分)
一、选择题(共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项)
(1)B (2)B (3)D (4)A (5)A
(6)C (7)C (8)D (9)C (10)A
第二部分(非选择题 共110分)
二、填空题(共5小题,每小题5分,共25分)
(11) 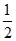 (12)15 (13)12
(12)15 (13)12
(14)2; 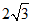 (15)②④
(15)②④
三、解答题(共6小题,共85分。解答应写出文字说明、演算步骤或证明过程)
(16)(本小题14分)
解:(不可以选择③作为补充条件.)
选择①作为补充条件.
解答如下:(I)因为a5 =1,a3 =-1,所以d=1,
所以an=1+(n-5)×1=n-4(n∈N*).…………………………4分
(Ⅱ)由(I)可知a1= -3.
所以 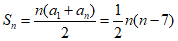 .
.
因为n∈N*.
所以当n=3或4时,Sn取得最小值,最小值为-6.
故存在正整数n=3或4,使得Sn有最小值,最小值为-6.…………14分
选择②作为补充条件.
解答如下:(I)因为a5=1,d=2,
所以an=1+(n-5)×2=2n-9(n∈N*).…………………………4分
(Ⅱ)由(I)可知a1=-7.
所以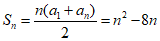 .
.
所以当n=4时,Sn取得最小值,最小值为-16.
故存在正整数n=4,使得Sn有最小值,最小值为-16. ……………………14分
(17)(本小题14分)
解:(I)因为ABCD是正方形,所以AD⊥CD.
又因为AD⊥DE,DE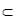 平面CDEF,
平面CDEF,
CD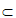 平面CDEF,CD
平面CDEF,CD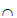 DE=D,
DE=D,
所以AD⊥平面CDEF.………4分
(Ⅱ)由(I)知,AD⊥平面CDEF,
所以平面ABCD⊥平面CDEF.
过点E作EO⊥CD,垂足为O,
则OE⊥平面ABCD.
在平面ABCD内,过O作OH⊥CD,
则OE⊥OH,
如图建立空间直角坐标系O-xyz,
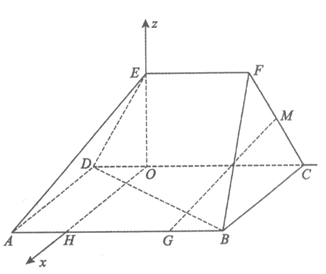
因为AD=4,DE=EF=2,且∠EDC=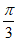 ,所以DO=1 ,OE=
,所以DO=1 ,OE=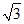 .
.
则A(4,-1,0),B(4,3,0),C(0,3,0),D(0,-1,0),E(0,0,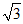 ),
),
所以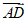 =(-4,0,0),
=(-4,0,0),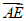 =(-4,1,
=(-4,1,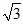 ),
), =(-4,-4,0).
=(-4,-4,0).
设平面ADE的一个法向量为n=(x,y,z),
则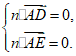 即
即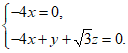
令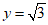 ,则x=0,z=-1,于是n=(0,
,则x=0,z=-1,于是n=(0,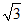 ,-1).
,-1).
设直线BD与平面ADE所成角为θ,
则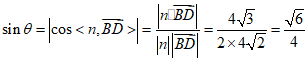 .
.
所以直线BD与平面ADE所成角的正弦值为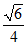 .…………………………10分
.…………………………10分
(Ⅲ)棱AB上存在点G,使得MG∥平面ADE,此时AG=3.理由如下:
因为DC//AB,DC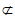 平面ABFE,AB
平面ABFE,AB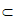 平面ABFE,
平面ABFE,
所以DC//平面ABFE.
因为DC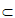 平面DCFE,平面DCFE
平面DCFE,平面DCFE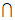 平面ABFE=EF,
平面ABFE=EF,
所以DC//EF.
由(Ⅱ)知,F(0,2,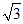 ),M(0,
),M(0,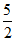 ,
,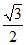 ).
).
设G(4,y,0)(-1≤y1≤3),则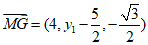 .
.
由(Ⅱ)知,平面ADE的一个法向量为n=(0,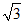 ,-1).
,-1).
若MG∥平面ADE,则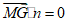 ,即
,即 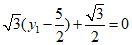 ,解得y1=2,即G(4,2,0).
,解得y1=2,即G(4,2,0).
经验证,此时MG//平面ADE.
所以棱AB上存在点G,使得MG//平面ADE,此时AG=3.……………………14分
(18)(本小题14分)
解:(I)由题意知,1×(0.1+0.2+0.4+a)=1,所以a=0.3.…………………………3分
(Ⅱ)4组无人驾驶汽车的数量比为1:2:4:3,若使用分层抽样抽取10辆汽车,
则行驶里程在[7,8)这一组的无人驾驶汽车有10×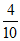 =4辆,
=4辆,
行驶里程在[8,9]这一组的无人驾驶汽车有10×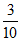 =3辆.
=3辆.
由题意可知,X的所有可能取值为0,1,2.
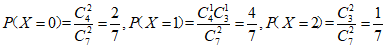 .
.
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
所以X的数学期望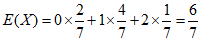 .……………………………11分
.……………………………11分
(Ⅲ)这种说法不正确,理由如下:
由于样本具有随机性,故μ1,μ2是随机变量,受抽样结果影响.
因此有可能μ1更接近μ0,也有可能μ2更接近μ0,
所以|μ0-μ1|<|μ0-μ2|不恒成立.
所以这种说法不正确.……………………………………14分
(19)(本小题14分)
解:(I)由题意可知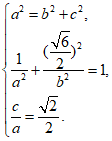 得
得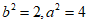 .
.
所以椭圆C得方程为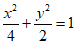 .……………………………………5分
.……………………………………5分
(II)由题意可知,直线l得斜率存在,设直线l的方程为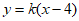 .
.
由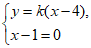 得
得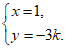 所以
所以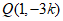 .
.
由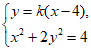 得
得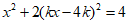 .
.
整理得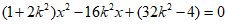 .
.
由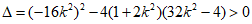 ,得
,得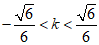 .
.
设直线l与椭圆C的交点A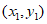 ,B
,B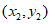 ,
,
则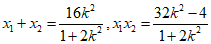 .
.
因为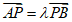 ,
,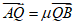 且
且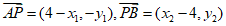 ,
,
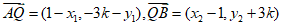 ,
,
所以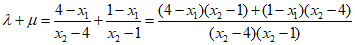
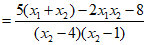 .
.
因为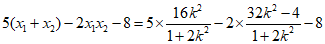
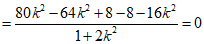 ,
,
所以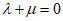 .……………………………………14分
.……………………………………14分
(20)(本小题15分)
解:(I)(i)因为f(x)=2sinx-xcosx-ax,所以f'(x)=2cosx-(cosx-xsinx)-a=cosx+xsinx-a.
因为曲线y=f(x)在点(0,f(0))处的切线的斜率为1,
所以f'(0)=1,即1-a=1,故a=0.
经检验,符合题意.……………………………4分
(ii)由(i)可知f(x)=2sinx-xcosx,f’(x)=cosx+xsinx.
设g(x)=f’(x),则g’(x)=xcosx.
令g’(x)=0,又x∈(0,π),得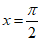 .
.
当x∈(0,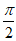 )时,g’(x)>0;当x∈(
)时,g’(x)>0;当x∈(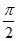 ,π)时,g’(x)<0,
,π)时,g’(x)<0,
所以g(x)在(0,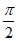 )内单调递增,在(
)内单调递增,在(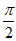 ,π)内单调递减.
,π)内单调递减.
又g(0)=1,g(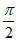 )=
)=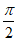 ,g(π)= -1,
,g(π)= -1,
因此,当x∈(0,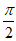 ]时,g(x)>g(0)>0,即f'(x)>0,
]时,g(x)>g(0)>0,即f'(x)>0,
此时f(x)在区间(0,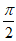 ]上无极值点;
]上无极值点;
当x∈(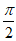 ,π)时,g(x)=0有唯一解x0,即f’(x)=0有唯一解x0,
,π)时,g(x)=0有唯一解x0,即f’(x)=0有唯一解x0,
且易知当x∈(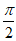 ,x0)时,f’(x)>0,当x∈(x0,π)时,f’(x)<0,
,x0)时,f’(x)>0,当x∈(x0,π)时,f’(x)<0,
故此时f(x)在区间(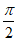 ,π)内有唯一极大值点x0.
,π)内有唯一极大值点x0.
综上可知,函数f(x)在区间(0,π)内有唯一极值点.……………………10分
(Ⅱ)因为f’(x)=cosx+xsinx-a,设h(x)=f’(x),则h’(x)= xcosx.
令h’(x)=0,又x∈(0,π),得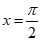 ,
,
且当x∈(0,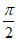 )时,h’(x)>0;当x∈(
)时,h’(x)>0;当x∈(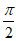 ,π)时,h’(x)<0,
,π)时,h’(x)<0,
所以f’(x)在(0,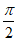 )内单调递增,在(
)内单调递增,在(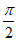 ,π)内单调递减.
,π)内单调递减.
当a≤l时,f'(0)=1-a≥0,f’(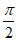 )=
)= 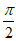 -a>0,,f’(π)=-1-a.
-a>0,,f’(π)=-1-a.
(1)当f'(π)=-1-a ≥0,即a≤-1时,f’(x)≥0.
此时函数f(x)在(0,π)内单调递增,f(x)>f(0)=0;
(2)当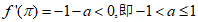 时,因为
时,因为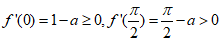 ,所以,在
,所以,在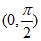 内
内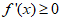 恒成立,而在区间
恒成立,而在区间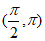 内
内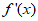 有且只有一个零点,记为
有且只有一个零点,记为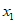 ,
,
则函数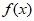 在
在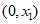 内单调递增,在
内单调递增,在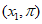 内单调递增。
内单调递增。
又因为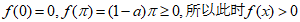 。
。
由(1)(2)可知,当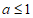 时,对任意
时,对任意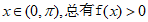 15分
15分
21. (本小题14分)
解:(I)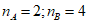 4分
4分
(II)不妨设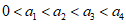
因为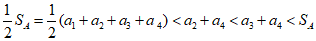 ,所以
,所以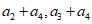 不能整除
不能整除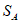 。
。
因为(i,j)最多有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)六种情况,
而(2,4),(3,4)不满足题意,所以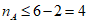
当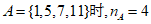 ,所以
,所以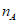 的最大值为4。 9分
的最大值为4。 9分
(III)假设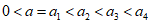
由(II)可知,当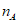 取到最大值4时,
取到最大值4时,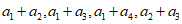 均能整除
均能整除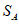
因为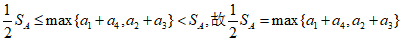 ,
,
所以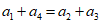
设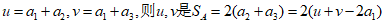 的因数,
的因数,
所以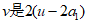 的因数,且u是
的因数,且u是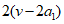 的因数。
的因数。
因为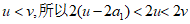
因为v是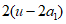 的因数,所以
的因数,所以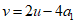 。
。
因为u是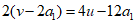 的因数,所以u是
的因数,所以u是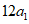 的因数。
的因数。
因为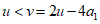 ,所以
,所以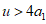 ,所以
,所以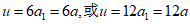 。
。
故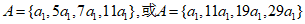 。
。
所以当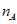 取到最大值4时,
取到最大值4时,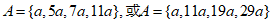 14分
14分