本试卷有三道大题和三道附加题,考试时长120分钟,满分120分。
一、选择题(每小题3分,共30分)
下面各题均有四个选项,其中只有一个是符合题意的.
1、抛物线y=2(x+3)2+5的顶点坐标为( )
A. (3,5) B. (-3,5) C. (-3, -5) D. (3, -5)
2、如果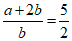 ,那么
,那么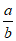 的值是( )
的值是( )
A.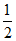 B. 2 C.
B. 2 C.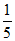 D. 5
D. 5
3、将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
A. y=(x-2)2 B. y=(x-2)2+6 C. y=x2+6 D. y=x2
4、如图,在Rt△ABC,∠C=90°,AC=8,BC=6,则sinB的值等于( )
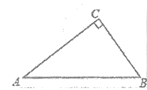
A. 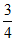 B.
B. 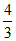 C.
C. 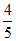 D.
D.
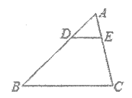
5、如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的周长与△ABC的周长的比等于( )
A. 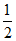 B.
B. 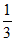 C.
C. 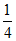 D.
D.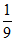
6、如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F、G、H、K四点中的( )
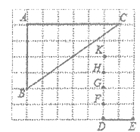
A. F B. G C. H D. K
7、若函数y=x2-4x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<2,则( )
A. y1>y2 B. y1<y2 C. y1=y2 D. y1,y2的大小不确定
8、如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为a,tanα= 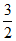 ,则t的值是( )
,则t的值是( )
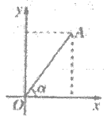
A.1 B. 1. 5 C.2 D. 3
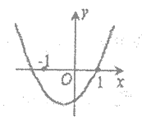
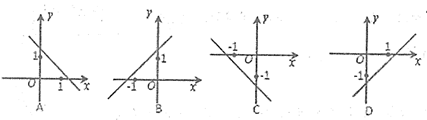
9、已知函数y=(x-a)(x-b)(其中a>b)的图象如下图所示,则函数y=ax+b的图象可能正确的是( )
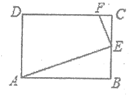
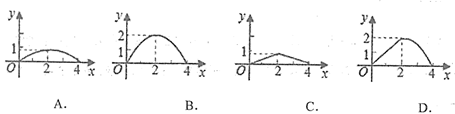
10、如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )
二、填空题(每小题3分,共24分)
11、关于x的方程3x2-4x-k=0有实数根,则k的取值范围是_______________.
12、请写出一个开口向上,且对称轴为直线x=3的二次函数解析式___________.
13、在△ABC中,若sinA= 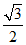 ,tanB=
,tanB= 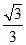 ,则∠C=__________________°.
,则∠C=__________________°.
14、△ABC顶点的坐标分别为A(1,-1),B(4,-1),C(3,-4). 以坐标原点O为位似中心,画出放大的△A1B1C1,使得它与△ABC的位似比等于2:1. 则点C的对应点C1坐标为________________________。
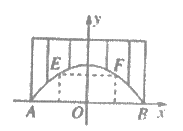
15、廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图。已知抛物线的函数表达式为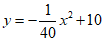 ,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E、F处要安装两盏警示灯,则这两盏灯的水平距离EF是___________________米。
,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E、F处要安装两盏警示灯,则这两盏灯的水平距离EF是___________________米。
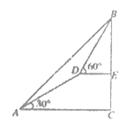
16、一个人由山脚爬到山顶,须先爬倾斜角为30°的山坡300米到达D,再爬倾斜角为60°的山坡200米,这座山的高度为___________________(结果保留根号)
17、已知点A(0,2),B(2,0),点C在y=x2的图象上,若△ABC的面积为2,则这样的C点有____________个。
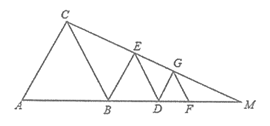
18、如图,在△ACM中,△ABC、△BDE、△DFG是等边三角形,点E、G在△ACM的边CM上,设△ABC、△BDE、△DFG的面积分别为S1、S2、S3,若S1=8,S3=2,则S2=______________。
三、解答题(本题共46分)
19、(4分)计算: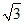 cos30°-
cos30°-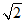 sin 45° – (
sin 45° – (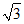 -
-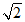 )0
)0
20、(4分)解方程:x2-4x-1=0
21、(6分)二次函数y=-x2+(m-1)x+m的图像与y轴交点坐标是(0,3).
(1)求此二次函数解析式;
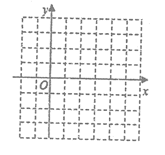
(2)在图中画出二次函数的图像;
(3)当0<x<3时,直接写出y的取值范围。
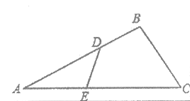
22、(5分)已知:如图,在△ABC中,点D、E分别在边AB,AC上,且∠AED=∠ABC,DE=3,BC=5,AC=12. 求AD的长.
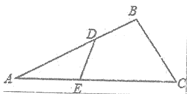
23、(6分)如图,在△ABC中,∠B为锐角,AB=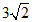 ,AC=5, sinC=
,AC=5, sinC=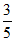 ,求BC的长.
,求BC的长.
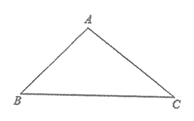
24、(6分)有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | – 24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m=____________;
②若M(-7,- 720),N(n,720)为该函数图象上的两点,则n=_______________;
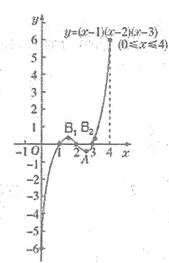
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
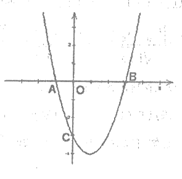
25、(8分)如图,抛物线y=ax2+bx+c与x轴交于点A与点B,与y轴交于点C(0,,-3),且OB=OC=3OA。
(1)求抛物线的解析式;
(2)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形为直角三角形?若存在,求出P点坐标,若不存在,请说明理由;
26、(7分)定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的”等高点”,称此时MP+MQ为PQ的”等高距离”.
(1)若P(1,2),Q(4,2)。
①在点A(1,0),B(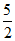 ,4),C(0,3)中,PQ的”等高点”是____________________;
,4),C(0,3)中,PQ的”等高点”是____________________;
②若M(t,0)为PQ的”等高点”,求PQ的”等高距离”的最小值及此时t的值.
(2)若P(0,0),PQ=2,当PQ的”等高点”在y轴正半轴上且”等高距离”最小时,直接写出点Q的坐标.
附加题(共20分)
27、(6分)已知点P (x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式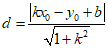 计算.
计算.
例如:求点P(-1,2)到直线y=3x+7的距离:
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(-1,2)到直线y=3x+7的距离为:
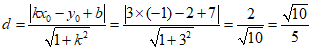
根据以上材料,解答下列问题:
(1)求点P(1,-1)到直线y=x-1的距离;
(2)已知直线y=-2x+4与y=-2x-6平行,求这两条直线之间的距离.
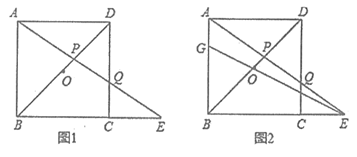
28、(7分)如图1,ABCD是边长为1的正方形,O是对角线BD的中点,Q是边CD上一个动点(点Q不与点C、D重合),直线AQ与BC的延长线交于点E,AE交BD于点P.设DQ=x.
(1)填空:当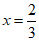 时,CE=_________________;
时,CE=_________________; 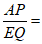 _______________;
_______________;
(2)如图2,直线EO交AB于点G,若BG=y,求y关于x之间的函数关系式;
(3)在第(2)小题的条件下,是否存在点Q,使得PG∥BC?若存在,求x的值;若不存在,说明理由.
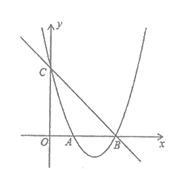
29、(7分)如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.
(1)求这个二次函数的表达式:
(2)将直线BC向下移动n个单位(n>0),若直线与抛物线有交点,求n的取值范围;
(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.
参考答案
一、选择题(每小题3分.共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | A | D | C | B | C | A | C | D | A |
二、填空题(每小题3分,共24分)
11、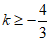 12、y=(x-3)2 (答案不唯一) 13、90 14、(6,-8)或(-6,8)
12、y=(x-3)2 (答案不唯一) 13、90 14、(6,-8)或(-6,8)
15、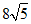 16、150+
16、150+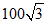 17、4 18、4
17、4 18、4
三、解答题(本题共46分)
19、(4分)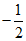
20.(4分)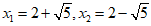
21、(6分)(1)y=-x2+2x+3
(2)如图
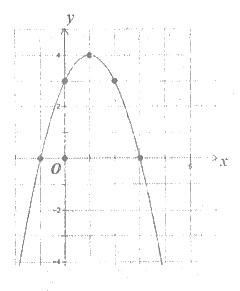
(3) 0<y≤-4
22、(5分)
解:∵∠AED=∠ABC, ∠A=∠A,
∴△AED∽△ABC,
∴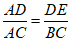
∵DE=3, BC=5, AC=12,
∴ 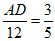 ∴
∴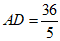
23、(6分)
解:作AD⊥BC于点D, ∴∠ADB=∠ADC=90°.
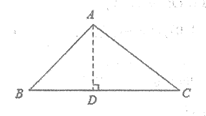
∵AC=5, sinC= 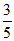 , ∴AD=AC·sinC=3.
, ∴AD=AC·sinC=3.
∴在Rt△ACD中,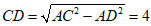 .
.
∵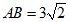 ,
,
∴在Rt△ABD中,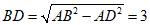 .
.
∴BC=BD+CD=7.
24、(6分)
解:(2)①当x=-2时,y=(x-1)(x-2)(x-3)=-60.
故答案为:-60.
②观察表格中的数据可得出函数图象关于点(2,0)中心对称,
∴-7+n=2×2,解得:n=11.
故答案为:11.
(3)①作点A关于点(2,0)的对称点B1,再在函数图象上找与点B1纵坐标相等的B2点.
②根据表格描点、连线,画出图形如图所示.
25、(8分)
解:(1)抛物线
y=ax2+bx-3与y轴交于点C(0,-3)
∵OB=OC=3OA
∴A(-1,0),B(3,0),代入y=ax2+bx-3,
得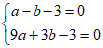
∴y=x2-2x-3.
(II)①当∠P1AC=90°时,可证
△P1AO~△ACO,
∴Rt△P1AO中,tan∠P1AO=tan∠ACO= 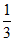 ,
,
∴P1(0,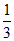 ).
).
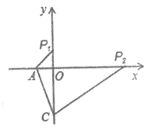
②同理:如图当∠P2CA=90°时,P2(9,0)
③当∠CP3A=90°时,P3(0,0),
综上,坐标轴上存在三个点P,
使得以点P,A,C为顶点的三角形为直角三角形,
分别是P1(0,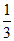 ),P2(9,0),P3(0,0).
),P2(9,0),P3(0,0).
26、(7分)
解:(1)①∵P(1,2),Q(4,2),
∴在点A(1,0),B(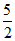 ,4)到PQ的距离为2.
,4)到PQ的距离为2.
∴PQ的”等高点”是A、B,
②如图1,作点P关于x轴的对称点P’,连接P’Q,P’Q与x轴的交点即为”等高点”M,此时”等高距离”最小,最小值为线段P’Q的长,
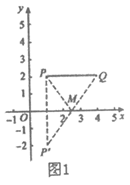
∵P (1,2), ∴P'(1, -2).
设直线P’Q的表达式为y=kx+b,
根据题意,有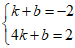 ,解得
,解得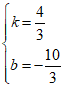
∴直线P’Q的表达式为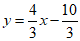 ,
,
当y=0时,解得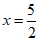 .即
.即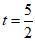 .
.
根据题意,可知PP’=4,PQ=3,PQ⊥PP’,
∴ 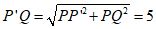 . ∴”等高距离”最小值为5.
. ∴”等高距离”最小值为5.
(2)如图2,过PQ的”等高点”M作MN⊥PQ于点N,
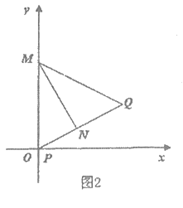
∴PQ=2, MN=2.
设PN=x,则NQ=2-x,
在Rt△MNP和Rt△MNQ中由勾股定理得:
MP2=22+x2=4+x2,MQ2=22+(2-x) 2=x2-4x+8,
∴MP2+MQ2=2x2-4x+12=2 (x-1)2+10,
∵MP2+MQ2≤(MP+MQ)2,
∴当MP2+MQ2最小时MP+MQ也最小,此时x=1,
即PN=NQ,
∴△MPQ为等腰三角形,
∴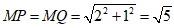 ,
,
如图3,设Q坐标为(x,y),过点Q作QE⊥y轴于点E,
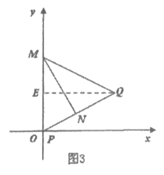
则在Rt△MNP和Rt△MNQ中由勾股定理得:
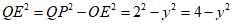 ,
,
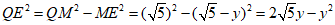
∴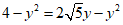 ,解得
,解得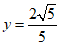 .
.
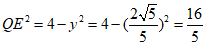 ,
,
当点Q在第一象限时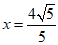 ,当点Q在第二象限时
,当点Q在第二象限时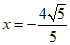 ,
,
∴Q (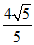 ,
,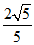 ),或Q (
),或Q (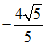 ,
,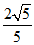 ).
).
附加题
27、(6分)
解:(1)因为直线y=x-1,其中k=1,b=-1,
所以点P(1,-1)到直线y=x-1的距离为:
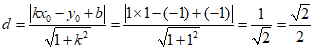 ;
;
(2)当x=0时,y=-2x+4=4,即点(0,4)在直线y=-2x+4,
因为点(0- 4)到直线y=-2x-6的距离为:
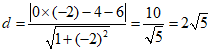
因为直线y=-2x+4与y=-2x-6平行,
所以这两条直线之间的距离为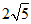 .
.
2.(7分)(1) 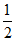 ,
,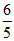 ;
;
(2) 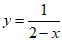
(3)存在;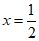 ;
;
3.(7分)(1)这个二次函数的表达式是y=x2-4x+3;
(2) 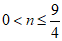 ;
;
(3)当△BMN是等腰三角形时,m的值为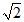 ,
,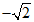 ,1,2.
,1,2.
