本试卷有三道大题,考试时长120分钟,满分150分。
一、选择题(每小题4分,共40分,每题均只有一个正确答案)
1. 已知集合A={-1,0,1),集合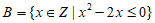 ,那么A∪B=( )
,那么A∪B=( )
A. {-1} B. {0,1} C. {0,1,2} D. {-l,0,1,2}
2. 命题”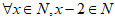 “的否定为( )
“的否定为( )
A. 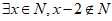 B.
B.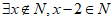
C. 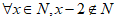 D.
D.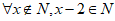
3. 已知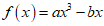 ,若f(1)=3,则f(-1)=( )
,若f(1)=3,则f(-1)=( )
A. -5 B. 5 C. -3 D. 6
4. 若a>0,b>0,且2a+b=4,则ab的最大值为( )
A. 2 B. 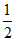 C. 4 D.
C. 4 D.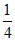
5. 若函数f(x)=(m-l)x+b在R上是增函数,则f(m)与f(l)的大小关系是( )
A. f(m)>f(1) B. f(m)<f(1) C. f(m)=f(1) D. 不确定
6. 若a>b>0,c<d<0,则一定有( )
A. ac< bd B. ac>bd C. ad<bc D. ad> bc
7. 函数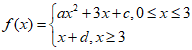 的图像如图所示,则a+b+c+d=( )
的图像如图所示,则a+b+c+d=( )
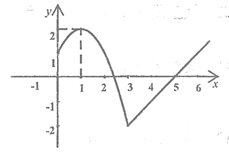
A. -3 B. 3 C. -7 D. 7
8. 已知函数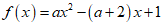 且f(x)在(-2,-1)上恰有一个零点,则a的值可以是( )
且f(x)在(-2,-1)上恰有一个零点,则a的值可以是( )
A. 0 B. -1 C. 2 D. 1
9. “函数f(x)在区间[1,2]上不是增函数”的一个充要条件是( )
A. 存在a∈(1,2),满足f(a)≤f(1)
B. 存在a∈(1,2),满足f(a)≥f(2)
C. 存在a,b∈[1,2],且a<b,满足f(a)=f(b)
D. 存在a,b∈[1,2],且a<b,满足f(a)≥f(b)
10. 某部影片的盈利额(即影片的票房收入与固定成本之差)记为y,观影人数记为x,其函数图像如图(1)所示. 由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后y与x的函数图像.
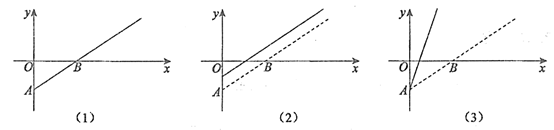
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是( )
A. ①③ B. ①④ C. ②③ D. ②④
二、填空题(每小题5分,共25分)
11. 函数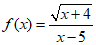 的定义域为___________.
的定义域为___________.
12. 已知函数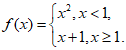 ,则f[f(-1)]=__________;若f(x)=1,则x=______________.
,则f[f(-1)]=__________;若f(x)=1,则x=______________.
13. 已知函数y=f(x)具有以下三条性质:①有最值1;②是偶函数;③在区间(0,+∞)上单调递减,则函数y=f(x)的解析式可以是__________.
14. 关于x的方程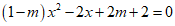 有两个实根,且一个实根小于1,一个实根大于1,则实数m的取值范围是_____________.
有两个实根,且一个实根小于1,一个实根大于1,则实数m的取值范围是_____________.
15. 已知a∈R,函数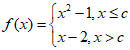 ,当c=1时,不等式f(x)<0的解集是_______________;若函数f(x)恰有2个零点,则c的取值范围是_________________.
,当c=1时,不等式f(x)<0的解集是_______________;若函数f(x)恰有2个零点,则c的取值范围是_________________.
三、解答题(共6小题,共85分. 解答时写出文字说明,演算步骤或证明过程)
16. (本小题14分)设U=R,已知集合A={x||x|<5},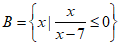 ,求:
,求:
(I) A∩B; (II) 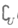 (A∪B); (III) A∪(
(A∪B); (III) A∪(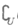 B).
B).
17. (本小题14分)已知函数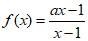 .
.
(I)当a=2,f(x)<1时,求x的取值范围;
(Ⅱ)当f (x)的图像在x轴下方时,求x的取值范围.
18. (本小题14分)已知函数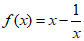 ,
,
(I)函数f(x)是否具有奇偶性?说明理由;
(II)试用函数单调性的定义证明:f(x)在(0,+∞)上为增函数;
(III)若a>0,且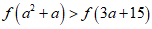 ,求a的取值范围.
,求a的取值范围.
19. (本小题14分)已知函数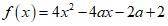
(I)若f(x)在区间[0,2]上不单调,求a的取值范围;
(II)设f(x)在区间[0,2]上的最小值为g(a),求g(a)的解析式及零点.
20. (本小题14分)已知函数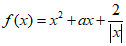 是偶函数.
是偶函数.
(I)求实数a的值;
(II)f(x)是否存在最值?若存在,求出最值,并指出最值点;若不存在,说明理由;
(III)若方程f(x)=b在区间[-1,2]上恰有三个实根,直接写出实数b的取值范围.
21. (本小题15分)设函数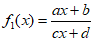 (ad≠bc且abc≠0),
(ad≠bc且abc≠0),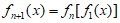 ,n∈N*. 如果对于定义域内的任意x,都有fn(x)=x,则称f1(x)为n阶不动函数.
,n∈N*. 如果对于定义域内的任意x,都有fn(x)=x,则称f1(x)为n阶不动函数.
(I)满足①或②的f1(x)是否为2阶不动函数?直接写出结论:
①a=1,b=2,c=2,d=0;②a=1,b=2,c=-2,d=-1.
(II)当a=1时,若f1(x)为3阶不动函数,试写出满足条件的一组b,c,d的值,并证明你的结论;
(III)当a=1,b=-1,c=1时,
(i)设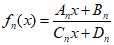 ,如
,如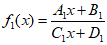 ,…,证明:
,…,证明: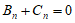 ;
;
(ii)是否存在d使得f1(x)为n阶不动函数?如果存在,写出此时n的取值范围,如不存在,宜接写出你的结论. (不需证明)
参考答案
一、选择题(每小题4分,共40分,每题均只有一个正确答案)
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
D | A | C | A | A | A | A | B | D | C |
二、填空题(每小题5分,共25分)
11. [-4,5)∪(5,+∞) 12. 2 -1
13. y=-x2+1 不唯一 14. (-∞,-1)∪(1,+∞)
15. (-1,1)∪(1,2) [-1,1)∪[2,+∞)
三、解答题(共5小题,共85分. 解答时写出文字说明,演算步骤或证明过程)
16. (本小题14分)
解:A={x|-5<x<5),B={x|0≤x<7).
(1)A∩B=[0,5);
(2)A∪B=(-5,7),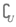 (A∪B)=(-∞,-5]∪[7,+∞);
(A∪B)=(-∞,-5]∪[7,+∞);
(3) 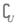 B=(-∞,0)∪[7,+∞),A∪(
B=(-∞,0)∪[7,+∞),A∪(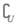 B)= (-∞,5) ∪[7,+∞).
B)= (-∞,5) ∪[7,+∞).
17. (本小题14分)
解:(1)∵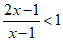
∴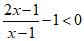
∴0<x<1
∴x的取值范围是(0,1).
(2)∵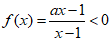
∴(ax-1)(x-1)<0
①a=0时,-(x-1)<0,(1,+∞);
②a>1时,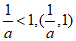 ;
;
③a<0时,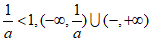 ;
;
④0<a<1时,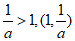 ;
;
⑤a=1时,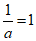 ,
,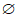 .
.
18. (本小题14分)
解:(I)函数f(x)为奇函数;
(I)定义域为(-∞,0)∪(0,+∞),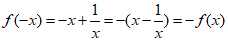
因此f(x)为奇函数.
(II)对于任意的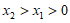
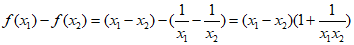
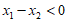 ,
,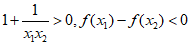 ,所以结论成立.
,所以结论成立.
(III)因为a>0,所以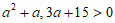 ,均满足定义域要求.
,均满足定义域要求.
根据(II)中结论,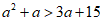 ,解得a>5
,解得a>5
19. (本小题14分)
解:(I)(0,4)
(I)f(x)为二次函数,其对称轴为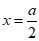
当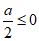 时,f(x)在(0,2)上为增函数,a≤0
时,f(x)在(0,2)上为增函数,a≤0
(II) 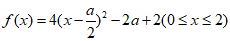 .
.
当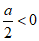 ,即a<0时,f(x)在[0,2]上为增函数,
,即a<0时,f(x)在[0,2]上为增函数,
此时f(x)的最小值为f(0)=-2a +2.
当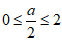 ,即0≤a≤4时,f(x)的最小值为
,即0≤a≤4时,f(x)的最小值为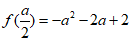 ;
;
当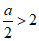 ,即a>4时,f(x)在[0,2]上为减函数,此时f(x)的最小值为f(2)=-10a+18;
,即a>4时,f(x)在[0,2]上为减函数,此时f(x)的最小值为f(2)=-10a+18;
综上所述,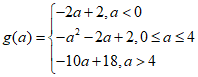
g(a)的零点为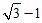
20. (本小题14分)
(1)a=0;
(I)定义域为(-∞,0)∪(0,+∞),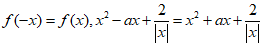
ax=0,对于任意定义域内的x都成立,a=0
(II)首先证明f (x)的单调性
(i)先证明f(x)在(1,+∞)单调递增,对于任意1<x1<x2,
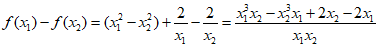
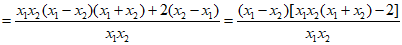 .
.
x1-x2<0,x1x2>0,x1x2 (x1+x2)-2>0,f(x1)<f(x2),结论成立.
(ii)再证明f (x)在(0,1)单调递减,对于任意0<x1<x2<1,
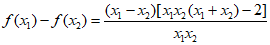
x1-x2<0,x1x2>0,x1x2 (x1+x2)-2<0,f(x1)>f(x2),结论成立。
(iii)由于f(x)为偶函数,因此单调增区间为(1,+∞)和(-1,0)
单调减区间为(-∞,-1)和(0,1)
所以当x=±1时,取得最小值f(±1)=3
(III)b∈(3,5].
21. (本小题15分)
(I)①不是2阶不动函数,②是2阶不动函数
(II)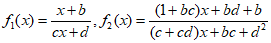
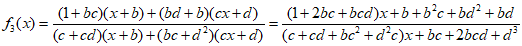
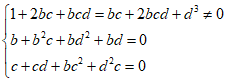
bc=-d2-d-1且d≠-1
满足上式的结果即可
(III)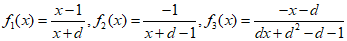
(i)该命题等价于若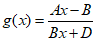 ,其中AD+B2≠0则当
,其中AD+B2≠0则当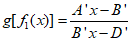 时,有
时,有
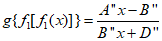
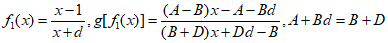
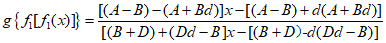
若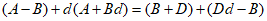
则A+Ad+Bd2=B+D+Dd=A+Bd+Dd
即Ad+Bd2=Bd+Dd 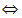 [(A +Bd)- (B+D)]d=0,成立.
[(A +Bd)- (B+D)]d=0,成立.
(ii)结论f1 (x)为n阶不动函数,其中n≥3
