本试卷分两部分,第一部分16道题,第二部分10道题,考试时长90分钟,满分100分。
第—部分:一、选择题(每小题3分,共21分)
1. 一个圆柱的母线长为5,底面半径为2,则圆柱的轴截面的面积是( )
A. 10 B. 20 C. 30 D. 40
2. 若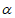 ∥
∥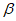 ,a∥
,a∥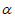 ,则a与
,则a与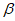 的关系为( )
的关系为( )
A. a∥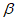 B.
B. 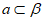 C. a∥
C. a∥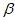 或
或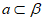 D.
D.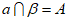
3. 棱长都是1的三棱锥的表面积为( )
A. 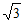 B.
B. 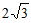 C.
C. 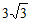 D.
D.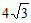
4. 下列条件中,能使直线m⊥平面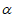 的是( )
的是( )
A. m⊥b,m⊥c,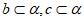 B. m⊥b,b∥
B. m⊥b,b∥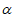
C. 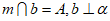 D. m∥b,b⊥
D. m∥b,b⊥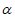
5. 经过平面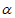 外两点,作与
外两点,作与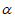 平行的平面,则这样的平面可以作( )
平行的平面,则这样的平面可以作( )
A. 1个或2个 B. 0个或1个 C. 1个 D. 0个
6. 已知长方体一个顶点上三条棱的长分别是3、4、5,且它的顶点都在同一球面上,则这个球的表面积是( )
A. 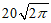 B.
B. 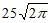 C.
C. 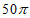 D.
D.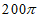
7. 直线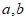 是不同的直线,平面
是不同的直线,平面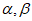 是不同的平面,下列命题正确的是( )
是不同的平面,下列命题正确的是( )
A. 直线a∥平面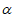 ,直线
,直线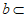 平面
平面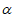 ,则直线a∥直线b
,则直线a∥直线b
B. 直线a∥平面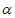 ,直线b∥平面
,直线b∥平面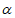 ,则直线a∥直线b
,则直线a∥直线b
C. 直线a∥直线b,直线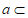 平面
平面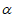 ,直线
,直线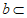 平面
平面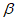 ,则平面a∥
,则平面a∥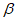
D. 直线a∥直线b,直线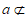 平面
平面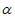 ,直线
,直线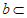 平面
平面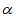 ,则直线a∥平面
,则直线a∥平面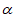
二、填空题(每题4分,共24分)
8. 正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积是__________。
9. 正四棱柱的高为3cm,对角线长为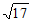 cm,则正四棱柱的侧面积为___________。
cm,则正四棱柱的侧面积为___________。
10. 圆锥的底面半径是3,高是4,则圆锥的侧面积是____________。
11. 在Rt△ABC中,D是斜边AB的中点,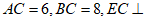 平面ABC,且
平面ABC,且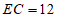 ,则
,则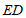 =____________。
=____________。
12. 设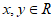 ,复数
,复数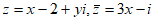 ,
,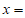 ____________;
____________;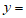 __________。
__________。
13. 正四棱锥底面边为2,高是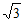 ,则它的全面积为_____________。
,则它的全面积为_____________。
三、解答题(本题共25分)
14. 实数m取何值时,复数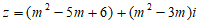 满足下列条件:
满足下列条件:
(1)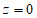 (2)z为虚数 (3)z为纯虚数
(2)z为虚数 (3)z为纯虚数
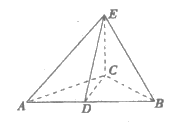
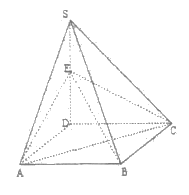
15. 如图,四棱锥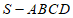 的底面是正方形,SD⊥平面ABCD,E是SD的中点。
的底面是正方形,SD⊥平面ABCD,E是SD的中点。
(1)求证:SB∥平面EAC
(2)求证:AC⊥BE。
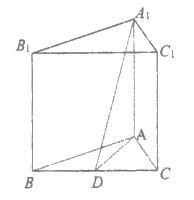
16. 如图,三棱柱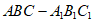 中,
中,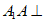 底面,
底面,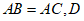 是BC的中点。
是BC的中点。
(Ⅰ)求证:BC⊥平面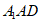 ;
;
(Ⅱ)若∠BAC=90°,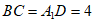 ,求三棱柱
,求三棱柱 的体积。
的体积。
第二部分:SAT数学(选择题:每小题3分,共30分)
1.
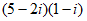
Which of the following is equivalent to the complex number expression above?(Note: 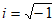 )
)
A. 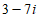 B.
B. 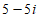 C.
C. 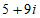 D.
D.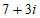
2. Which of the following complex numbers is equivalent to 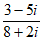 ?(Note:
?(Note: 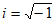 )
)
A. 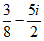 B.
B. 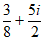 C.
C. 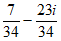 D.
D.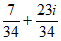
3. If 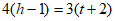 , what is h in terms of t?
, what is h in terms of t?
A. 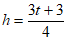 B.
B. 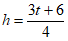 C.
C. 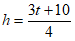 D.
D.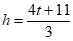
4.
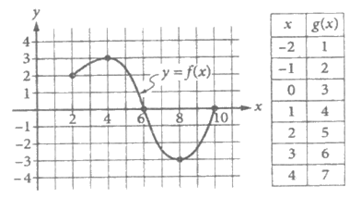
The complete graph of the function f and a table of values for the function g are shown above. The maximum value of f is k. What is the value of g(k)?
A. 7 B. 6 C. 3 D. 0
5. A chef plans to cook a maximum of 100 entrées for a dinner party; each entrée will include either chicken or fish. The cost of ingredients for each chicken entrée is $7, and the cost of ingredients for each fish entrée is $9. If no more than $850 can be spent on ingredients for the entrées and the chef cooks c chicken entrées and f fish entrées, which of the following systems best represents the constraints on c and f?
A. 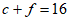 B.
B.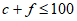
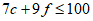
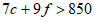
C. 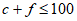 D.
D.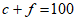
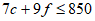
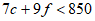
6. Which of the following expressions is equivalent to 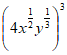 ?
?
A. 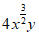 B.
B. 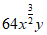 C.
C. 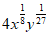 D.
D.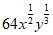
7. Which of the following expressions is equivalent to 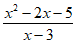 ?
?
A. 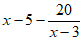 B.
B.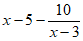
C. 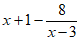 D.
D.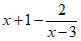
8.
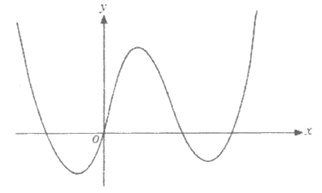
Which of the following could be an equation of the graph above?
A. 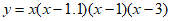
B. 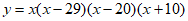
C. 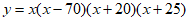
D. 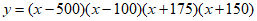
9.
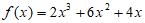
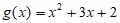
The polynomials f(x) and g(x) are defined above.
Which of the following polynomials is divisible by 2x+3?
A. 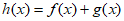 B.
B.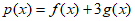
C. 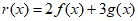 D.
D.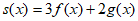
10.
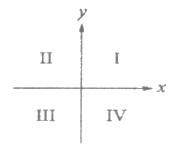
If the system of inequalities 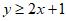 and
and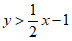 is graphed in the xy-plane above, which quadrant contains no solutions to the system?
is graphed in the xy-plane above, which quadrant contains no solutions to the system?
A. Quadrant II B. Quadrant III
C. Quadrant IV D. There are solutions in all four quadrants.
【试题答案】
第一部分:
一、选择题(每小题3分,本题共21分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
答案 | B | C | A | D | B | C | D |
二、填空题(每小题4分,本题共24分)
8. 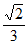 9. 24 10.
9. 24 10. 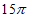 11. 13
11. 13
12. 5 1 13. 12
三、解答题(本题共25分)
14. (1)当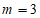 时,
时,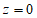
(2)当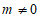 且
且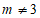 时,z为虚数
时,z为虚数
(3)当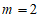 时,z为纯虚数
时,z为纯虚数
15. (1)连BD交AC于O点,连EO
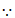 E为SD中点
E为SD中点
O为BD中点
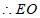 为△SBD中经线
为△SBD中经线
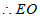 ∥SB
∥SB
又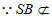 面EAC
面EAC 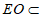 面EAC
面EAC
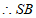 ∥面EAC
∥面EAC
(2)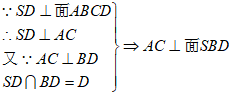
∴AC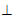 BE
BE
16.
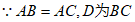 中点
中点
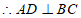
又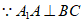
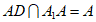
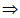 BC
BC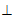 面
面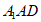
(2)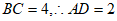
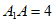 ,
,
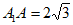
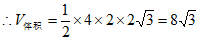
第二部分:SAT数学(共30分)
(选择题,共10小题,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | C | C | B | C | B | D | B | B | C |
