本试卷有两大部分,考试时长90分钟,满分100分。
第一部分:学考数学(50分)
一、选择题:本大题共5小题,每小题4分,共20分。
1. 在数列{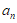 }中,a1=1,an·an-1=2,(n=2,3,…,),那么a8等于( )
}中,a1=1,an·an-1=2,(n=2,3,…,),那么a8等于( )
A. -2 B. -1 C. 1 D. 2
2. 已知数列{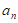 }的前n项和Sn=n2-1,那么a3等于( )
}的前n项和Sn=n2-1,那么a3等于( )
A. 5 B. 6 C. 7 D. 8
3. 在等差数列{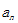 }中,已知a1=2,d=2,则S20=( )
}中,已知a1=2,d=2,则S20=( )
A. 230 B. 420 C. 450 D. 540
4. 等差数列{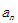 }的前n项和为Sn,若a1=2,S3=12,则a6等于( )
}的前n项和为Sn,若a1=2,S3=12,则a6等于( )
A. 8 B. 10 C. 12 D. 14
5. 在等比数列{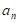 }中,如果a6=6,a9=9,那么a3为( )
}中,如果a6=6,a9=9,那么a3为( )
A. 4 B. 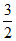 C.
C. 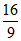 D. 2
D. 2
二、填空题:本大题共4小题,每小题3分,共12分。
6. 已知等差数列{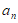 }中,a1=4,S8=172,则a8=________。
}中,a1=4,S8=172,则a8=________。
7. 在等差数列{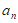 }中,已知a1+ a2=5,a3+ a4=9,那么a5+ a6=________。
}中,已知a1+ a2=5,a3+ a4=9,那么a5+ a6=________。
8. 等比数列{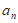 }中,S3=21,2a2= a3,则an=_________。
}中,S3=21,2a2= a3,则an=_________。
9. 在等比数列{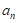 }中,a2=9,a5=243,则数列{
}中,a2=9,a5=243,则数列{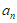 }的前4项和为________。
}的前4项和为________。
三、解答题:共3道大题,共18分,请写出解题步骤。
10. 设等差数列{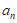 }的前n项和为Sn,a10=30,a20=50,
}的前n项和为Sn,a10=30,a20=50,
(1)求数列{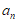 }的通项公式;
}的通项公式;
(2)若Sn=242,求n
11. 已知数列{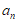 }为等比数列,若a1+ a2+ a3=7,a1 a2 a3=8,求数列{an}的通项公式。
}为等比数列,若a1+ a2+ a3=7,a1 a2 a3=8,求数列{an}的通项公式。
12. 已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4。
(1)求{an}的通项公式;
(2)设Cn=an+bn,求数列{Cn}的前n项和。
第二部分:SAT数学 (50分)
一、选择题:本大题共20小题,每小题2分,共40分。
1. What is the value of(2+8i)(1-4i)-(3-2i)(6+4i)?
(Note:i=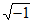 )
)
A. 8 B. 26 C. 34 D. 50
2. 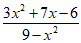
Which of the following is equivalent to the quotient
shown above for x≠-3 and x≠3 ?
A. 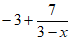 B.
B.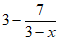
C. 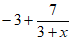 D.
D.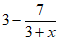
3. Samantha offers two different packages of yoga classes at her yoga studio. She offers two hot yoga sessions and three zero gravity yoga sessions at a total cost of $ 400. She also offers four hot yoga sessions and two zero gravity sessions at a price of $ 440. Samantha wants to offer a larger package for long-time clients in which the cost must exceed $ 800. If Samantha does not wish to include more than 13 sessions for the long-time client package, will she be able to create this package for her clients?
A. No, because the closest package that she can offer consists of three hot yoga and three zero gravity yoga sessions.
B. No, because the closest package that she can offer consists of four hot yoga and four zero gravity yoga sessions.
C. Yes, because she can offer five hot yoga and five zero gravity yoga sessions.
D. Yes, because she can offer six hot yoga and six zero gravity yoga sessions,
4.
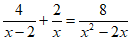
What value of x satisfies the equation above?
A. 0 B. 2 C. 14 D. No value of x satisfies the equation.
5. In order to determine if treatment X is successful in improving eyesight, a research study was conducted. From a large population of people with poor eyesight, 300 participants were selected at random. Half of the participants were randomly assigned to receive treatment X, and the other half did not receive treatment X. The resulting data showed that participants who received treatment X had significantly improved eyesight as compared to those who did not receive treatment X. Based on the design and results of the study, which of the following is an appropriate conclusion?
A. Treatment X is likely to improve the eyesight of people who have poor eyesight.
B. Treatment X improves eyesight better than all other available treatments.
C. Treatment X will improve the eyesight of anyone who takes it.
D. Treatment X will cause a substantial improvement in eyesight.
6. In the xy-plane, the line determined by the points (2, k) and (k, 32) passes through the origin. Which of the following could be the value of k ?
A. 0 B. 4 C. 8 D. 16
7. Graphene, which is used in the manufacture of integrated circuits, is so thin that a sheet weighing one ounce can cover up to 7 football fields. If a football field has an area of approximately 1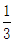 acres, about how many acres could 48 ounces of graphene cover?
acres, about how many acres could 48 ounces of graphene cover?
A. 250 B. 350 C. 450 D. 1,350
8. Of the following four types of savings account plans, which option would yield exponential growth of the money in the account?
A. Each successive year, 2% of the initial savings is added to the value of the account.
B. Each successive year, 1.5% of the initial savings and $100 is added to the value of the account.
C. Each successive year, 1% of the current value is added to the value of the account.
D. Each successive year, $100 is added to the value of the account.
9.
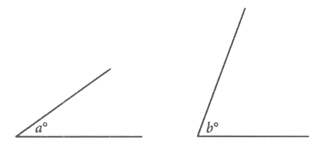
Note: Figures not drawn to scale.
The angles shown above are acute and sin(a︒) = cos(b︒). If a = 4k – 22 and b = 6k – 13, what is the value of k ?
A. 4.5 B. 5.5 C. 12.5 D. 21.5
10. A rectangle was altered by increasing its length by 10 percent and decreasing its width by p percent. If these alterations decreased the area of the rectangle by 12 percent, what is the value of p ?
A. 12 B. 15 C. 20 D. 22
11. In planning maintenance for a city’s infrastructure, a civil engineer estimates that, starting from the present, the population of the city will decrease by 10 percent every 20 years. If the present population of the city is 50,000, which of the following expressions represents the engineer’s estimate of the population of the city t years from now?
A. 50,000(0.1)20 t
B. 50,000(0.1)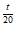
C. 50,000(0.9)20t
D. 50,000(0.9)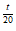
12. If x and y are positive, which of the following is equivalent to 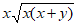 ?
?
A. 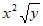 B.
B. 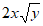 C.
C. 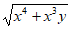 D.
D.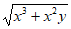
13.
Handedness | ||
Gender | Left | Right |
Female | ||
Male | ||
Total | 18 | 122 |
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth-grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. If there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)
A. 0.410 B. 0.357 C. 0.333 D. 0.250
14.
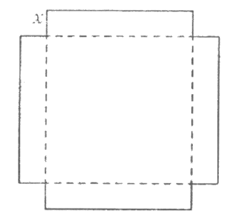
In the figure above, a square with sides of length x inches has been removed from each of the four corners of a square piece of cardboard that originally had an area of 144 square inches. When the cardboard is folded upward along the dashed lines, it forms an open box with no top. Which of the following quantities is represented by (12-2x)2 square inches?
A. The area of the bottom face of the box
B. The area of the five faces of the box
C. The area of the four squares that have been removed from the box
D. The surface area of the closed box
15. Which of the following examples, would exhibit linear growth over time?
A. The height of a plant that doubles in height every two months
B. The value of a home that is increasing in value by 5% every year
C. The number of books read by someone who reads 3 books every month
D. The number of birds in an area where the population of birds is decreasing by 30% every year
16. Which of the following is equivalent to tan(x︒)?
A. 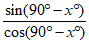
B. 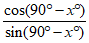
C. 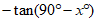
D. 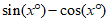
17. In June, 20 people enrolled in a cooking class. In July, the number of people who enrolled increased 150%. How many people enrolled in the cooking class in July?
A. 30 B. 50 C. 70 D. 170
18.
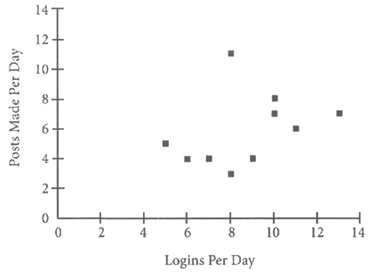
Given the scatterplot graph above, ten students at Welton Academy were polled at random about their usage of the school’s new physics-centered social media app, E=MC Shared. The app was developed to encourage students to discuss physics curricula and concepts in ways that mirrored social media trends in 2013. Students were asked how many times they logged into the app each day as well as how many posts they actually made using the app. With the given data, what conclusions can be drawn about this group of students?
A. The majority of students polled logged in more times per day than they posted.
B. The majority of students polled posted more times per day than they logged in.
C. The majority of students polled logged in and posted an equal number of times.
D. No relationship can be drawn between logins per day and posts per day.
19.
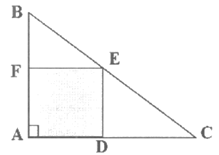
Note:Figure not drawn to scale
In the figure above,ABC is a right triangle and 2AC=3AB. If the quadrilateral AFED is a square,the area of the shaded region is what fraction of the area of triangle ABC?
A. 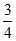 B.
B. 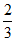 C.
C. 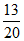 D.
D.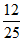
20. In △ ABC and △ DEF, AC=DF and BC=EF. Which of the following additional information is NOT sufficient to prove that △ ABC is congruent to △ DEF?
A. AB=DE
B. m∠CAB=m∠FDE
C. m∠ACB=m∠DFE
D. AB+BC=DE+EF
二、填空题:本大题共5小题,每小题2分,共10分。
21. In the xy -plane, the circle with radius 5 and center (8,3) contains the point (w,0). what is one possible value of w ?
22.
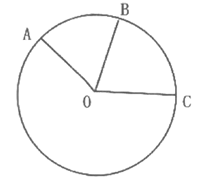
In the circle above, radius 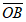 has length 1. The measure of ∠AOB is equal to the measure of ∠BOC, and the length of arc ABC is
has length 1. The measure of ∠AOB is equal to the measure of ∠BOC, and the length of arc ABC is 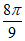 . What is the measure, in degrees, of ∠AOB? (Disregard the degree symbol when gridding your answer.)
. What is the measure, in degrees, of ∠AOB? (Disregard the degree symbol when gridding your answer.)
23. Given that the equation 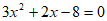 has two distinct solutions, what is the value of the smaller solution subtracted from the larger solution?
has two distinct solutions, what is the value of the smaller solution subtracted from the larger solution?
24. In a circle with center O, central angle AOB has a measure of 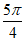 radians. The area of the sector formed by central angle AOB is what fraction of the area of the circle?
radians. The area of the sector formed by central angle AOB is what fraction of the area of the circle?
25.
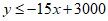
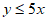
In the xy-plane, if a point with coordinates (a, b) lies in the solution set of the system of inequalities above, what is the maximum possible value of b ?
参考答案
1 | 2 | 3 | 4 | 5 |
D | A | B | C | A |
6. 39 7. 13 8. 3·2n-1
9. 120 10. an=2n+10
11. an=2n-1或an=4·(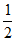 )n-1 12. (1)an=2n-1 (2)Sn=n2+
)n-1 12. (1)an=2n-1 (2)Sn=n2+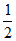 ·(3n-1)
·(3n-1)
第二部分:SAT数学(50分)
一、选择题:本大题共20小题,每小题2分,共40分。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A | A | D | D | A | C | C | C | C | C |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
D | C | A | A | C | B | B | A | D | B |
二、填空题:本大题共5小题,每小题2分,共10分。
21. 4或12(写一个答案就行) 22. 80 23. 10/3
24. 5/8 25. 750
