本试卷满分150分,考试时间120分钟。
一、选择题:共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 集合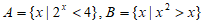 ,则
,则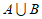 =( )
=( )
A. 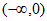 B.
B. 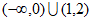 C.
C. 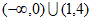 D. R
D. R
2. 在复平面内,复数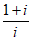 对应的点在( )
对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
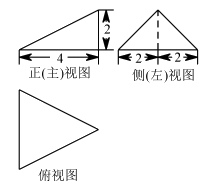
3. 某三棱锥的三视图如图所示,则该三棱锥的体积是( )
A. 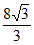 B.
B. 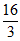 C.
C. 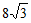 D. 16
D. 16
4. 函数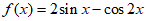 在区间
在区间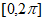 上的零点个数为( )
上的零点个数为( )
A. 2 B. 3 C. 4 D. 5
5. 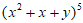 的展开式中,
的展开式中,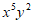 的系数为( )
的系数为( )
A. 10 B. 20 C. 30 D. 60
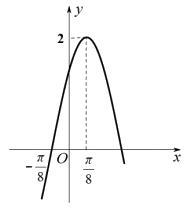
6. 如图是函数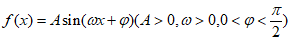 的部分图象,将函数
的部分图象,将函数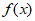 的图象向右平移
的图象向右平移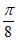 个单位长度得到函数
个单位长度得到函数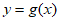 的图象,则下列命题正确的是( )
的图象,则下列命题正确的是( )
A. 函数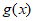 为偶函数
为偶函数
B. 函数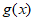 的图象的对称轴是直线
的图象的对称轴是直线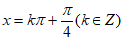
C. 函数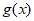 的单调递增区间是
的单调递增区间是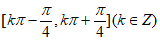
D. 函数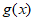 的图象的对称中心是
的图象的对称中心是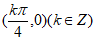
7. 设F为双曲线C: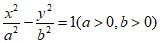 的右焦点,O为坐标原点,以OF为直径的圆与圆
的右焦点,O为坐标原点,以OF为直径的圆与圆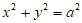 交于P,Q两点,若
交于P,Q两点,若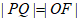 ,则C的离心率为( )
,则C的离心率为( )
A. 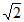 B.
B. 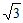 C. 2 D.
C. 2 D.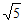
8. 已知圆C: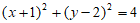 ,若在圆C中存在弦AB,且满足
,若在圆C中存在弦AB,且满足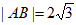 ,且AB的中点在直线
,且AB的中点在直线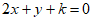 上,则实数k的取值范围是( )
上,则实数k的取值范围是( )
A. 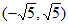 B.
B. 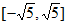 C.
C. 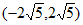 D.
D.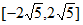
9. 已知数列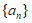 共有6项,其中
共有6项,其中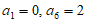 ,且
,且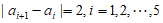 ,则满足条件的不同数列有( )
,则满足条件的不同数列有( )
A. 6个 B. 8个 C. 10个 D. 12个
10. 0-1周期序列在通信技术中有着重要应用,若序列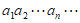 满足
满足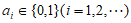 ,且存在正整数m,使得
,且存在正整数m,使得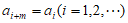 成立,则称其为
成立,则称其为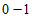 周期序列,并称满足
周期序列,并称满足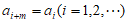 的最小正整数m为这个序列的周期,对于周期为m的
的最小正整数m为这个序列的周期,对于周期为m的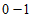 序列
序列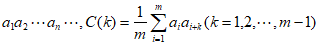 是描述其性质的重要指标,下列周期为5的
是描述其性质的重要指标,下列周期为5的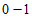 序列中,满足
序列中,满足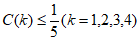 的序列是( )
的序列是( )
A. 11010… B. 11011… C. 10001… D. 11001…
二、填空题:共5小题,每小题5分,共25分。
11. 在边长为2的正三角形ABC中,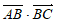 =_____________。
=_____________。
12. 设数列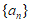 的前n项和为
的前n项和为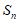 ,若
,若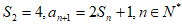 ,则
,则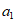 =___________,
=___________,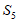 =_____________。
=_____________。
13. 已知函数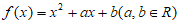 的值域为
的值域为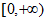 ,若关于x的不等式
,若关于x的不等式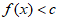 的解集为
的解集为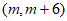 ,则实数c的值为____________。
,则实数c的值为____________。
14. 已知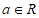 ,函数
,函数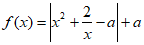 在区间
在区间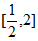 上的最大值为5,则实数a的取值范围是____________。
上的最大值为5,则实数a的取值范围是____________。
15. 在三棱锥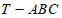 中,
中,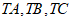 两两垂直,点T在平面ABC上的射影为D,O为三棱锥
两两垂直,点T在平面ABC上的射影为D,O为三棱锥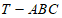 内任意一点,连接
内任意一点,连接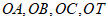 并延长,交对面于点
并延长,交对面于点 ,则下列结论中正确结论的序号是____________。
,则下列结论中正确结论的序号是____________。
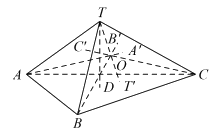
①TA⊥BC,TB⊥AC,TC⊥AB;
②△ABC是锐角三角形;
③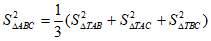 ;
;
④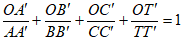 ;
;
⑤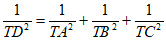 。
。
三、解答题:共6小题,共85分。解答应写出文字说明、演算步骤或证明过程。
16. 本小题13分。设△ABC的内角A,B,C所对的边分别为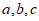 ,且
,且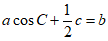 。
。
(1)求角A的大小;
(2)从下面两个条件中任选一个,完成本题的解答。
①若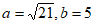 ,求c的值;
,求c的值;
②若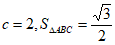 ,求a的值。
,求a的值。
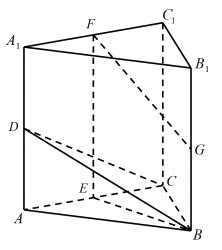
17. 本小题13分。如图,在三棱柱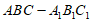 中,
中,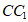 ⊥平面
⊥平面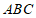 ,
,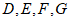 分别为
分别为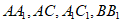 的中点,
的中点,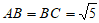 ,
,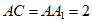 。
。
(1)求证:AC⊥平面BEF;
(2)求二面角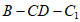 的余弦值。
的余弦值。
18. (本小题14分)盒中有4个球,其中1个红球,1个绿球,2个黄球,从盒中随机取球。每次取1个,不放回,直到取出红球为止,设此过程中取到黄球的个数为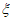 。
。
(1)求取球结束时,没有取到黄球的概率;
(2)求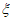 的概率分布列,并求其数学期望
的概率分布列,并求其数学期望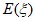 。
。
19. (本小题15分)椭圆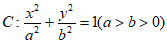 过点
过点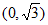 ,其离心率为
,其离心率为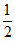 ,椭圆C的左、右焦点分别为
,椭圆C的左、右焦点分别为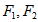 ,过左焦点
,过左焦点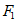 作直线
作直线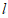 交椭圆于A,B两点。
交椭圆于A,B两点。
(1)求椭圆C的标准方程;
(2)求△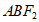 的内切圆半径的最大值。(附:三角形内切圆半径为该三角形面积的2倍除以周长)
的内切圆半径的最大值。(附:三角形内切圆半径为该三角形面积的2倍除以周长)
20. 已知函数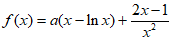 。
。
(1)当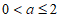 时,讨论函数
时,讨论函数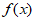 的单调性;
的单调性;
(2)当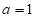 时,令
时,令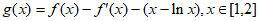 ,试证明
,试证明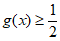 。
。
21. 在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)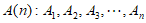 与
与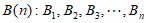 ,其中
,其中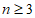 ,若同时满足:
,若同时满足:
①两点列的起点和终点分别相同;②线段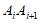 ⊥
⊥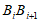 ,其中
,其中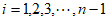 ,则称
,则称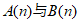 互为正交点列。
互为正交点列。
(1)求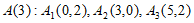 的正交点列
的正交点列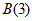 ;
;
(2)判断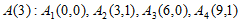 是否存在正交点列
是否存在正交点列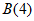 ?并说明理由;
?并说明理由;
(3)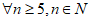 ,是否都存在无正交点列的有序整点列
,是否都存在无正交点列的有序整点列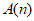 ?并证明你的结论。
?并证明你的结论。
【试题答案】
一、选择题
1. D 2. D
3. B
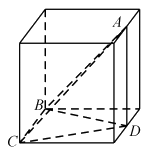
由三视图在长方体中作出三棱锥的直观图,如图所示,
则该三棱锥的体积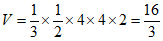 。
。
4. A
5. C
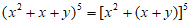 的通项公式为
的通项公式为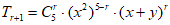 ,又
,又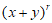 的通项公式为
的通项公式为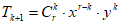 ,所以
,所以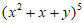 的通项公式为
的通项公式为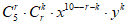 (
(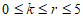 ),令
),令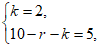 得
得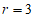 ,所以
,所以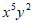 的系数为
的系数为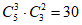 。
。
6. C 7. A 8. B 9. C 10. C
二、填空题
11. -2
12. 1;121
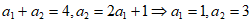 ,
,
再由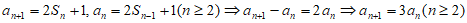 ,
,
又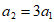 ,
,
所以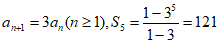 。
。
13. 9
14. 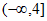
15. ①②④⑤
16. (1)由正弦定理即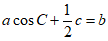 得
得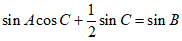 ,
,
化简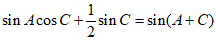 ,解得
,解得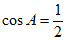 ,
,
因为0°<A<180°,
所以A=60°。
(2)选①:由余弦定理得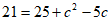 ,即
,即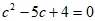 ,
,
解得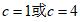 。
。
经验证1,4都是解,所以c的值是1或4。
选②:由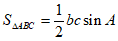 ,得到
,得到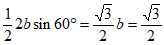 ,所以
,所以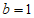 ,再由余弦定理,
,再由余弦定理,
得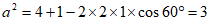 ,所以
,所以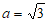 。
。
17. (1)三棱柱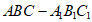 中,
中,
因为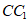 ⊥平面ABC,
⊥平面ABC,
所以四边形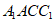 为矩形。
为矩形。
又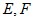 分别为
分别为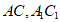 的中点,
的中点,
所以AC⊥EF,
因为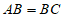 ,
,
所以AC⊥BE,
所以AC⊥平面BEF。
(2)由(1)知AC⊥EF,AC⊥BE,EF∥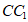 ,
,
又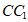 ⊥平面ABC,
⊥平面ABC,
所以EF⊥平面ABC,
因为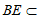 平面ABC,
平面ABC,
所以EF⊥BE。
如图建立空间直角坐标系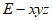 。
。
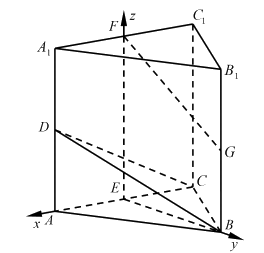
由题意得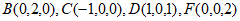 ,
,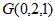 ,
,
所以 。
。
设平面BCD的法向量为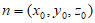 ,则
,则
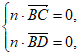 即
即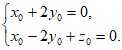
令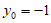 ,则
,则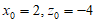 ,
,
于是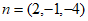 。
。
又因为平面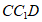 的法向量为
的法向量为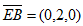 ,
,
所以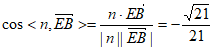 。
。
由题知二面角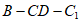 为钝角,所以其余弦值为
为钝角,所以其余弦值为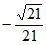 。
。
18. 我们用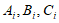 分别表示第i次取到红球,绿球,黄球的事件,
分别表示第i次取到红球,绿球,黄球的事件,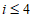 。
。
(1)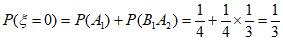 。
。
(2)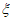 可以取
可以取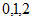 ,
,
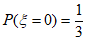 ,
,
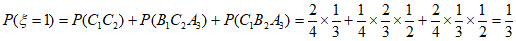 ,
,
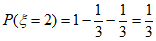 。
。
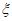 的概率分布列为:
的概率分布列为:
| 0 | 1 | 2 |
P |
|
|
|
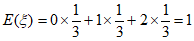 。
。
19. (1)因为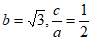 ,所以
,所以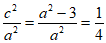 ,所以
,所以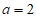 ,
,
则椭圆的标准方程为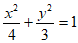 。
。
(2)当直线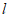 斜率为零时,△
斜率为零时,△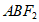 不存在,设直线
不存在,设直线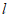 的方程为
的方程为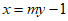 ,
,
由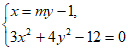 得
得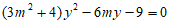 。
。
设点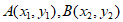 ,则有
,则有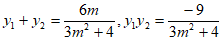 ,
,
设△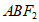 的内切圆半径为r,
的内切圆半径为r,
则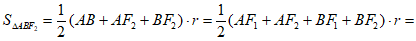
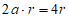 ,
,
所以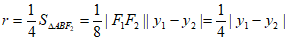 。
。
因为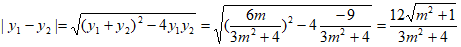 ,
,
所以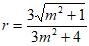 。
。
设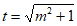 ,则
,则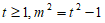 ,内切圆半径
,内切圆半径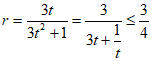 ,等号当且仅当
,等号当且仅当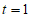 时取得,
时取得,
所以△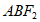 的内切圆半径的最大值为
的内切圆半径的最大值为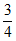 。
。
20. (1)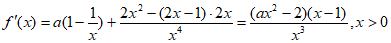 。
。
①当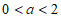 时,
时,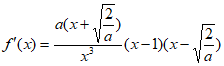 ,
,
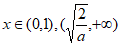 时,
时,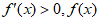 单调增;
单调增;
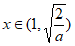 时,
时,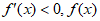 单调减,
单调减,
所以函数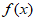 的单调递增区间是
的单调递增区间是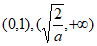 ,单调递减区间是
,单调递减区间是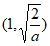 。
。
②当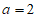 时,
时,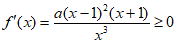 ,所以函数
,所以函数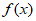 的单调递增区间是
的单调递增区间是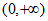 。
。
(2)当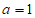 时,
时,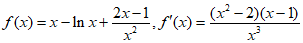
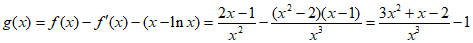 ,
,
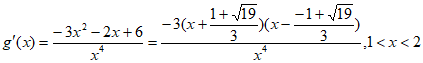 ,
,
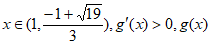 单调增;
单调增;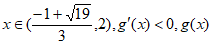 单调减,
单调减,
所以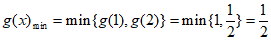 ,所以
,所以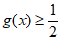 。
。
21. (1)设点列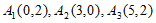 的正交点列是
的正交点列是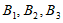 ,
,
由正交点列的定义可知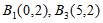 ,设
,设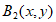 ,
,
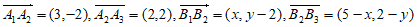 ,
,
由正交点列的定义可知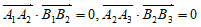 ,
,
即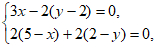 解得
解得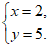
所以点列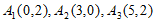 的正交点列是
的正交点列是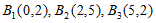 。
。
(2)由题可得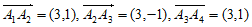 ,
,
设点列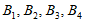 是点列
是点列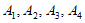 的正交点列,
的正交点列,
则可设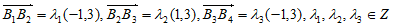 ,
,
因为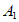 与
与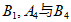 相同,所以有
相同,所以有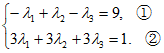
因为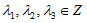 ,方程②显然不成立,
,方程②显然不成立,
所以有序整点列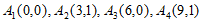 不存在正交点列。
不存在正交点列。
(3)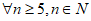 ,都存在整点列
,都存在整点列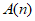 无正交点列,
无正交点列,
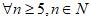 ,设
,设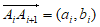 ,其中
,其中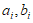 是一对互质整数,
是一对互质整数,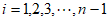 ,
,
若有序整点列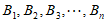 是点列
是点列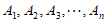 正交点列,
正交点列,
则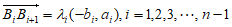 ,
,
则有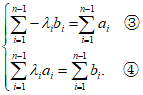
当n为偶数时,
取 ,
,
由于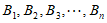 是整点列,所以有
是整点列,所以有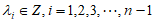 ,
,
等式④中左边是3的倍数,右边等于1,等式不成立,
所以该点列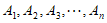 无正交点列;
无正交点列;
当n为奇数时,
取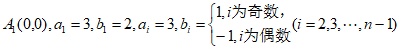 ,
,
由于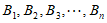 是整点列,所以有
是整点列,所以有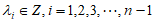 ,
,
等式④中左边是3的倍数,右边等于1,等式不成立,
所以该点列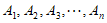 无正交点列。
无正交点列。
综上所述,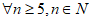 ,都存在无正交点列的有序整数点列
,都存在无正交点列的有序整数点列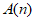 。
。